2  Die R Sprache

2.1 Operatoren und Funktionen

Als erste Anwendung können wir R als Taschenrechner benützen. Zuvor müssen wir uns aber noch ein wenig Vokabular aneignen, und dann ein bisschen Syntax lernen.

Zum Basisvokabular gehören einige eingebaute Operatoren (sowohl arithmetische als auch logische).

2.1.1 Arithmetische Operatoren

Die ersten fünf Operatoren sollten selbsterklärend sein:

+                Addition
-                Subtraktion
*                Multiplikation
/                Division
^ oder **        Potenz

x %*% y          Matrixmultiplikation c(5, 3) %*% c(2, 4) == 22
x %% y           Modulo (x mod y) 5 %% 2 == 1
x %/% y          Ganzzahlige Teilung: 5 %/% 2 == 2
Hinweis

Die letzten drei Operatoren sind vielleicht nicht allen geläufig. %*% ist der Operator für die Matrixmultiplikation. Der einfachste Fall ist die Multiplikation zweier gleich langer Vektoren (eines Zeilen- und eines Spaltenvektors). Dabei werden die Elemente der beiden Vektoren elementweise miteinander multipliziert und anschliessend die Produkte aufsummiert. Ergebnis ist ein Skalar (eine einzelne Zahl bzw. ein Vektor mit nur einem Element), z.B. c(5, 3) %*% c(2, 4) ergibt 22 (5*2 + 3*4). %% ist der Modulo Operator und gibt den Rest nach einer ganzzahligen Division an. So gibt z.B. 5 %% 2 (sprich 5 modulo 2) den Wert 1. %/% gibt das Resultat der ganzzahligen Division, d.h. 5 %/% 2 gibt den Wert 2 (wie oft kann man 2 von 5 subtrahieren?). Diese Operatoren werden beim Programmieren oft gebraucht, spielen in diesem Einführungskurs aber nur eine untergeordnete Rolle.

2.1.2 Logische Operatoren und Funktionen

Die letzten beiden Funktionen, xor() und isTRUE(), werden Sie wahrscheinlich selten brauchen, sie sind nur der Vollständigkeit halber aufgelistet.

<                Kleiner
<=               Kleiner gleich
>                Grösser
>=               Grösser gleich
==               Gleich (testet auf Äquivalenz)
!=               Ungleich
!x               Nicht x (Verneinung)
x | y            x ODER y
x & y            x UND y

xor(x, y)        Exklusives ODER (entweder in x oder y, aber nicht in beiden)
isTRUE(x)        testet ob x wahr ist

Die folgende Grafik zeigt die Verwendung der logischen Operatoren anhand von Venn-Diagrammen. x bezieht sich dabei immer den linken Kreis, y auf den rechten. Der ausgewählte Bereich ist immer dunkel dargestellt.

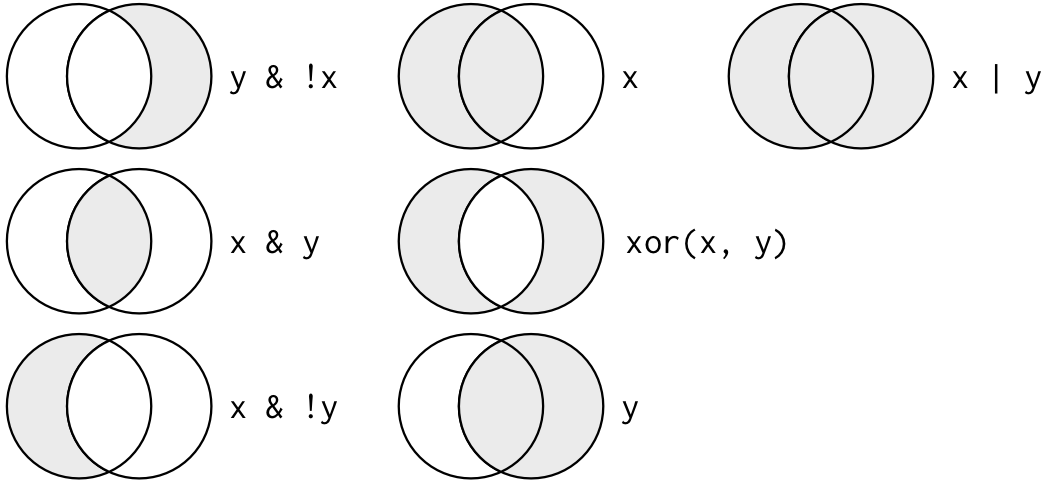
Veranschaulichung der logischen Operatoren. Aus R for Data Science (Wickham & Grolemund, 2017).

Es kommen noch weitere numerische Funktionen hinzu. Diese werden jedoch als Funktionen gebraucht, und nicht als Operatoren.

Hinweis

Operatoren werden so gebraucht: 1 + 2 (sie stehen zwischen den Operanden). Funktionen sehen so aus: abs(x) (sie werden auf Argumente angewendet).

2.1.3 Numerische Funktionen

abs(x)             Betrag
sqrt(x)            Quadratwurzel
ceiling(x)         Aufrunden: ceiling(3.475) ist 4
floor(x)           Abrunden: floor(3.475) ist 3
round(x, digits = n) Runden: round(3.475, digits = 2) ist 3.48
log(x)             Natürlicher Logarithmus
log(x, base = n)   Logarithmus zur Basis n
log2(x)            Logarithmus zur Basis 2
log10(x)           Logarithmus zur Basis 10
exp(x)             Exponentialfunktion: e^x
Vertiefung

Es gibt in R streng genommen keinen Unterschied zwischen Operatoren und Funktionen. Jeder Operator ist eigentlich eine Funktion mit einer speziellen Infix-Notation. So kann z.B. der Operator + auch als Funktion benützt werden, allerdings muss dieser dann mit ` ` (backticks) umgeben werden. Sie können dies in der Konsole ausprobieren.

# Als Operator mit Infix Notation
2 + 3 
[1] 5
# Als Funktionsaufruf
`+`(2, 3)
[1] 5
# Die beiden Schreibweisen sind äquivalent
2 + 3 == `+`(2, 3)
[1] TRUE

2.1.4 R als Taschenrechner

Wir können nun mit R rechnen. Im nächsten Code-Chunk sehen Sie einige Beispiele. R verwendet den hash key # als Kommentarzeichen, d.h. Zeilen, welche mit einem # beginnen, werden nicht evaluiert, und werden dazu benützt, den Code zu kommentieren.

Führen Sie diese Befehle aus, in dem Sie die einzelnen Zeilen auswählen, und dann gleichzeitig die CMD + Enter (macOS) oder CTRL + Enter (Windows) Tasten drücken.

# Addition
5 + 5
[1] 10
99 + 89
[1] 188
12321 + 34324324
[1] 34336645
# Subtraktion
6 - 5
[1] 1
5 - 89
[1] -84
# Multiplikation
3 * 5
[1] 15
34 * 54
[1] 1836
# Division
4 / 9
[1] 0.4444444
(5 + 5) / 2
[1] 5
# Operatorpräzedenz: Klammern beachten
# Punktrechnung vor Strichrechnung

(3 + 7 + 2 + 8) / (4 + 11 + 3)
[1] 1.111111
1/2 * (12 + 14 + 10)
[1] 18
1/2 * 12 + 14 + 10
[1] 30
# Potenzieren
3^2
[1] 9
2^12
[1] 4096
# Exponententialfunktion
exp(5)
[1] 148.4132
# Das nächste Resultat ist so gross,
# dass es in wissenschaftlicher Notation erscheint:
# 1.068647 * 10^13
exp(30)
[1] 1.068647e+13
# Ganzzahlige Division
# 28 ist vier mal durch 6 teilbar, mit Rest 4 
28 %% 6 # Rest: 4
[1] 4
28 %/% 6 #  vier mal teilbar
[1] 4
5 %% 2 # Rest: 1
[1] 1
5 %/% 2 # zwei mal teilbar
[1] 2
# Logische Operatoren
3 > 2
[1] TRUE
4 > 5
[1] FALSE
4 < 4
[1] FALSE
4 <= 4
[1] TRUE
5 >= 5
[1] TRUE
6 != 6
[1] FALSE
9 == 5 + 4
[1] TRUE
!(3 > 2)
[1] FALSE
(3 > 2) & (4 > 5) # UND
[1] FALSE
(3 > 2) | (4 > 5) # ODER
[1] TRUE
xor((3 > 2), (4 > 5))
[1] TRUE
Hinweis

Bei xor darf nur entweder der eine oder der andere Ausdruck wahr sein, damit der gesamte Ausdruck wahr ist (exklusives ODER, ausschliessende Disjunktion), während bei | mindestens einer der Ausdrücke wahr sein muss, damit der Gesamtausdruck wahr ist (inklusives ODER, nicht-ausschliessende Disjunktion). Während also (3 > 2) | (4 > 5) und xor((3 > 2), (4 > 5)) beide TRUE ergeben, ergibt (3 > 2) | (5 > 4) TRUE, aber xor((3 > 2), (5 > 4)) ergibt FALSE.

Übung

Berechnen Sie:

  1. \(\frac{1}{3} \cdot \frac{1+3+5+7+2}{3 + 5 + 4}\)

  2. \(e\) (wie lässt sich das berechnen?)

  3. \(\sqrt{2}\)

  4. \(\sqrt[3]{8}\)

  5. \(log_2(8)\)

(1/3) * (1 + 3 + 5 + 7 + 2) / (3 + 5 + 4)
[1] 0.5
exp(1)
[1] 2.718282
sqrt(2)
[1] 1.414214
8^(1/3)
[1] 2
log(8, base = 2)
[1] 3
log2(8)
[1] 3

2.1.5 Statistische Funktionen

Hier ist eine Auflistung statistischer Funktionen, die alle auf einen Vektor angewendet werden können (z.B. zur Berechnung des arithmetischen Mittels einer Messwertreihe). Diese Funktionen haben alle das Argument na.rm, welches standardmässig den Wert FALSE annimmt. Das bedeutet, dass mögliche fehlende Werte (na = not available) in diesem Fall nicht entfernt (rm = remove) werden, bevor die Funktion ausgeführt wird. Das führt allerdings dazu, dass diese Funktionen im Falle vorhandener NAs selbst das Ergebnis NA liefern, da sie nicht auf fehlende Werte angewendet werden können (vgl. Beispiel unten). Es empfiehlt sich daher, diese Funktionen mit dem Argument na.rm = TRUE zu verwenden. So werden fehlende Werte vor Anwendung einer Funktion entfernt, und die Funktion somit nur auf gültige Werte angewendet. Am besten ergänzt man solche Funktionen zur Berechnung des Mittelwerts, der Varianz etc. durch eine Funktion zur Zählung der fehlenden Werte in einem Vektor, da sonst nicht klar ist, wie gross die Zahl/der Anteil gültiger Werte bei der Berechnung der Statistik war. Darauf werden wir weiter unten zurückkommen.

mean(x, na.rm = FALSE)  Mittelwert
sd(x)                   Standardabweichung
var(x)                  Varianz

median(x)               Median
quantile(x, probs)      Quantile von x.  probs: Vektor mit Wahrscheinlichkeiten

sum(x)                  Summe
min(x)                  Minimalwert x_min
max(x)                  Maximalwert x_max
range(x)                x_min und x_max

2.1.6 Zentrieren und standardisieren mit scale()

Mit der Funktion scale() kann ein Vektor, d.h. eine Reihe von Messwerten zentriert oder z-standardisiert werden. Bei der Zentrierung (Argument: center = TRUE) wird ein Vektor mit Abweichungswerten vom Mittelwert ausgegeben, bei der z-Standardisierung (mit dem zusätzlichen Argument: scale = TRUE) werden die Abweichungswerte noch durch die Stichprobenstandardabweichung geteilt, so dass standardisierte Werte entstehen.

Da center = TRUE und scale = TRUE die Default-Einstellungen der Funktion scale() sind, berechnet die Funktion ohne explizite Angabe der Argumente z-standardisierte Werte. Wenn man nur zentrieren will, muss scale = FALSE gesetzt werden. Wenn man (in seltenen Fällen) die ursprünglichen Werte durch die Standardabweichung teilen will, aber ohne vorherige Zentrierung, muss center = FALSE gesetzt werden.

# wenn center = TRUE: zentrieren
# wenn scale = TRUE: durch SD teilen
scale(x, center = TRUE, scale = FALSE)  Zentrieren
scale(x, center = TRUE, scale = TRUE)   Standardisieren (Default-Einstellung)

2.1.7 Ziehen einer Zufallsstichprobe mit sample()

Mit der Funktion sample() kann eine (Pseudo-)Zufallsstichprobe von Werten/Elementen aus dem Vektor x (Datenargument, “Urne”) der Grösse size gezogen werden, und zwar “mit Zurücklegen” (replace = TRUE) oder “ohne Zurücklegen” (replace = FALSE, default). Ohne Angabe des Argumentes prob werden alle Elemente aus x mit gleicher Wahrscheinlichkeit gezogen. Wenn gewichtet gezogen werden soll, muss in prob ein Vektor mit Wahrscheinlichkeiten für jedes Element in x definiert werden. Statt Wahrscheinlichkeiten, die sich zu 1 addieren, können auch Zahlen verwendet werden, die die Verhältnisse “der Kugeln in der Urne” widerspiegeln. Mit anderen Worten: sample() rechnet die in prob angegebenen Werte automatisch in Wahrscheinlichkeiten um. Um keine Fehler zu machen, empfiehlt es sich aber, die Wahrscheinlichkeiten immer explizit anzugeben.

Wichtig: Beim Ziehen ohne Zurücklegen (replace = FALSE) darf die in size angegebene Grösse der Zufallsstichprobe nicht grösser sein als die Anzahl der in x enthaltenen Elemente. Wenn size und length(x) genau gleich gross sind, ist das Ergebnis von sample() eine zufällige Permutation der Elemente in x.

Tipp: Wenn man das Ergebnis einer Zufallsziehung reproduzierbar machen will, muss vor Ausführung von sample() mit der Funktion set.seed() ein beliebiger Startwert (z.B. 123 oder 5983467) angegeben werden. Wird vor der nächsten Durchführung der (gleichen) Zufallsziehung derselbe Startwert wieder gesetzt, erhält man wieder dasselbe Ergebnis. Daran kann man erkennen, dass hinter der Funktion sample() kein wahrer Zufallsvorgang steckt, sondern damit ein komplizierter Algorithmus in Gang gesetzt wird, der einen Zufallsvorgang simuliert (und der - wenn man am selben Punkt “einsteigt” - immer zum selben, nichtzufälligen Ergebnis kommt).

sample(x, size, replace, prob)  Ziehen mit/ohne Zurücklegen. 
prob: Vektor mit Wahrscheinlichkeiten

2.1.8 Weitere nützliche Funktionen

c()                    Combine: kreiert einen Vektor
seq(from, to, by)      Generiert eine Sequenz
:                      Colon Operator: generiert eine reguläre Sequenz 
                       (d.h. Sequenz in Einerschritten)
rep(x, times, each)    Wiederholt x
                       times: die Sequenz wird n-mal wiederholt
                       each: jedes Element wird n-mal wiederholt

head(x, n = 6)         Zeigt die n ersten Elemente von x an
tail(x, n = 6)         Zeigt die n letzten Elemente von x an

2.1.9 Beispiele

c(1, 2, 3, 4, 5, 6)
[1] 1 2 3 4 5 6
mean(c(1, 2, 3, 4, 5, 6))
[1] 3.5
mean(c(1, NA, 3, 4, 5, 6), na.rm = TRUE)
[1] 3.8
mean(c(1, NA, 3, 4, 5, 6), na.rm = FALSE)
[1] NA
sd(c(1, 2, 3, 4, 5, 6))
[1] 1.870829
sum(c(1, 2, 3, 4, 5, 6))
[1] 21
min(c(1, 2, 3, 4, 5, 6))
[1] 1
range(c(1, 2, 3, 4, 5, 6))
[1] 1 6
scale(c(1, 2, 3, 4, 5, 6), center = TRUE, scale = FALSE)
     [,1]
[1,] -2.5
[2,] -1.5
[3,] -0.5
[4,]  0.5
[5,]  1.5
[6,]  2.5
attr(,"scaled:center")
[1] 3.5
# Der Mittelwert des zentrierten Vektors wird zur Information mit ausgegeben!
scale(c(1, 2, 3, 4, 5, 6), center = TRUE, scale = TRUE)
           [,1]
[1,] -1.3363062
[2,] -0.8017837
[3,] -0.2672612
[4,]  0.2672612
[5,]  0.8017837
[6,]  1.3363062
attr(,"scaled:center")
[1] 3.5
attr(,"scaled:scale")
[1] 1.870829
# Mittelwert und Standardabweichung des z-standardisierten Vektors 
# werden zur Information mit ausgegeben!
# Ziehen mit Zurücklegen
sample(c(1, 2, 3, 4, 5, 6), size = 1, replace = TRUE)
[1] 4
sample(c(1, 2, 3, 4, 5, 6), size = 12, replace = TRUE)
 [1] 2 4 3 5 4 5 6 4 5 1 3 6
# Ziehen mit Zurücklegen, ungleich gewichtet:
sample(c(1, 2, 3, 4, 5, 6), size = 1, replace = TRUE,
       prob = c(4/12, 1/12, 1/12, 2/12, 2/12, 2/12 ))
[1] 4
sample(c(1, 2, 3, 4, 5, 6), size = 12, replace = TRUE,
       prob = c(4/12, 1/12, 1/12, 2/12, 2/12, 2/12 ))
 [1] 4 3 5 1 6 1 1 1 2 2 4 4
c(1, 2, 3, 4, 5, 6)
[1] 1 2 3 4 5 6
seq(from = 1, to = 6, by = 1)
[1] 1 2 3 4 5 6
1:6
[1] 1 2 3 4 5 6
rep(1:6, times = 2)
 [1] 1 2 3 4 5 6 1 2 3 4 5 6
rep(1:6, each = 2)
 [1] 1 1 2 2 3 3 4 4 5 5 6 6
rep(1:6, times = 2, each = 2)
 [1] 1 1 2 2 3 3 4 4 5 5 6 6 1 1 2 2 3 3 4 4 5 5 6 6
Übung
  1. Erzeugen Sie eine Sequenz von 0 bis 100 in 5-er Schritten.
  2. Berechnen Sie den Mittelwert des Vektors [1, 3, 4, 7, 11, 2].
  3. Lassen Sie sich die Spannweite \(x_{max} - x_{min}\) dieses Vektors ausgeben.
  4. Berechnen Sie die Summe dieses Vektors.
  5. Zentrieren Sie diesen Vektor.
  6. Simulieren Sie einen Münzwurf mit der Funktion sample(). Tipp: nehmen Sie für Kopf 1 und für Zahl 0. Simulieren Sie 100 Münzwürfe.
  7. Simulieren Sie eine Trick-Münze mit \(p \neq 0.5\)
  8. Generieren Sie einen Vektor, der aus 100 Wiederholungen der Zahl 3 besteht.
# 1)
seq(0, 100, by = 5)
 [1]   0   5  10  15  20  25  30  35  40  45  50  55  60  65  70  75  80  85  90
[20]  95 100
# 2)
c(1, 3, 4, 7, 11, 2)
[1]  1  3  4  7 11  2
mean(c(1, 3, 4, 7, 11, 2))
[1] 4.666667
# 3)
max(c(1, 3, 4, 7, 11, 2)) - min(c(1, 3, 4, 7, 11, 2))
[1] 10
# 4)
sum(c(1, 3, 4, 7, 11, 2))
[1] 28
#  5) Zentrieren
scale(c(1, 3, 4, 7, 11, 2), scale = FALSE)
           [,1]
[1,] -3.6666667
[2,] -1.6666667
[3,] -0.6666667
[4,]  2.3333333
[5,]  6.3333333
[6,] -2.6666667
attr(,"scaled:center")
[1] 4.666667
# 6)
sample(c(1, 0), size = 1, replace = TRUE)
[1] 1
sample(c(1, 0), size = 100, replace = TRUE)
  [1] 0 1 1 1 1 1 0 0 0 1 1 0 0 0 1 0 0 1 0 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 1 1
 [38] 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0
 [75] 1 0 1 1 0 0 0 1 1 0 1 1 0 0 1 1 1 1 0 0 1 1 0 1 1 0
# 7) Trick coin
sample(c(1, 0), size = 100, replace = TRUE, prob = c(5/6, 1/6))
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 0 0 1 0 0 1 1 1 1 1
 [38] 1 1 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1
 [75] 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0
# 8) 
rep(3, times = 100)
  [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
 [38] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
 [75] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3

2.2 Variable definieren

Bisher haben wir die Resultate unserer Berechnungen nicht gespeichert. Selbstverständlich können wir in R Variablen definieren, und diesen einen oder mehrere Werte zuweisen. Allgemeiner sprechen wir von der Zuweisung bzw. Definition von “Objekten”.

Variablen bzw. Objekte werden in R so definiert: my_var <- 4. <- ist hier ein spezieller Zuweisungspfeil, und besteht aus einem < Zeichen und einem -. Es gibt in RStudio dafür eine Tastenkombination ALT + - (auf dem Mac option + -). Hier weisen wir also der neuen Variablen my_var den Wert 4 zu.

Vertiefung

Man kann in R sowohl <- als auch = als Zuweisungsoperator verwenden. Auf den ersten Blick erscheint das verwirrend (es ist aus historischen Gründen so). Da = ausserdem das Symbol für die Zuweisung von Argumenten (in Funktionen) ist, empfehlen wir für die Zuweisung von Variablen/Objekten den Zuweisungspfeil <-: dann ist klar, dass man eine Variable definiert. Ausserdem haben R Puristen <- lieber.

2.2.1 Variablennamen

Eine Variable muss also einen Namen haben - dieser besteht aus Buchstaben, Zahlen und den Zeichen _ und/oder . Ein Variablenname muss mit einem Buchstaben beginnen, und darf keine Leerschläge enthalten.

Es gibt ein paar Konventionen, an die man sich halten sollte, um R Code lesbar und verständlich zu machen - vor allem, wenn man diesen mit anderen teilt. Wir empfehlen, für die Namensgebung snake_case zu verwenden, d.h. wir trennen Wörter innerhalb eines Namens mit einem Unterstrich: my_var.

Hier zusammen mit weiteren Möglichkeiten:

snake_case_variable
camelCaseVariable
variable.with.periods
variable.With_noConventions
# gute Variablennamen
x_mean
x_sd

anzahl_personen
alter

# weniger gute Variablennamen
p
a

# unmögliche Variablennamen
x mittelwert
sd von x

In vielen Texten, vor allem in älteren, findet man Variablennamen mit . anstelle von _, moderne Style Guides empfehlen aber _.

Wenn wir eine Variable definiert haben:

my_var <- 4

können wir uns deren Wert in der Konsole ausgeben lassen:

print(my_var)
[1] 4
# oder einfach

my_var
[1] 4
Vertiefung

Man kann auch gleich bei der Definition der Variablen die Zuweisung in Klammern schreiben, und das Resultat wird gleichzeitig in der Konsole angezeigt:

(my_var <- 4)
[1] 4

Das ist manchmal praktisch, im Allgemeinen definiert man aber zunächst eine Variable/ein Objekt und lässt es sich anschliessend ausgeben (oder auch nicht).

Hinweis

Wenn Sie die Variable my_var definieren, sehen Sie in RStudio im Environment-Bereich eine neue Variable und deren Wert unter Values.

Übung

Wiederholen Sie einige der Beispiele von oben, aber speichern Sie diesmal die Resultate in neuen Variablen ab. Sie können die Variablen dann für weitere Operationen wieder verwenden.

vektor <- c(1, 3, 4, 7, 11, 2)
summe <- sum(vektor)

mittelwert <- mean(vektor)
mittelwert
[1] 4.666667
gerundeter_mittelwert <- round(mittelwert, digits = 1)
gerundeter_mittelwert
[1] 4.7

Diese Variablen existieren nun im Global Environment, aber nur solange die aktuelle R Session bestehen bleibt (die Zuweisung/Erstellung einer Variablen speichert diese also nicht im Wortsinne). Wenn sie R neu starten, sind diese Variablen nicht mehr vorhanden. Deshalb sollte man immer in einem R Script oder R Notebook festhalten, was man gemacht hat.

2.3 Funktionen aufrufen

Wir haben nun schon einige Funktionen verwendet. Hier schauen wir uns nun die Syntax eines Funktionsaufrufs (function call) an.

Die Funktion, welche unten angezeigt wird, besteht aus einem Namen function_name und hat zwei Argumente, arg1 und arg2. Die Argumente können, aber müssen nicht, default (voreingestellte) Werte haben. In diesem Beispiel hat arg1 keinen default Wert. arg2 hat den default Wert val2. Argumente ohne default Werte müssen beim Aufruf einer Funktion zwingend angegeben werden. Wenn man Argumente mit default Werten nicht explizit angibt, wird automatisch der jeweilige default Wert für das Argument verwendet. Typische default Werte für Argumente sind TRUE oder FALSE, z.B. gibt es wie oben bereits beschrieben in vielen Funktionen das Argument na.rm mit der Voreinstellung (default Wert) na.rm = FALSE. Wenn dieses Argument also NICHT explizit angegeben wird, werden fehlende Werte nicht entfernt, bevor die jeweilige Funktion angewendet wird und die Funktion gibt im Fall vorhandener fehlender Werte dann als Ergebnis selbst NA aus.

function_name(arg1, arg2 = val2)

Eine Funktion kann beliebig viele Argumente haben.

Hinweis

Wir verwenden in R den = Operator, wenn wir einem Argument einen Wert zuweisen. Der Unterschied zwischen <- und = ist am Anfang nicht ganz leicht nachvollziehbar, und wird hier noch einmal illustriert.

# Zuweisungspfeil:
# `<-` weist einem Objekt, z.B. einer Variablen, einen (oder mehrere) Wert(e) zu:
x <- c(23.192, 21.454, 24.677)

# Gleichheitszeichen:
# `=` weist bei einem Funktionsaufruf den Argumenten der Funktion einen Wert zu.
# Z.B. die round Funktion:
round(x, digits = 1)
[1] 23.2 21.5 24.7

Das Argument digits bestimmt, auf wieviele Nachkommastellen gerundet werden soll, und wird innerhalb der Funktion round() verwendet. Mit = weisen wir diesem Argument den Wert 1 zu.

Wenn man wissen will, welche Argumente eine Funktion hat, kann man dies am besten mit Tab-Completion herausfinden.

Übung

Tippen Sie in der Konsole scale( und drücken Sie TAB. Sie sehen, dass diese Funktion drei Argumente hat, x, center und scale. Schreiben Sie scale(vektor, scale = gefolgt von TAB. Sie sehen, dass scale = TRUE den default Wert TRUE hat.

Was sind die Argumente der Funktion round()? Hat eines der Argumente einen default Wert?

Schauen Sie im Help Viewer nach, was die Funktion rnorm() macht. Was sind die Argumente. Was bedeuten die default Werte?

Schauen Sie im Help Viewer nach, welche Argumente die seq() Funktion hat.

Was machen folgende Funktionsaufrufe?

seq()
seq(1, 10)
seq(1, 10, 2)
seq(1, 10, 2, 20)
seq(1, 10, length.out = 20)

2.3.1 Verschachtelung von Funktionen

Wir können beliebig viele Funktion ineinander verschachteln, d.h. wir können den Output einer Funktion einer weiteren Funktion als Input übergeben. Wir sehen uns diese Verschachtelung an folgendem Beispiel an.

Wir definieren zuerst einen Vektor, berechnen davon den Mittelwert und runden diesen auf zwei Dezimalstellen:

# definiert einen Vektor:
c(34.444, 45.853, 21.912, 29.261, 31.558)
[1] 34.444 45.853 21.912 29.261 31.558
# berechnet den Mittelwert:
mean(c(34.444, 45.853, 21.912, 29.261, 31.558))
[1] 32.6056
# rundet auf 2 Dezimalstellen:
round(mean(c(34.444, 45.853, 21.912, 29.261, 31.558)),
      digits = 2)
[1] 32.61

Die Funktionen werden immer in der Reihenfolge von innen nach aussen ausgeführt, d.h. zuerst mean(), und dann round().

Wenn wir mehrere Funktionen ineinander verschachteln, kann unser Code schnell unlesbar werden. Natürlich könnten wir die einzelnen Zwischenschritte speichern, wie im Beispiel weiter oben, aber dann definieren wir eine Menge Variablen, welche wir vielleicht gar nicht benötigen. Wir werden im Kapitel über Datentransformation einen neuen Operator kennenlernen, welcher eine sehr elegante Lösung für dieses Problem bietet.

2.4 Datentypen

Wir haben bisher mit Vektoren gearbeitet. Diese stellen den fundamentalen Datentyp dar. Alle weiteren Datentypen bauen auf diesem auf. Vektoren selber können in folgende Typen unterschieden werden in:

  • numeric vectors: Mit diesen hatten wir es bisher zu tun. Numerische Vektoren werden weiter in integer (ganze Zahlen) und double (reelle Zahlen) unterteilt.

  • character vectors: Die Elemente dieses Typs bestehen aus Zeichen, welche von Anführungszeichen umgeben werden (entweder ' oder " ), z.B. 'Wort' oder "Wort".

  • logical vectors: Die Elemente dieses Typs können nur 3 Werte annehmen: TRUE, FALSE oder NA.

Vektoren müssen aus denselben Elementen bestehen, d.h. wir können nicht logical und character Vektoren mischen. Vektoren haben 3 Eigenschaften:

  • Typ: typeof(): Was ist es?
  • Länge: length(): Wie viele Elemente?
  • Attribute: attributes(): Zusätzliche Information (Metadaten)

Vektoren werden entweder mit der c() (Abkürzung für combine) Funktion erstellt, oder mit speziellen Funktion, wie z.B. seq() oder rep(). Wir schauen uns nun die verschiedenen Typen von Vektoren an.

2.4.1 Numeric vectors

Numerische Vektoren bestehen aus Zahlen. Und zwar entweder aus natürlichen Zahlen (integer) oder aus reellen Zahlen (double).

numbers <- c(1, 2.5, 4.5)
typeof(numbers)
[1] "double"
length(numbers)
[1] 3

Wir können die einzelnen Elemente eines Vektor mit [] auswählen (dies nennt man im Fachjargon subsetting):

# Das erste Element:
numbers[1]
[1] 1
# Das zweite Element:
numbers[2]
[1] 2.5
# Das letzte Element:
# numbers hat die Länge 3
length(numbers)
[1] 3
# Wir können damit numbers indizieren
numbers[length(numbers)]
[1] 4.5
# Mit - (Minus) können wir ein Element weglassen, z.B. alle Elemente ausser das Erste:
numbers[-1]
[1] 2.5 4.5
# Wir können eine Sequenz verwenden, z.B. die ersten zwei Elemente:
numbers[1:2]
[1] 1.0 2.5
# Wir können das erste und dritte Element weglassen:
numbers[-c(1, 3)]
[1] 2.5

Matrizen

Wie bereits erwähnt, ist eigentlich alles in R ein Vektor. Ein Skalar ist ein Vektor der Länge 1. Eine Matrix ist im Prinzip auch ein Vektor, aber einer mit einem dim (dimension) Attribut:

# x ist ein Vektor
x <- 1:8

# Wir weisen nun x ein dim Attribut zu, d.h. wir machen aus
# x eine Matrix (hier mit 2 Zeilen und 4 Spalten)
dim(x) <- c(2, 4)
x
     [,1] [,2] [,3] [,4]
[1,]    1    3    5    7
[2,]    2    4    6    8
# Wir können Matrizen auch so erstellen:
m <- matrix(1:8, nrow = 2, ncol = 4, byrow = FALSE)
m
     [,1] [,2] [,3] [,4]
[1,]    1    3    5    7
[2,]    2    4    6    8
# Was sind die Dimensionen?
dim(m)
[1] 2 4

Beachten Sie das Argument byrow, welches den default Wert FALSE hat. Wenn wir das Argument byrow = TRUE setzen, dann erhalten wir:

m2 <- matrix(1:8, nrow = 2, ncol = 4, byrow = TRUE)
m2
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8

Dies führt dazu, dass die Zeilen zuerst aufgefüllt werden, während oben byrow = FALSE die Spalten zuerst aufgefüllt werden.

Wir können Matrizen transponieren, d.h. die Zeilen werden zu Spalten, und die Spalten werden zu Zeilen:

m_transponiert <- t(m)
m_transponiert
     [,1] [,2]
[1,]    1    2
[2,]    3    4
[3,]    5    6
[4,]    7    8

Es gibt zwei weitere Funktionen, welche wir kennenlernen sollten: cbind() und rbind(). Diese dienen dazu, Vektoren oder Matrizen zusammenzufügen.

cbind() kombiniert die Spalten (column-bind) von Vektoren/Matrizen zu einem Objekt:

x1 <- 1:3
# x1 ist ein Vektor
x1
[1] 1 2 3
x2 <- 10:12
# x2 ist ein Vektor
x2
[1] 10 11 12
m1 <- cbind(x1, x2)
# m1 ist eine Matrix mit den Dimensionen [3, 2]
m1
     x1 x2
[1,]  1 10
[2,]  2 11
[3,]  3 12

Daraus entsteht eine Matrix m1 mit den Ausgangsvektoren als Spalten.

rbind() kombiniert die Zeilen (row-bind) von Vektoren/Matrizen zu einem Objekt:

m2 <- rbind(x1, x2)
# m2 ist eine Matrix mit den Dimensionen [2, 3]
m2
   [,1] [,2] [,3]
x1    1    2    3
x2   10   11   12

Hier resultiert eine Matrix m2 mit den Ausgangsvektoren als Zeilen.

Auch Matrizen können mit [] indiziert werden. Wir müssen hier aber angeben, welche Zeile(n) und Spalte(n) wir erhalten wollen, und zwar mit [zeilennummer, spaltennummer].

Die Zeilennummer und Spaltennummer sind durch ein Komma getrennt. Wenn zeilennummer oder spaltennummer leer gelassen werden, heisst das: “Wähle alle Zeilen/Spalten aus.”

# Die erste Zellen: Zeile 1, Spalte 1
m1[1, 1]
x1 
 1 
# Zeile 1, Spalte 2
m1[1, 2]
x2 
10 
# Zeilen 2 bis 3, Spalte 1
m1[2:3, 1]
[1] 2 3
# Alle Zeilen, Spalte 1
m1[, 1]
[1] 1 2 3
# Zeile 2, alle Spalten
m1[2, ]
x1 x2 
 2 11

Vektorisierung

Alle Operatoren in R sind vektorisiert, d.h. sie operieren elementweise auf Vektoren:

x1 <- 1:10
x1 + 2
 [1]  3  4  5  6  7  8  9 10 11 12
x2 <- 11:20

x1 + x2
 [1] 12 14 16 18 20 22 24 26 28 30
x1 * x2
 [1]  11  24  39  56  75  96 119 144 171 200

Dasselbe gilt für Funktionen:

x1 <- 1:10

x1^2
 [1]   1   4   9  16  25  36  49  64  81 100
exp(x1)
 [1]     2.718282     7.389056    20.085537    54.598150   148.413159
 [6]   403.428793  1096.633158  2980.957987  8103.083928 22026.465795

Recycling

Etwas Besonderes in R ist das Vektor-Recycling: dies bedeutet, dass ein kürzerer Vektor wiederholt wird, wenn wir z.B. zwei Vektoren addieren. Dies kann oft nützlich sein, birgt aber auch Gefahren, wenn man sich dessen nicht bewusst ist.

# Der kürzere Vektor wird rezykliert:
1:10 + 1:2
 [1]  2  4  4  6  6  8  8 10 10 12

Was hier genau passiert, kann so dargestellt werden:

1  2  3  4  5  6  7  8  9 10
1  2  1  2  1  2  1  2  1  2

Der kürzere Vektor 1:2 wird so oft wie nötig wiederholt.

Was passiert, wenn der der längere Vektor nicht ein Vielfaches des kürzeren ist?

1:10 + 1:3
Warning in 1:10 + 1:3: longer object length is not a multiple of shorter object
length
 [1]  2  4  6  5  7  9  8 10 12 11

R führt zwar den Befehl aus, gibt uns aber auch eine Warnung.

1  2  3  4  5  6  7  8  9 10
1  2  3  1  2  3  1  2  3  1

Missing Values

Fehlende Werte werden mit NA deklariert. Wir werden diese im nächsten Kapitel kennenlernen.

zahlen <- c(12, 13, 15, 11, NA, 10)
zahlen
[1] 12 13 15 11 NA 10

Mit der Funktion is.na() kann man testen, ob etwas tatsächlich ein fehlender Wert ist:

is.na(zahlen)
[1] FALSE FALSE FALSE FALSE  TRUE FALSE
Hinweis

Fehlende Werte sind nicht zu verwechseln mit den Werten Inf (infinity) und NaN (not a number). Diese entstehen z.B. bei Division durch Null: 1/0 oder 0/0. Es gibt ausserdem noch den Datentyp NULL: diesen benutzen wir, wenn etwas undefiniert bleiben soll.

1/0
[1] Inf
0/0
[1] NaN

2.4.2 Character vectors

Character vectors werden benutzt, um Textelemente zu speichern und darzustellen. Die einzelnen Elemente eines Character-Vektors werden auch als “Strings” (Zeichenfolgen) bezeichnet. Dabei muss ein Element nicht aus einem einzelnen Wort bestehen, d.h. auch Leerzeichen können Teil eines Strings sein.

text <- c("these are", "some strings")
text
[1] "these are"    "some strings"
typeof(text)
[1] "character"
# text hat 2 Elemente:
length(text)
[1] 2

Wie numerische Vektoren können auch Character-Vektoren indiziert werden, d.h. wir können einzelne Elemente auswählen.

letters und LETTERS sind sogenannte built-in constants. Dies sind Vektoren mit allen Klein- bzw. Grossbuchstaben der englischen Sprache.

?letters
letters[1:3]
[1] "a" "b" "c"
letters[10:15]
[1] "j" "k" "l" "m" "n" "o"
LETTERS[24:26]
[1] "X" "Y" "Z"

Es gibt eine Funktion, mit der wir character vectors zusammenfügen können:

paste(LETTERS[1:3], letters[24:26], sep = "_")
[1] "A_x" "B_y" "C_z"
# Spezialfall mit sep = ""
paste0(1:3, letters[5:7])
[1] "1e" "2f" "3g"
vorname <- "Ronald Aylmer"
nachname <- "Fisher"
paste("Mein Name ist:", vorname, nachname, sep = " ")
[1] "Mein Name ist: Ronald Aylmer Fisher"
zahl <- 7
# zahl ist zwar eine ganze Zahl, wird aber durch paste() zu einem character
paste(zahl, "ist eine Zahl", sep = " ")
[1] "7 ist eine Zahl"

2.4.3 Logical vectors

Logische Vektoren können drei Werte annehmen: TRUE, FALSE oder NA.

log_var <- c(TRUE, FALSE, TRUE)
log_var
[1]  TRUE FALSE  TRUE

Logische Vektoren werden vor allem dazu benutzt, um numerische Vektoren zu indizieren, z.B. um alle positiven Elemente eines Vektors auszuwählen.

# x ist ein Vektor von standardnormalverteilten Zufallszahlen (d.h. wir ziehen 
# hier eine Zufallsstichprobe der Grösse n = 24 aus einer normalverteilten 
# Population mit dem Mittelwert 0 und der Standardabweichung 1). Die Funktion 
# `rnorm`, mit der wir die Zufallsstichprobe standardnormalverteilter Zahlen
# ziehen, werden wir zu einem späteren Zeitpunkt noch ausführlicher behandeln.
set.seed(5434) # macht das Beispiel reproduzierbar

x <- rnorm(24)
x
 [1]  1.06115528  0.87480990 -0.30032832  1.21965848  0.09860288  1.89862128
 [7] -1.54699798  0.96349219 -0.64968432 -1.09672125 -0.55326456 -0.29394388
[13]  0.58151046 -0.15135071  1.66997280 -0.10726874  0.51633289 -0.64741465
[19]  0.10489022 -0.95484078  0.22940461 -0.54106301 -0.76310004  1.22446844
# Wir brauchen nun einen logischen Vektor, der für jedes Element angibt, 
# ob dieses Element die Bedingung erfüllt (x soll positiv sein):
x > 0
 [1]  TRUE  TRUE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE
[13]  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE FALSE  TRUE
# Nun indizieren wir damit den Vektor x:
x[x > 0]
 [1] 1.06115528 0.87480990 1.21965848 0.09860288 1.89862128 0.96349219
 [7] 0.58151046 1.66997280 0.51633289 0.10489022 0.22940461 1.22446844
# Wir könnten den Index auch speichern 
index <- x > 0

# und damit x indizieren:
x[index]
 [1] 1.06115528 0.87480990 1.21965848 0.09860288 1.89862128 0.96349219
 [7] 0.58151046 1.66997280 0.51633289 0.10489022 0.22940461 1.22446844

Wir können auch alle Elemente von x suchen, welche eine Standardabweichung über dem Mittelwert liegen:

x
 [1]  1.06115528  0.87480990 -0.30032832  1.21965848  0.09860288  1.89862128
 [7] -1.54699798  0.96349219 -0.64968432 -1.09672125 -0.55326456 -0.29394388
[13]  0.58151046 -0.15135071  1.66997280 -0.10726874  0.51633289 -0.64741465
[19]  0.10489022 -0.95484078  0.22940461 -0.54106301 -0.76310004  1.22446844
x_mean <- mean(x)
x_sd <- sd(x)
x_mean
[1] 0.1182059
x_sd
[1] 0.9156615
x > (x_mean + x_sd)
 [1]  TRUE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
[13] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
x[x > (x_mean + x_sd)]
[1] 1.061155 1.219658 1.898621 1.669973 1.224468
# oder in einem Befehl
x[x > (mean(x) + sd(x))]
[1] 1.061155 1.219658 1.898621 1.669973 1.224468
Vertiefung

Wenn wir wissen wollen, welche Elemente des Vektors die Bedingung erfüllen, können wir die Funktion which() benützen.

# dies zeigt an, welche Elemente von x die Bedingung erfüllen
which(x > (mean(x) + sd(x)))
[1]  1  4  6 15 24

In diesem Beispiel liegen die Elemente 1, 4, 6, 15, 24 eine Standardabweichung oder mehr über dem Mittelwert. Wir können auch damit den Vektor indizieren; anstatt einen logischen Vektor zu verwenden, sagen wir einfach explizit, welche Elemente wir haben wollen.

x[which(x > (mean(x) + sd(x)))]
[1] 1.061155 1.219658 1.898621 1.669973 1.224468
# x[which(x > 0)] und x[x > 0] sind äquivalent
x[which(x > (mean(x) + sd(x)))] == x[x > (mean(x) + sd(x))]
[1] TRUE TRUE TRUE TRUE TRUE

2.4.4 Factors

Bisher haben wir numeric, logical und character Vektoren kennengelernt. Diese werden in R auch atomic vectors genannt, weil sie die fundamentalen Datentypen darstellen. Ein weiterer Objekttyp wird benötigt, um kategoriale Daten oder Gruppierungsvariablen darzustellen. Dieser Objekttyp wird factor genannt. Ein factor ist ein Vektor von natürlichen Zahlen (integer vector), der mit zusätzlicher Information (Metadaten) versehen ist. Diese attributes sind die Objektklasse factor und die Faktorstufen levels. Am besten wir illustrieren dies mit einem Beispiel.

# geschlecht ist ein character vector
geschlecht <- c("male", "female", "male", "nonbinary", "male", "female")
geschlecht
[1] "male"      "female"    "male"      "nonbinary" "male"      "female"   
typeof(geschlecht)
[1] "character"
attributes(geschlecht)
NULL

Nun können wir mit der Funktion factor() einen Faktor definieren:

geschlecht <- factor(geschlecht, levels = c("female", "male", "nonbinary"))
geschlecht
[1] male      female    male      nonbinary male      female   
Levels: female male nonbinary
# geschlecht hat nun den Datentyp integer
typeof(geschlecht)
[1] "integer"
# aber die `class` factor
class(geschlecht)
[1] "factor"
# und die Attribute levels und class
attributes(geschlecht)
$levels
[1] "female"    "male"      "nonbinary"

$class
[1] "factor"

Wir haben bei der Definition die levels explizit angegeben. Dies hätten wir nicht unbedingt tun müssen, da R automatisch die vorhandenen Strings in Faktorstufen konvertiert. Standardmässig werden die Faktorstufen alphabetisch geordnet, d.h. in der internen Definition der Faktorvariablen wird in diesem Fall female automatisch zur ersten Faktorstufe, male zur zweiten und nonbinary zur dritten Faktorstufe. Diese interne Definition der Faktorstufenreihenfolge ist unabhängig von der Reihenfolge des Auftretens bestimmter Ausprägungen/Faktorstufen in den Daten.

Vertiefung

Dass ein factor ein integer vector ist, erkennen wir, wenn wir das class Attribut entfernen, mit unclass(geschlecht). Dies wird auch im Environment-Bereich von RStudio angezeigt.

geschlecht
[1] male      female    male      nonbinary male      female   
Levels: female male nonbinary
unclass(geschlecht)
[1] 2 1 2 3 2 1
attr(,"levels")
[1] "female"    "male"      "nonbinary"

Faktoren werden wir später oft benötigen, wenn wir Regressionsmodelle mit Codiervariablen erstellen möchten. Die erste Stufe eines Faktors wird von R für solche Modelle automatisch als “Referenzkategorie” bestimmt. Manchmal wollen wir jedoch eine andere Faktorstufe als Referenzkategorie. In diesem Fall kann man die Reihenfolge der Faktorstufen ändern. Es gibt zwei Möglichkeiten: mit relevel() oder wie oben bereits gezeigt mit factor().

Mit relevel() kann die Referenzkategorie (und nur diese) direkt bestimmt werden. Die anderen Faktorstufen bleiben in ihrer ursprünglichen Reihenfolge.

levels(geschlecht)
[1] "female"    "male"      "nonbinary"
# Wir müssen das Resultat der Variable wieder zuweisen
geschlecht <- relevel(geschlecht, ref = "male")
levels(geschlecht)
[1] "male"      "female"    "nonbinary"
# Nur die Definition der Faktorstufenreihenfolge hat sich geändert hat, die 
# Daten selbst sind unverändert
geschlecht
[1] male      female    male      nonbinary male      female   
Levels: male female nonbinary

Mit factor() kann man die Reihenfolge genau bestimmen - es müssen aber alle Stufen explizit angegeben werden.

geschlecht
[1] male      female    male      nonbinary male      female   
Levels: male female nonbinary
geschlecht <- factor(geschlecht, levels = c("male", "nonbinary", "female"))
geschlecht
[1] male      female    male      nonbinary male      female   
Levels: male nonbinary female

Diese Änderungen der Faktorstufenreihenfolge erscheinen womöglich nicht sonderlich relevant, da sich ja an den Daten selbst nichts ändert, d.h. die Reihenfolge des Auftretens bestimmter Ausprägungen (Faktorstufen) in den Daten bleibt gleich, z.B. hat sich die vierte von sechs Personen als nonbinary bezeichnet, unabhängig davon, welche Faktorstufe als erste, zweite und dritte definiert ist. Wie oben schon gesagt, spielt die interne Definition der Faktorstufenreihenfolge später eine wichtige Rolle bei der Datenanalyse, daher ist es hilfreich, sich jetzt schon damit vertraut zu machen.

Vertiefung

Das levels-Attribut kann auch direkt angepasst werden, indem man diesem einen Vektor mit Faktorstufen zuweist. Aber Achtung, neben der Faktorstufenreihenfolge werden in diesem Fall auch die Daten angepasst!

# Kopie der Variablen erstellen, um später nicht durcheinander zu kommen
geschlecht_veraendert <- geschlecht

levels(geschlecht_veraendert) <- c("nonbinary", "male", "female")

# Vektor mit veränderter Faktorstufendefinition nochmal ausgeben
geschlecht_veraendert
[1] nonbinary female    nonbinary male      nonbinary female   
Levels: nonbinary male female

Personen, die vorher die erste Faktorstufe male aufwiesen, bekommen jetzt den Wert der neuen ersten Faktorstufe nonbinary zugewiesen; Personen, die vorher die zweite Faktorstufe nonbinary aufwiesen, bekommen jetzt den Wert der neuen zweiten Faktorstufe male zugewiesen; nur Personen mit Geschlecht female bekommen keinen anderen Wert zugewiesen, da es sich bei female um die neue und alte dritte Faktorstufe handelt.

Wegen des Verwirrungspotentials bei der Verwendung dieser Direktzuweisung von levels sollte diese Variante nur mit grösster Vorsicht verwendet werden (wir benötigen sie in diesem Kurs nicht).

Eine weitere nützliche Funktion für Faktoren ist table(). Damit können wir eine Häufigkeitstabelle erstellen. Wie oft kommt jede Faktorstufe in den Daten vor?

table(geschlecht)
geschlecht
     male nonbinary    female 
        3         1         2

2.4.5 Lists

Ein weiterer Datentyp ist list. Während Vektoren aus Elementen desselben Typs bestehen, können Listen aus heterogenen Elementen zusammengesetzt werden.

Listen werden mit der Funktion list() definiert:

x <- list(1:3, "a", c(TRUE, FALSE, TRUE), c(2.3, 5.9))
x
[[1]]
[1] 1 2 3

[[2]]
[1] "a"

[[3]]
[1]  TRUE FALSE  TRUE

[[4]]
[1] 2.3 5.9

Hier haben wir eine Liste x definiert, welche als Elemente einen numeric Vektor, einen character, einen logical Vektor und einen weiteren numeric Vektor enthält.

Listen können wie Vektoren indiziert werden:

x[1]
[[1]]
[1] 1 2 3
x[2]
[[1]]
[1] "a"
x[3]
[[1]]
[1]  TRUE FALSE  TRUE
x[4]
[[1]]
[1] 2.3 5.9
Vertiefung

Listen können auch mit [[ indiziert werden. Damit werden die Elemente noch weiter “entpackt”. Dies wird sehr gut in R for Data Science (Wickham, Çetinkaya-Rundel, et al., 2023) erklärt.

Wir werden in dieser Vorlesung selten selber Listen erstellen. Listen sind aber äusserst wichtig in R, und die statistischen Funktionen haben üblicherweise als Output eine Liste. Diese sind aber named lists, was bedeutet, dass die Elemente der Liste einen Namen haben. Erstellt wird eine named list so:

x <- list(int = 1:3,
          string = "a",
          log = c(TRUE, FALSE, TRUE),
          double = c(2.3, 5.9))
x
$int
[1] 1 2 3

$string
[1] "a"

$log
[1]  TRUE FALSE  TRUE

$double
[1] 2.3 5.9
# Der Typ einer Liste ist "list"
typeof(x)
[1] "list"

Die Elemente von x haben nun Namen, und können somit viel einfacher direkt ausgewählt werden. Dafür gibt es den speziellen $ Operator. Wenn Sie wissen, dass x eine Liste ist, Sie aber die Namen der Elemente nicht kennen, können Sie in der Konsole oder im Editor x$ schreiben, und dann TAB drücken. RStudio zeigt alle Elemente dieser Liste an.

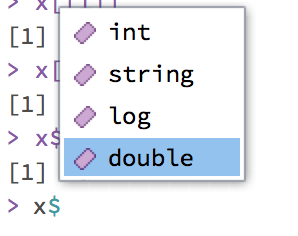
Diese Namen müssen nicht in Anführungszeichen geschrieben werden.

x$string
[1] "a"
x$double
[1] 2.3 5.9

2.4.6 Data Frames

Nun kommen wir zu dem für uns wichtigsten Objekt in R, dem Data Frame. Datensätze werden in R durch Data Frames repräsentiert. Ein Data Frame besteht aus Zeilen (rows) und Spalten (columns). Technisch gesehen ist ein Data Frame eine Liste, deren Elemente gleich lange (equal-length) Vektoren sind. Die Vektoren selber können numeric, logical oder character Vektoren sein, oder natürlich Faktoren. Numerische Variablen in einem Datensatz sollten demzufolge numeric Vektoren und kategoriale Variablen/Gruppierungsvariablen sollten factors sein. Ein Data Frame ist eine 2-dimensionale Struktur, und kann einerseits wie ein Vektor indiziert werden (genauer: wie eine Matrix), andererseits wie eine Liste.

Traditionell werden Data Frames in R mit der Funktion data.frame() definiert. In RStudio bzw. dem tidyverse-Package werden Data Frames neuerdings auch tibbles oder tbl genannt. tibbles werden mit der Funktion tibble() definiert, und stellen lediglich eine moderne Variante eines Data Frames dar. Sie erleichtern das Arbeiten mit Datensätzen.

Vertiefung

Genauer gesagt: wenn man tibble() beim Importieren von Datensätzen benützt, muss man weniger vorsichtig sein. RStudio macht das automatisch. Wir verwenden die Begriffe Data Frame und Tibble als Synonyme, auch wenn sie sich in einigen Merkmalen unterscheiden (Tibble hört sich an wie ‘table’, wenn man es mit einem neuseeländischen Akzent ausspricht).

Ein Data Frame wird so definiert:

library(dplyr)
df <- tibble(geschlecht = factor(c("male", "female",
                                   "male", "male",
                                   "female")),
             alter = c(22, 45, 33, 27, 30))
df
# A tibble: 5 × 2
  geschlecht alter
  <fct>      <dbl>
1 male          22
2 female        45
3 male          33
4 male          27
5 female        30

df ist nun ein Data Frame mit zwei Variablen, geschlecht und alter. Im Environment-Bereich von RStudio erscheinen Data Frames unter Data:

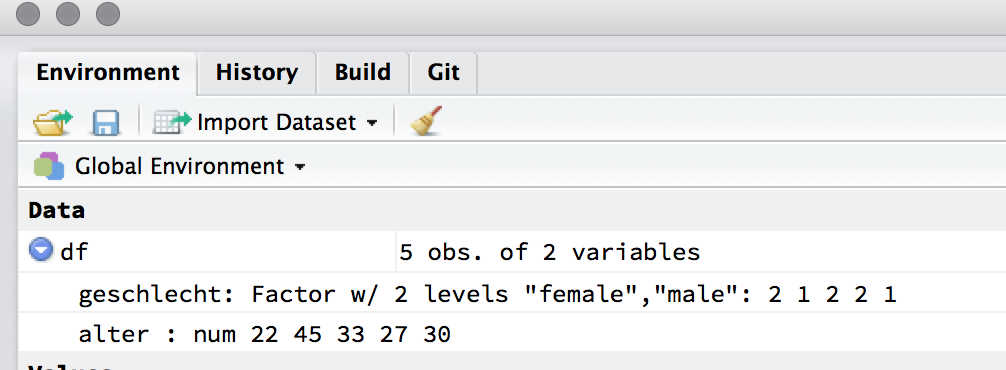
Ein Data Frame hat die Attribute names(), colnames() und rownames(), wobei names() und colnames() dasselbe bedeuten.

attributes(df)
$class
[1] "tbl_df"     "tbl"        "data.frame"

$row.names
[1] 1 2 3 4 5

$names
[1] "geschlecht" "alter"

Die Länge eines Data Frames ist die Länge der Liste, d.h. sie entspricht der Anzahl Spalten. Diese kann mit ncol() abgefragt werden, wogegen man mit nrow() die Anzahl Zeilen des Data Frames erhält.

ncol(df)
[1] 2
nrow(df)
[1] 5

Data Frame Subsetting

Wie oben erwähnt, kann ein Data Frame wie eine Liste indiziert werden, oder wie eine Matrix.

  • Wie eine Liste: die einzelnen Spalten können mit $ ausgewählt werden.
  • Wie eine Matrix: die Elemente können mit [ ausgewählt werden.
# Spaltennamen (Variablen) auswählen
df$geschlecht
[1] male   female male   male   female
Levels: female male
df$alter
[1] 22 45 33 27 30
df["geschlecht"]
# A tibble: 5 × 1
  geschlecht
  <fct>     
1 male      
2 female    
3 male      
4 male      
5 female    
df["alter"]
# A tibble: 5 × 1
  alter
  <dbl>
1    22
2    45
3    33
4    27
5    30
# Nach Position auswählen
df[1]
# A tibble: 5 × 1
  geschlecht
  <fct>     
1 male      
2 female    
3 male      
4 male      
5 female    
df[2]
# A tibble: 5 × 1
  alter
  <dbl>
1    22
2    45
3    33
4    27
5    30

Ähnlich wie bei Matrizen können Zeilen und Spalten ausgewählt werden, auch hier mit [zeilennummer, spaltennummer].

# Erste Zeile, erste Spalte
df[1, 1]
# A tibble: 1 × 1
  geschlecht
  <fct>     
1 male      
# Erste Zeile, alle Spalten
df[1, ]
# A tibble: 1 × 2
  geschlecht alter
  <fct>      <dbl>
1 male          22
# ALle Zeilen, erste Spalte
df[, 1]
# A tibble: 5 × 1
  geschlecht
  <fct>     
1 male      
2 female    
3 male      
4 male      
5 female    
# Alle Zeilen, alle Spalten
df[ , ]
# A tibble: 5 × 2
  geschlecht alter
  <fct>      <dbl>
1 male          22
2 female        45
3 male          33
4 male          27
5 female        30
# Wir können auch Sequenzen verwenden
# Die ersten drei Zeilen, alle Spalten
df[1:3, ]
# A tibble: 3 × 2
  geschlecht alter
  <fct>      <dbl>
1 male          22
2 female        45
3 male          33

Da die Spalten Vektoren sind, können wir diese auch indizieren:

df$geschlecht[1]
[1] male
Levels: female male
# oder

df$alter[2:3]
[1] 45 33

2.5 Übungsaufgaben

Zahlen runden

x <- rnorm(10, mean = 1, sd = 0.5)
x
 [1]  0.66851021  1.60952322  0.62064523  0.62563620  1.31433575  1.10078969
 [7]  0.48313164 -0.02969281  0.71076782  0.85972382
  1. Runden Sie den Vektor x auf 0 Dezimalstellen.
round(x = x, digits = 0)
 [1] 1 2 1 1 1 1 0 0 1 1
  1. Runden Sie den Vektor x auf 3 Dezimalstellen.
round(x, digits = 3)
 [1]  0.669  1.610  0.621  0.626  1.314  1.101  0.483 -0.030  0.711  0.860
  1. Runden Sie zahl auf die nächste natürliche Zahl auf/ab.
(zahl <- 3.45263)
[1] 3.45263
ceiling(zahl)
[1] 4
floor(zahl)
[1] 3

Mittelwert berechnen

  1. Berechnen Sie den Mittelwert der Variable alter in folgendem Data Frame:
df <- tibble(geschlecht = sample(c("male", "female"),
                                 size = 24,
                                 replace = TRUE),
             alter = runif(24, min = 19, max = 45))
df
# A tibble: 24 × 2
   geschlecht alter
   <chr>      <dbl>
 1 male        22.1
 2 female      22.6
 3 male        24.4
 4 female      40.7
 5 female      22.0
 6 female      42.1
 7 female      22.1
 8 female      41.7
 9 male        38.2
10 male        44.1
# ℹ 14 more rows
mean(df$alter)
[1] 31.17342
  1. Lassen Sie sich deskriptive Statistiken ausgeben (summary()).
summary(df)
  geschlecht            alter      
 Length:24          Min.   :20.27  
 Class :character   1st Qu.:24.29  
 Mode  :character   Median :30.15  
                    Mean   :31.17  
                    3rd Qu.:37.94  
                    Max.   :44.08

Matrizen

  1. Kombinieren Sie die beiden Matrizen m1 und m2 (beide mit den Dimensionen [12, 4]), so dass eine neue Matrix m3 entsteht, mit den Dimensionen [24, 4].
m1 <- matrix(rnorm(48, mean = 110, sd = 5), ncol = 4)
m2 <- matrix(rnorm(48, mean = 100, sd = 10), ncol = 4)
m1
          [,1]     [,2]     [,3]     [,4]
 [1,] 112.6577 110.3748 114.1209 104.0900
 [2,] 116.7024 120.9622 111.6725 113.6405
 [3,] 114.4603 109.6374 107.9318 102.1479
 [4,] 109.8077 109.1152 108.8644 114.3867
 [5,] 113.5108 110.4932 100.2663 112.1465
 [6,] 119.0698 110.9733 113.7455 111.6653
 [7,] 109.4984 114.9592 106.6855 106.4838
 [8,] 110.6606 112.5256 111.0061 114.9715
 [9,] 108.3435 101.4709 107.8447 107.2151
[10,] 108.1350 110.0513 112.4929 101.0572
[11,] 110.8037 113.1775 113.9552 102.4492
[12,] 104.0074 103.4657 110.5090 110.2850
m2
           [,1]      [,2]      [,3]      [,4]
 [1,] 107.06283  97.57565 100.09972 106.05653
 [2,]  94.31888 121.33598  89.61459 120.11837
 [3,]  94.44192 102.61623 113.93752  89.38039
 [4,]  82.87758 108.59534 101.22006  94.78172
 [5,]  97.84665 114.72505 104.53691  97.47717
 [6,] 108.32954  89.14035 107.05284  88.84799
 [7,] 112.39876 120.85322  93.22207 116.04059
 [8,] 111.42864  98.94615 113.08818  99.33227
 [9,] 111.44163  99.61579 102.23889  94.39533
[10,] 110.92366  92.24573  89.61547 115.96388
[11,]  95.51570 114.81185  91.85183 102.81788
[12,] 113.37321  88.37608 109.54577 100.70044
m3 <- rbind(m1, m2)
m3
           [,1]      [,2]      [,3]      [,4]
 [1,] 112.65772 110.37480 114.12094 104.09003
 [2,] 116.70244 120.96217 111.67248 113.64050
 [3,] 114.46026 109.63743 107.93183 102.14786
 [4,] 109.80768 109.11518 108.86436 114.38675
 [5,] 113.51080 110.49324 100.26626 112.14648
 [6,] 119.06984 110.97326 113.74550 111.66534
 [7,] 109.49837 114.95920 106.68548 106.48376
 [8,] 110.66056 112.52559 111.00613 114.97145
 [9,] 108.34351 101.47088 107.84474 107.21505
[10,] 108.13497 110.05134 112.49292 101.05717
[11,] 110.80370 113.17754 113.95516 102.44920
[12,] 104.00743 103.46569 110.50899 110.28505
[13,] 107.06283  97.57565 100.09972 106.05653
[14,]  94.31888 121.33598  89.61459 120.11837
[15,]  94.44192 102.61623 113.93752  89.38039
[16,]  82.87758 108.59534 101.22006  94.78172
[17,]  97.84665 114.72505 104.53691  97.47717
[18,] 108.32954  89.14035 107.05284  88.84799
[19,] 112.39876 120.85322  93.22207 116.04059
[20,] 111.42864  98.94615 113.08818  99.33227
[21,] 111.44163  99.61579 102.23889  94.39533
[22,] 110.92366  92.24573  89.61547 115.96388
[23,]  95.51570 114.81185  91.85183 102.81788
[24,] 113.37321  88.37608 109.54577 100.70044
  1. Wählen Sie aus m3 die Elemente so aus (mit Matrix subsetting), dass Sie die ursprüngliche Matrix m1 erhalten.
m3[1:12,]
          [,1]     [,2]     [,3]     [,4]
 [1,] 112.6577 110.3748 114.1209 104.0900
 [2,] 116.7024 120.9622 111.6725 113.6405
 [3,] 114.4603 109.6374 107.9318 102.1479
 [4,] 109.8077 109.1152 108.8644 114.3867
 [5,] 113.5108 110.4932 100.2663 112.1465
 [6,] 119.0698 110.9733 113.7455 111.6653
 [7,] 109.4984 114.9592 106.6855 106.4838
 [8,] 110.6606 112.5256 111.0061 114.9715
 [9,] 108.3435 101.4709 107.8447 107.2151
[10,] 108.1350 110.0513 112.4929 101.0572
[11,] 110.8037 113.1775 113.9552 102.4492
[12,] 104.0074 103.4657 110.5090 110.2850
m1
          [,1]     [,2]     [,3]     [,4]
 [1,] 112.6577 110.3748 114.1209 104.0900
 [2,] 116.7024 120.9622 111.6725 113.6405
 [3,] 114.4603 109.6374 107.9318 102.1479
 [4,] 109.8077 109.1152 108.8644 114.3867
 [5,] 113.5108 110.4932 100.2663 112.1465
 [6,] 119.0698 110.9733 113.7455 111.6653
 [7,] 109.4984 114.9592 106.6855 106.4838
 [8,] 110.6606 112.5256 111.0061 114.9715
 [9,] 108.3435 101.4709 107.8447 107.2151
[10,] 108.1350 110.0513 112.4929 101.0572
[11,] 110.8037 113.1775 113.9552 102.4492
[12,] 104.0074 103.4657 110.5090 110.2850
m3[1:12,] == m1
      [,1] [,2] [,3] [,4]
 [1,] TRUE TRUE TRUE TRUE
 [2,] TRUE TRUE TRUE TRUE
 [3,] TRUE TRUE TRUE TRUE
 [4,] TRUE TRUE TRUE TRUE
 [5,] TRUE TRUE TRUE TRUE
 [6,] TRUE TRUE TRUE TRUE
 [7,] TRUE TRUE TRUE TRUE
 [8,] TRUE TRUE TRUE TRUE
 [9,] TRUE TRUE TRUE TRUE
[10,] TRUE TRUE TRUE TRUE
[11,] TRUE TRUE TRUE TRUE
[12,] TRUE TRUE TRUE TRUE

Character vectors

Generieren Sie aus den Variablen ID, Initialen und Alter eine neue Variable, welche so aussieht:

"1-RS-44" "2-MM-78" "3-PD-22" "4-PG-34" "5-DK-67" "1-RS-59"
ID <- c(1, 2, 3, 4, 5)
Initialen <- c("RS", "MM", "PD", "PG", "DK")
Alter <- c(44, 78, 22, 34, 67, 59)
personen <- paste(ID, Initialen, Alter, sep = "-")
personen
[1] "1-RS-44" "2-MM-78" "3-PD-22" "4-PG-34" "5-DK-67" "1-RS-59"

Data Frame

Ändern Sie die Reihenfolge der Faktorstufen des Datensatzes alk_aggr, so dass placebo die Referenzkategorie bildet.

library(dplyr)
library(tidyr)

kein_alkohol <- c(64, 58, 64)
placebo <- c(74, 79, 72)
anti_placebo <- c(71, 69, 67)
alkohol <- c(69, 73, 74)

alk_aggr <- tibble(kein_alkohol = kein_alkohol,
                   placebo = placebo,
                   anti_placebo = anti_placebo,
                   alkohol = alkohol)

alk_aggr <- alk_aggr |>
  pivot_longer(everything(), 
               names_to = "alkoholbedingung", 
               values_to = "aggressivitaet") |>
  mutate(alkoholbedingung = factor(alkoholbedingung))

alk_aggr
# A tibble: 12 × 2
   alkoholbedingung aggressivitaet
   <fct>                     <dbl>
 1 kein_alkohol                 64
 2 placebo                      74
 3 anti_placebo                 71
 4 alkohol                      69
 5 kein_alkohol                 58
 6 placebo                      79
 7 anti_placebo                 69
 8 alkohol                      73
 9 kein_alkohol                 64
10 placebo                      72
11 anti_placebo                 67
12 alkohol                      74
levels(alk_aggr$alkoholbedingung)
[1] "alkohol"      "anti_placebo" "kein_alkohol" "placebo"     
alk_aggr$alkoholbedingung <- factor(alk_aggr$alkoholbedingung, 
                                    levels = c("placebo", 
                                               "anti_placebo", 
                                               "kein_alkohol", 
                                               "alkohol"))
levels(alk_aggr$alkoholbedingung)
[1] "placebo"      "anti_placebo" "kein_alkohol" "alkohol"     
# alternative Lösung
alk_aggr$alkoholbedingung <- relevel(alk_aggr$alkoholbedingung, ref = "placebo")
levels(alk_aggr$alkoholbedingung)
[1] "placebo"      "anti_placebo" "kein_alkohol" "alkohol"

Fortgeschrittene Aufgabe

  1. Wählen Sie aus einem numerischen Vektor nur die geraden Zahlen:
x <- seq(1, 20, by = 1)
x
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Tipp: Sie brauchen dafür den modulo operator %%. Geraden Zahlen sind durch 2 teilbar, d.h. es gibt bei der ganzzahligen Teilung keinen Rest.

# Gerade Zahlen sind durch 2 teilbar. Wir wollen nun für jedes Element in `x` den Rest, wenn wir durch 2 teilen:    
x %% 2
 [1] 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0
# Dies gibt uns einen logischen Vektor; wir machen daraus eine Indexvariable:
index <- x %% 2 == 0
index
 [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE
[13] FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE  TRUE
# Und nun müssen wir damit `x` indizieren:
gerade_zahlen <- x[index]
gerade_zahlen
 [1]  2  4  6  8 10 12 14 16 18 20
  1. Machen Sie dasselbe für ungerade Zahlen.
x <- seq(1, 20, by = 1)
x
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
# wir wählen alle Zahlen aus, deren Rest ungleich Null ist
index <- x %% 2 != 0

# und indizieren damit x
ungerade_zahlen <- x[index]

ungerade_zahlen
 [1]  1  3  5  7  9 11 13 15 17 19
# dasselbe in einer Zeile:
x[x %% 2 != 0]
 [1]  1  3  5  7  9 11 13 15 17 19