library(tidyverse)
library(haven)
beispieldaten <- read_sav("data/beispieldaten.sav") |>
# Faktoren konvertieren und SPSS-Labels zuweisen
mutate(across(where(is.labelled), haven::as_factor)) |>
# Labels der Bildungsfaktoren vereinfachen
mutate(across(c(bildung_vater, bildung_mutter),
\(x) fct_recode(x,
Hauptschule = "Hauptschulabschluss oder niedriger",
Realschule = "Realschulabschluss (mittlere Reife)",
Abitur = "Fachabitur, Abitur",
Hochschule = "Fachhochschulabschluss, Universitätsabschluss")))5 Grafiken mit ggplot2
Grafiken sind für die Datenanalyse sehr wichtig. Einerseits können wir sie für explorative Datenanalyse einsetzen, um eventuell verborgene Zusammenhänge zu entdecken oder uns einfach einen Überblick zu verschaffen. Andererseits brauchen wir Grafiken, um Resultate darzustellen und anderen zu kommunizieren.
Wir haben schon mehrmals in diesem Skript Grafiken mit dem Package ggplot2 erstellt, ohne uns den Code genauer anzuschauen. In diesem Kapitel werden wir nun die Syntax von ggplot2 kennenlernen.
Im Gegensatz dazu basiert ggplot2 auf einer intuitiven Syntax, der sogenannten Grammar of graphics. Sobald man sich daran gewöhnt hat, kann man mit einer eleganten und konsistenten “Grammatik” sehr komplexe Grafiken erstellen. ggplot2 ist darauf ausgelegt, mit tidy Data zu arbeiten, d.h. wir brauchen Datensätze im long Format. Grafiken werden nun immer nach demselben Prinzip erstellt:
Schritt 1: Wir beginnen mit einem Datensatz und erstellen ein Plot-Objekt mit der Funktion ggplot().
Schritt 2: Wir definieren sogenannte “aesthetic mappings”, d.h. wir bestimmen welche Variablen auf den X-, bzw. Y-Achsen dargestellt werden sollen, und welche Variablen benutzt werden, um die Daten zu gruppieren. Die Funktion, welche wir dafür benutzen heisst aes().
Schritt 3: Wir fügen dem Plot eine oder mehrere “Layers” oder “Schichten” hinzu. Diese Layers definieren, wie etwas dargestellt werden soll, z.B. als Linie oder als Histogramm. Die Funktionen beginnen mit dem Präfix geom_, z.B. geom_line().
Um ggplot2 zu benutzen brauchen wir nun noch einen zusätzlichen Operator: +. Diesen kennen Sie bereits als mathematischen Operator, aber in diesem Zusammenhang bedeutet die Verwendung von +, dass wir einzelne Elemente eines Plot-Objektes zusammenfügen.
Nach dieser etwas abstrakten Einführung illustrieren wir diese Schritte an einem praktischen Beispiel.
Am Ende des letzten Kapitels haben wir den Zusammenhang zwischen psychischem Stress und Geschlecht untersucht. Wir laden nun nochmals den Datensatz:
und erstellen einen Datensatz, der nur die Variablen ID, geschlecht und stress_psychisch enthält.
stress <- beispieldaten |>
select(ID, geschlecht, stress_psychisch) |>
drop_na()
stress# A tibble: 284 × 3
ID geschlecht stress_psychisch
<dbl> <fct> <dbl>
1 1 weiblich 1.67
2 2 männlich 3.5
3 10 weiblich 3.67
4 11 weiblich 1.5
5 12 weiblich 2.5
6 14 männlich 1
7 15 männlich 2.5
8 16 weiblich 3.5
9 17 männlich 1.67
10 18 männlich 2.5
# ℹ 274 more rowsIn diesem Datensatz haben wir eine numerische Variable, stress_psychisch und eine Gruppierungsvariable, geschlecht. Wir wollen die Verteilung von stress_psychisch zwischen männlichen und weiblichen Jugendlichen vergleichen. Die Verteilung können wir auf verschiedene Arten grafisch darstellen: mit Punkten, einem Boxplot oder einem Violin-Plot. Diese drei Methoden sind in der Sprache von ggplot2 verschiedene geoms und können so benutzt werden: geom_point(), geom_boxplot() oder geom_violin(). Zusätzlich gibt es noch eine Funktion geom_jitter(), welche die Punkte in einem Punktdiagramm nicht aufeinander zeichnet, sondern mit einem zufälligen horizontalen “jittering” (Flackern) versieht.
Das ggplot2 Package können wir entweder individuell oder als Teil des tidyverse laden:
library(ggplot2)
# oder
library(tidyverse)5.1 Schritt 1: Plot-Objekt erstellen
Wir beginnen mit einem Datensatz und erstellen ein Plot-Objekt mit der Funktion ggplot(). Diese Funktion hat als erstes Argument einen Dataframe. Dies bedeutet, dass wir den pipe Operator verwenden können:
Wir haben also zwei Möglichkeiten. Wir bevorzugen hier die pipe Notation, aber es ist selbstverständlich auch möglich, den Dataframe innerhalb der Funktion als Argument anzugeben. Gleichzeitig weisen wir das Objekt einer Variablen zu, und nennen diese p.
# 1. Variante
p <- ggplot(data = stress)
# 2. Variante
p <- stress |>
ggplot()5.2 Schritt 2: Aesthetic mappings
Nun definieren wir mit dem zweiten Argument mapping die aesthetic mappings. Diese bestimmen, wie die Variablen benutzt werden, um die Daten darzustellen, und werden mit der Funktion aes() definiert. Wir wollen die Gruppierungsvariable geschlecht auf der X-Achse darstellen und stress_psychisch soll auf der Y-Achse angezeigt werden. Zusätzlich kann aes() weitere Argumente haben: fill, color, shape, linetype, group. Diese werden dazu benutzt, um den Stufen der Gruppierungsvariablen (Faktoren) unterschiedliche Farben, Formen, Linien, etc. zuzuweisen.
In diesem Beispiel haben wir die Gruppierungsvariable geschlecht und wir wollen, dass die beiden Stufen von geschlecht verschiedene Farben haben und mit verschiedenen Farben “ausgefüllt” werden.
Wenn wir die aesthetic mappings innerhalb der Funktion ggplot() definieren, gelten sie für alle Layers, d.h. für alle Elemente des Plots. Wir könnten diese mappings auch für jede Layer separat definieren.
p <- stress |>
ggplot(mapping = aes(
x = geschlecht,
y = stress_psychisch,
color = geschlecht,
fill = geschlecht
))p ist nun ein “leeres” Plot-Objekt. Wir können es uns anschauen, aber es wird noch nichts angezeigt, da es noch keine Layers enthält:
p
# oder print(p)Wir sehen, dass ggplot2 für uns schon die Achsen anhand der Variablennamen beschriftet hat.
5.3 Schritt 3: geoms hinzufügen
Dem Plot-Objekt p können wir nun mit geom_ Funktionen Layers hinzufügen. Die Syntax funktioniert so: Wir “addieren” zu dem Plot-Objekt p ein geom: p + geom_
5.3.1 Punktdiagramm
Wir versuchen zuerst, die Beobachtungen als Punkte darzustellen:
# die Funktion geom_point() hat ein size Argument
p + geom_point(size = 3)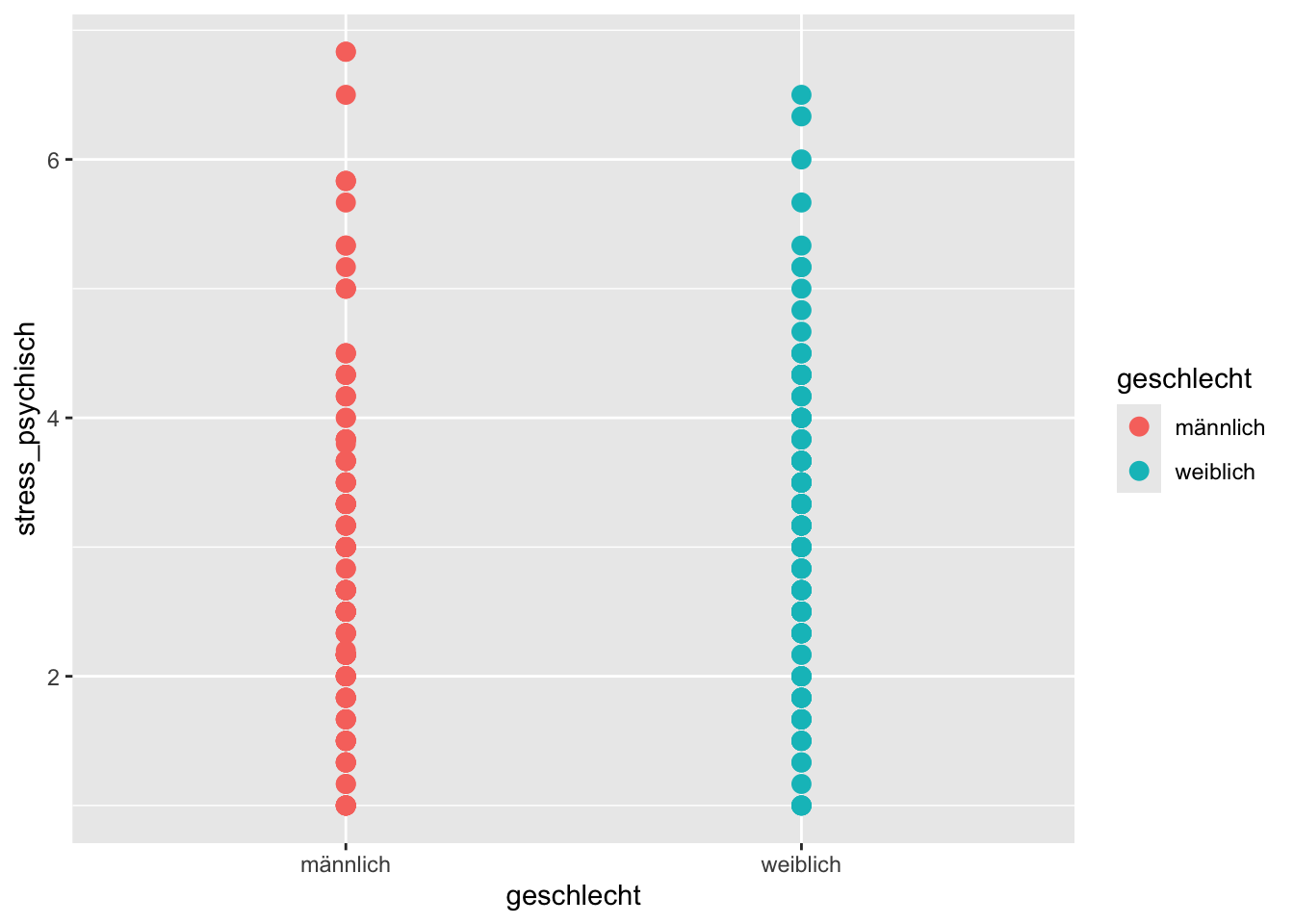
Die Punkte werden nun in verschiedenen Farben dargestellt, aber innerhalb eines Geschlechts werden Punkte eventuell übereinander geplottet, wenn sie denselben Wert haben (overplotting). Für diesen Fall gibt es die Funktion geom_jitter(), welche Punkte mit einem jittering nebeneinander zeichnet:
p + geom_jitter()
geom_jitter() hat ein Argument width, mit dem wir bestimmen können, wie breit die Streuung der Punkte ist.
p + geom_jitter(width = 0.2)
geom_jitter() hat weitere Argumente: size bestimmt den Durchmesser der Punkte, und alpha bestimmt die Transparenz.
p + geom_jitter(width = 0.2, size = 4, alpha = 0.6)
5.3.2 Verteilung grafisch darstellen
Eine weitere Möglichkeit wäre, die zentrale Tendenz und Streuung der Daten mit einem Boxplot- oder Violin-Diagramm darzustellen.
p + geom_boxplot()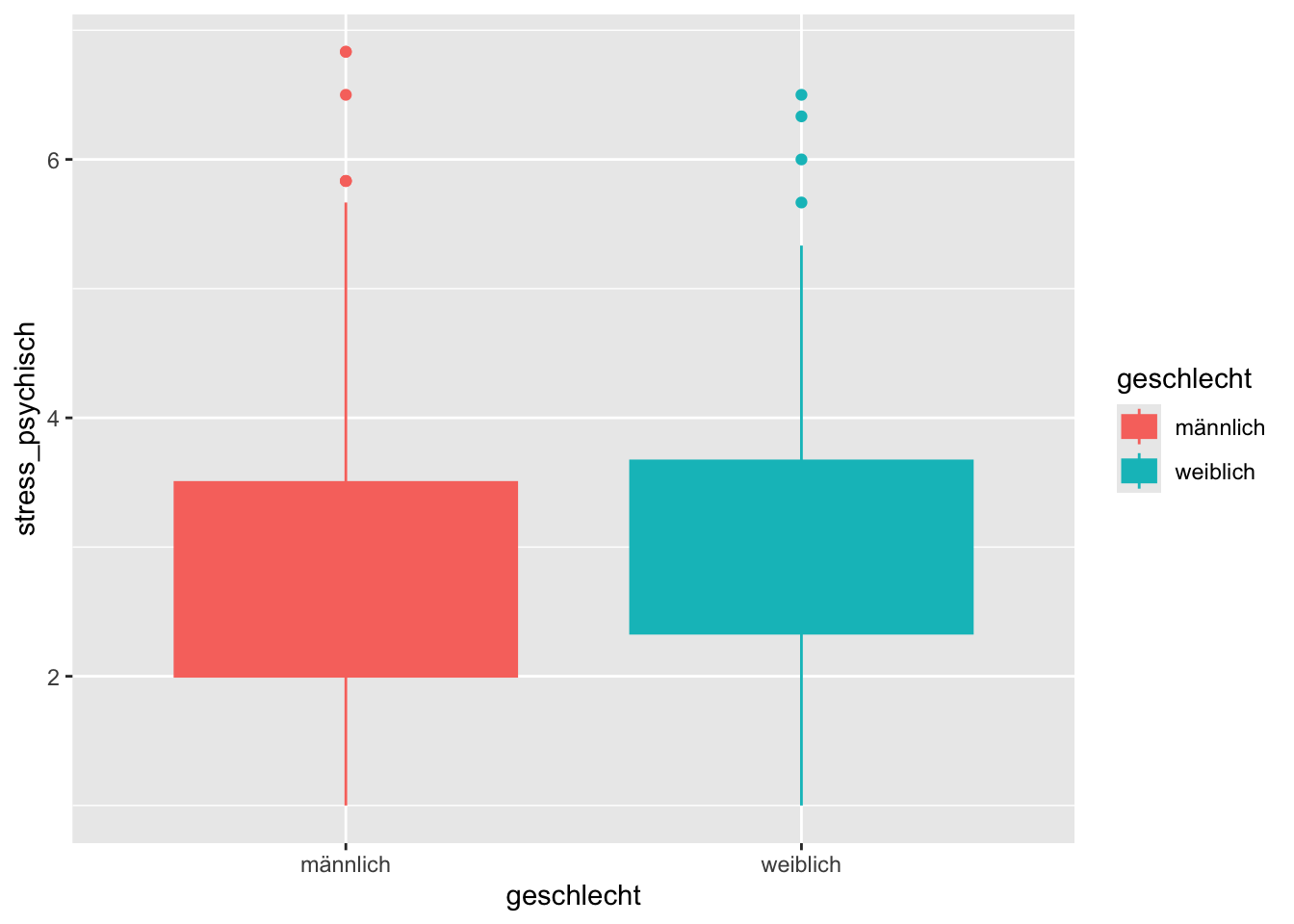
In einem Boxplot wird der Median dargestellt, das Rechteck repräsentiert die mittleren 50%, und die “whiskers” zeigen 1.5 * den Interquartilsbereich. Ausreisser werden mit Punkten dargestellt. Um den Median zu sehen, ist es besser, wenn wir das fill Attribut weglassen:
p <- stress |>
ggplot(mapping = aes(
x = geschlecht,
y = stress_psychisch,
color = geschlecht
))
p + geom_boxplot()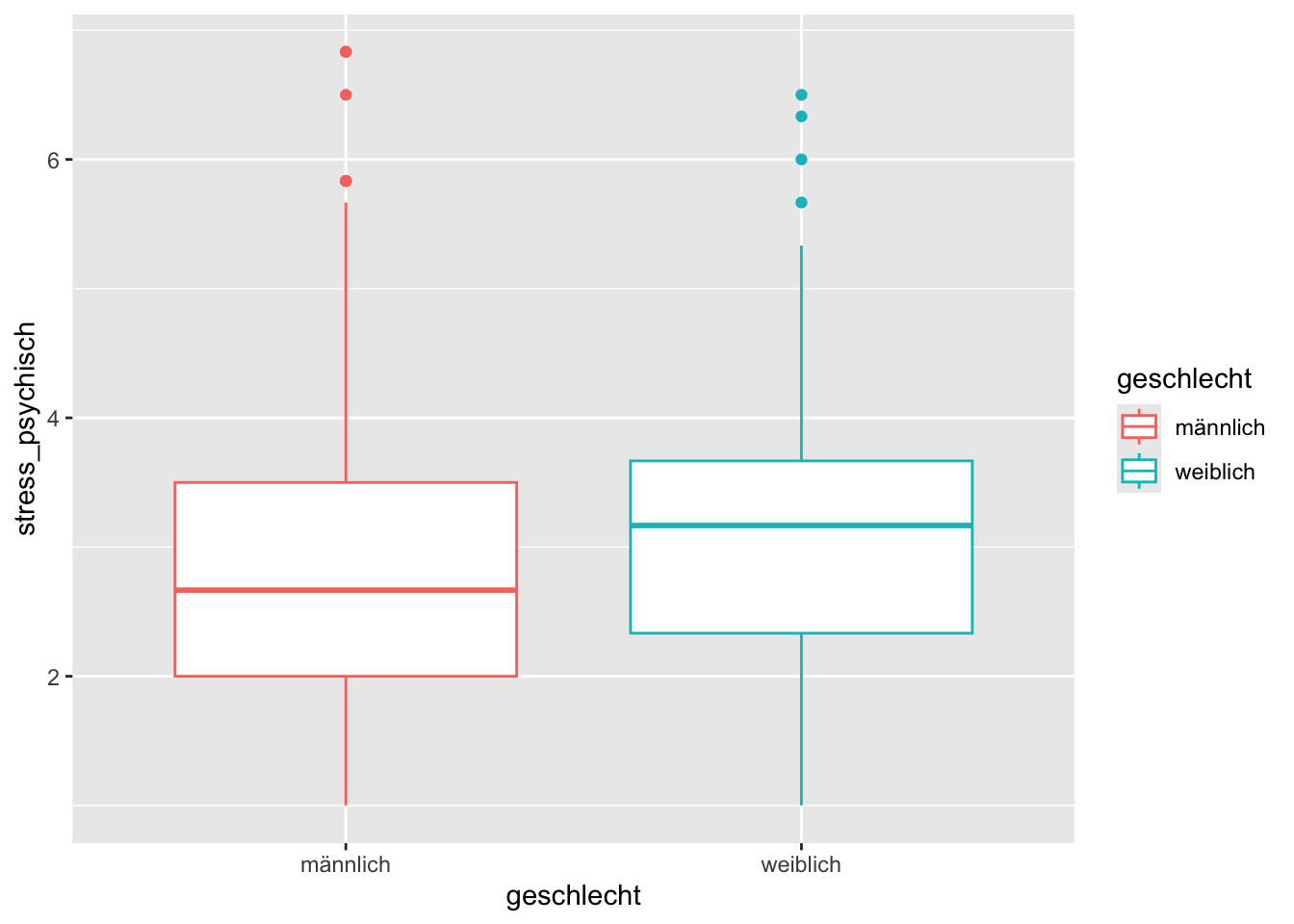
Ein Violin-Plot ist ähnlich wie ein Boxplot, zeigt aber nicht die Quantile, sondern ein “kernel density estimate”. Ein Violin-Plot sieht am besten aus, wenn wir das fill Attribut verwenden.
p <- stress |>
ggplot(mapping = aes(
x = geschlecht,
y = stress_psychisch,
fill = geschlecht
))
p + geom_violin()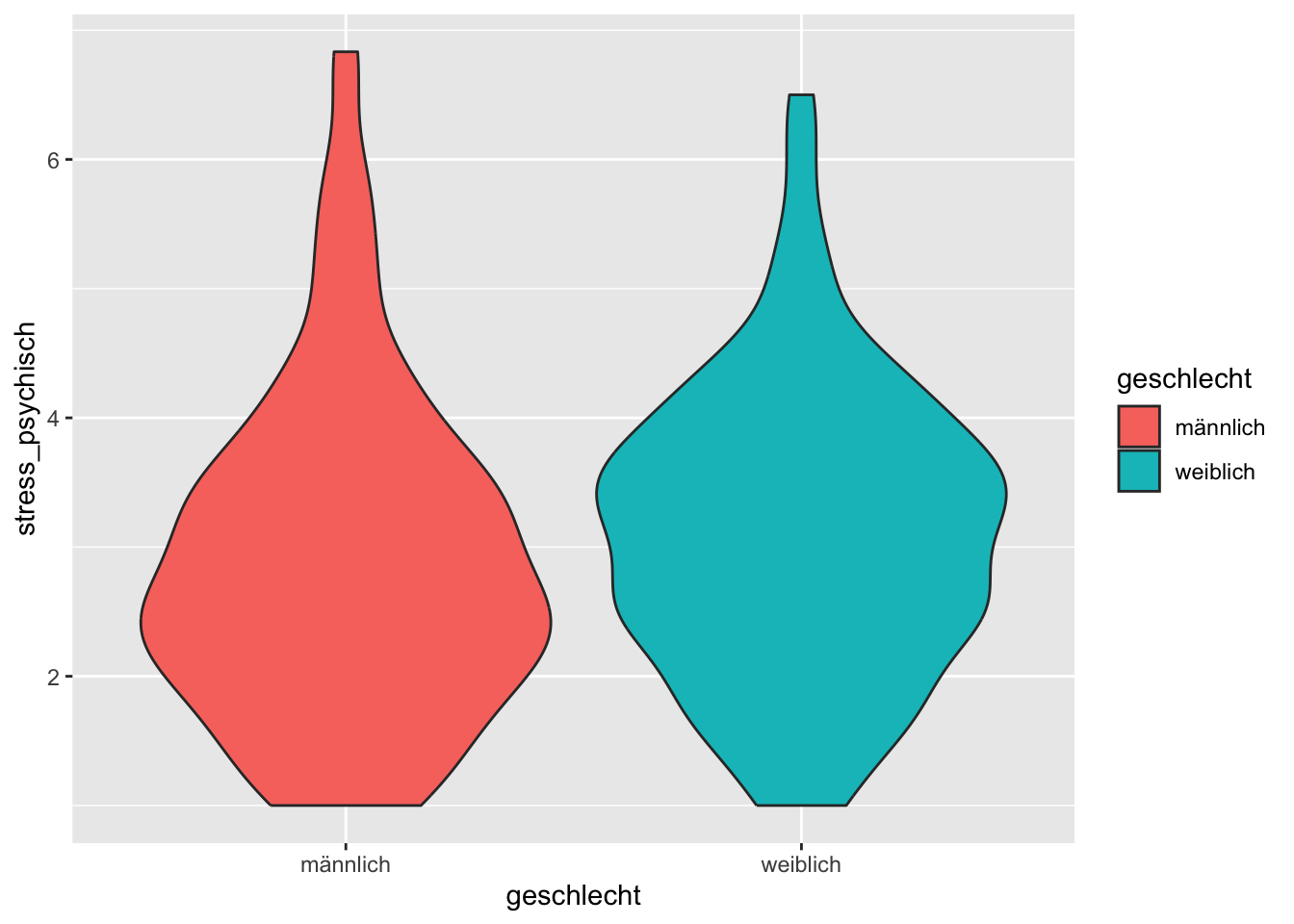
Wenn wir feststellen, dass ein Mapping nicht für alle “Layers” gelten soll, dann können wir es für jede Layer individuell definieren, anstatt in der ggplot() Funktion:
p <- stress |>
ggplot(mapping = aes(
x = geschlecht,
y = stress_psychisch
))p + geom_boxplot(mapping = aes(color = geschlecht))# oder einfach
p + geom_boxplot(aes(color = geschlecht))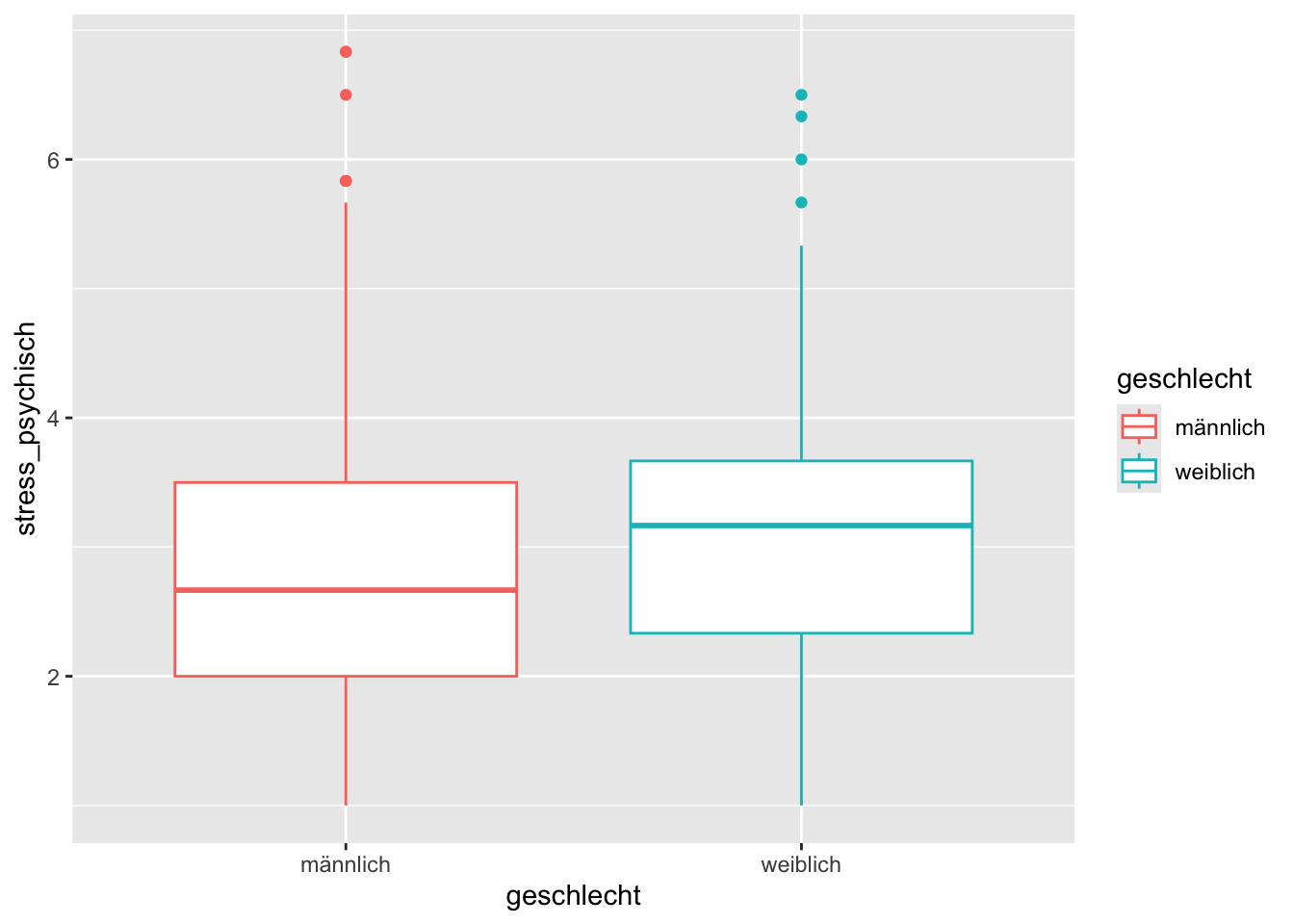
p + geom_violin(aes(fill = geschlecht))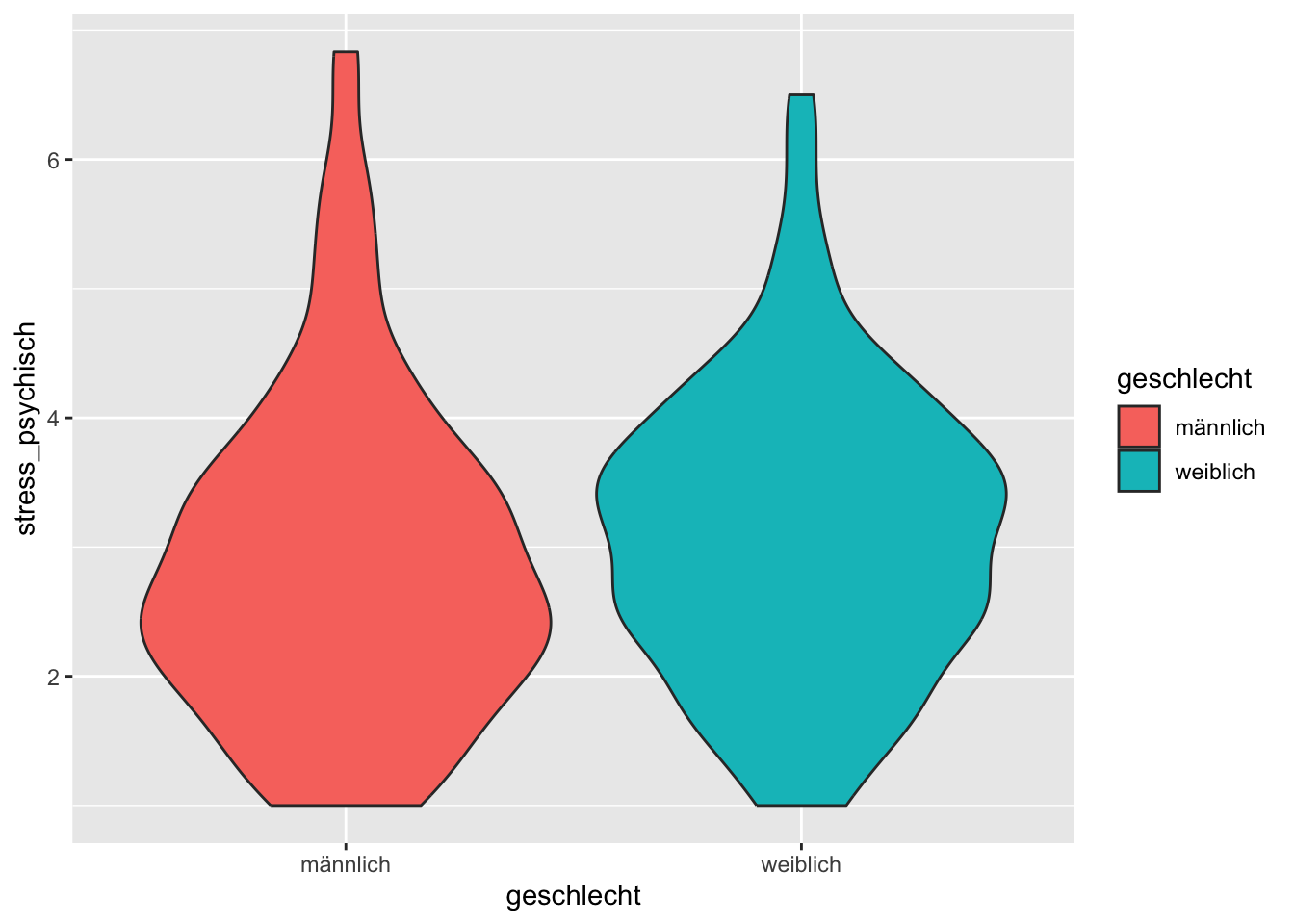
5.3.3 Mehrere Layers kombinieren
Wir können auch mehrere Layers verwenden. Wir müssen lediglich mehrere geom_ Funktionen mit einem + zusammenfügen:
p +
geom_violin(aes(fill = geschlecht)) +
geom_jitter(width = 0.2, alpha = 0.6)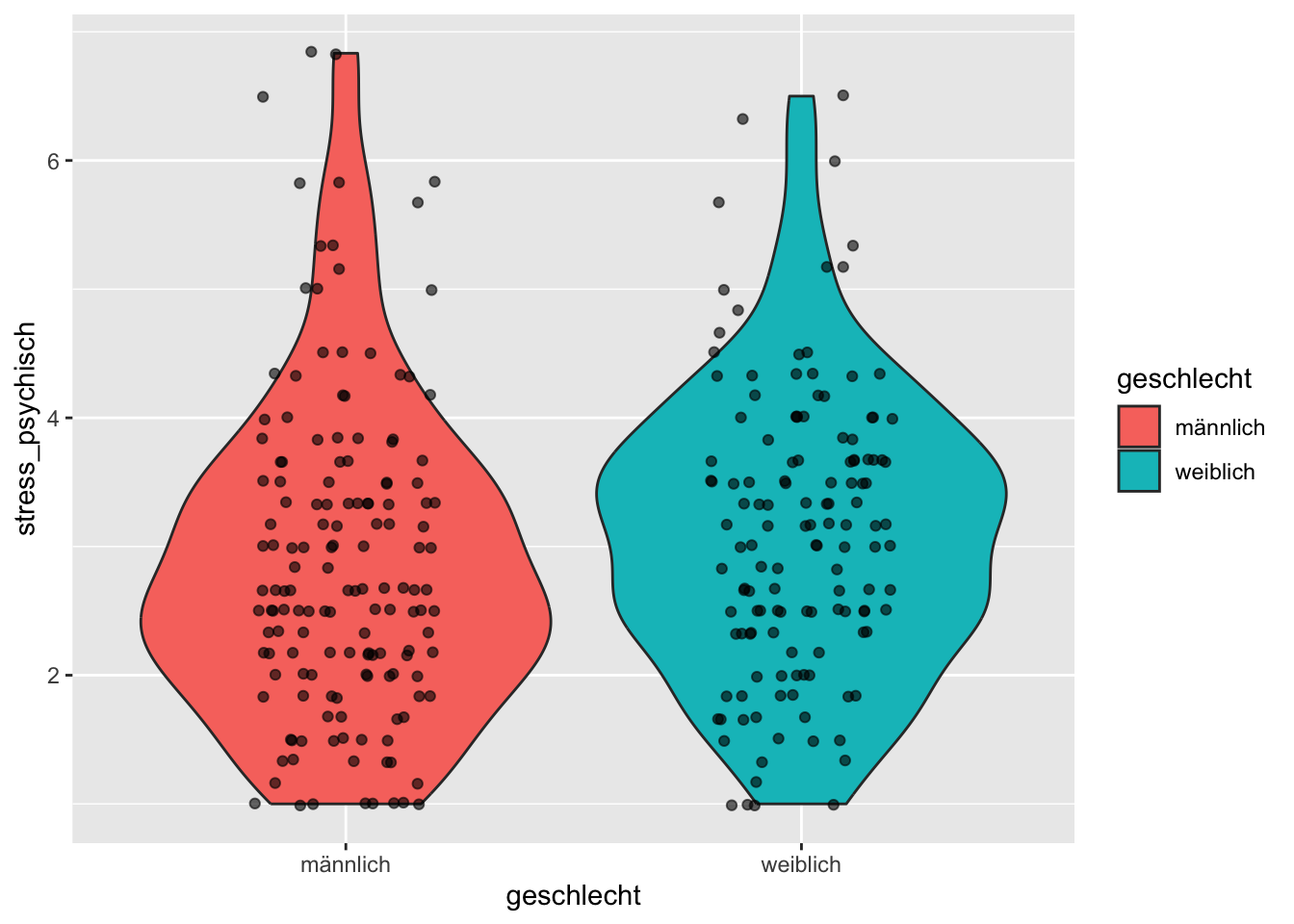
In den bisherigen Beispielen (vgl. Kapitel 3) haben wir kein Plot-Objekt erstellt, sondern den Datensatz mit dem pipe Operator an die ggplot() Funktion geschickt, und dann mit + direkt die geoms hinzugefügt. Die Erstellung eines Plot-Objekts p ist also nicht zwingend notwendig, vereinfacht aber die Arbeit mit ggplot2 besonders am Anfang. Ausserdem haben wir weitere Funktionen verwendet, wie z.B. theme_classic(), um den Hintergrund weiss darzustellen. Auf diese zusätzlichen Funktionen kommen wir weiter unten zurück.
stress |>
ggplot(mapping = aes(
x = geschlecht,
y = stress_psychisch,
fill = geschlecht
)) +
geom_violin() +
geom_jitter(width = 0.2, alpha = 0.6) +
theme_classic()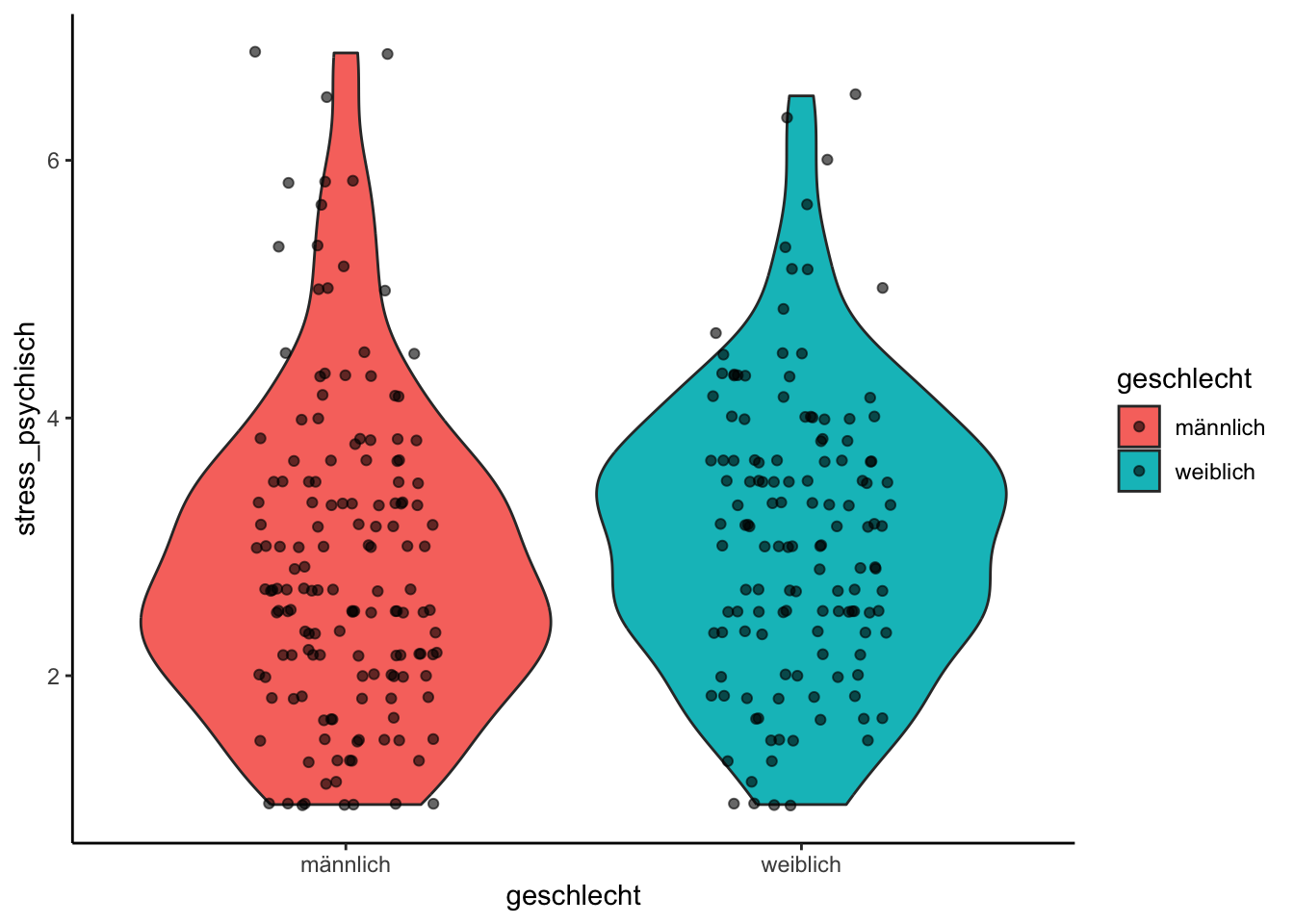
5.4 Geoms für verschiedene Datentypen
Wir fassen zusammen: bisher haben wir gelernt, dass wir einen Plot in mehreren Schritten zusammenstellen. Wir beginnen mit einem Dataframe und definieren mit der ggplot() Funktion ein ggplot2 Objekt. Mit der aes() Funktion weisen wir Variablen eines Dataframes der X-, bzw. der Y-Achse zu und definieren weitere aesthetic mappings, z.B. eine farbliche Codierung anhand einer Gruppierungsvariablen. Anschliessen fügen wir dem Plot-Objekt Grafikelemente mit geom_ Funktionen als Layers hinzu.
Nun schauen wir uns eine Auswahl an geoms für verschiedene Kombination von Variablen an. Wir können dabei entweder eine Variable auf der X-Achse oder zwei Variablen auf den X- und Y-Achsen darstellen und diese Variablen können entweder kontinuierlich oder kategorial sein.
Für die folgenden Beispiele verwenden wir die Datensätze beispieldaten und kinderwunsch. Während wir beispieldaten schon weiter oben eingelesen haben, müssen wir den Datensatz kinderwunsch.sav noch herunterladen, in unserem data-Ordner abspeichern (kinderwunsch.sav) und anschliessend einlesen:
kinderwunsch <- read_sav("data/kinderwunsch.sav") |>
mutate(geschlecht = haven::as_factor(geschlecht))5.4.1 Eine Variable
Wenn wir nur eine Variable auf der X-Achse grafisch darstellen möchten, müssen wir aber dennoch Werte auf der Y-Achse darstellen. Dies wird oft eine deskriptive Zusammenfassung wie z.B. Häufigkeiten sein.
Kategoriale Variablen
Wenn wir eine kategoriale Variable grafisch darstellen, verwenden wir oft einen bar chart or bar graph. Dieser stellt z.B. Häufigkeiten der verschiedenen Kategorien anhand eines Rechtecks (rectangular bar) dar. Die Funktion, welche dafür verwendet wird, heisst geom_bar().
Als Beispiel wollen wir die Häufigkeiten der vier Bildungsstufen des Vaters plotten.
p <- beispieldaten |>
select(bildung_vater) |>
drop_na() |>
ggplot(aes(x = bildung_vater))
p + geom_bar(fill = "lightblue", color = "black")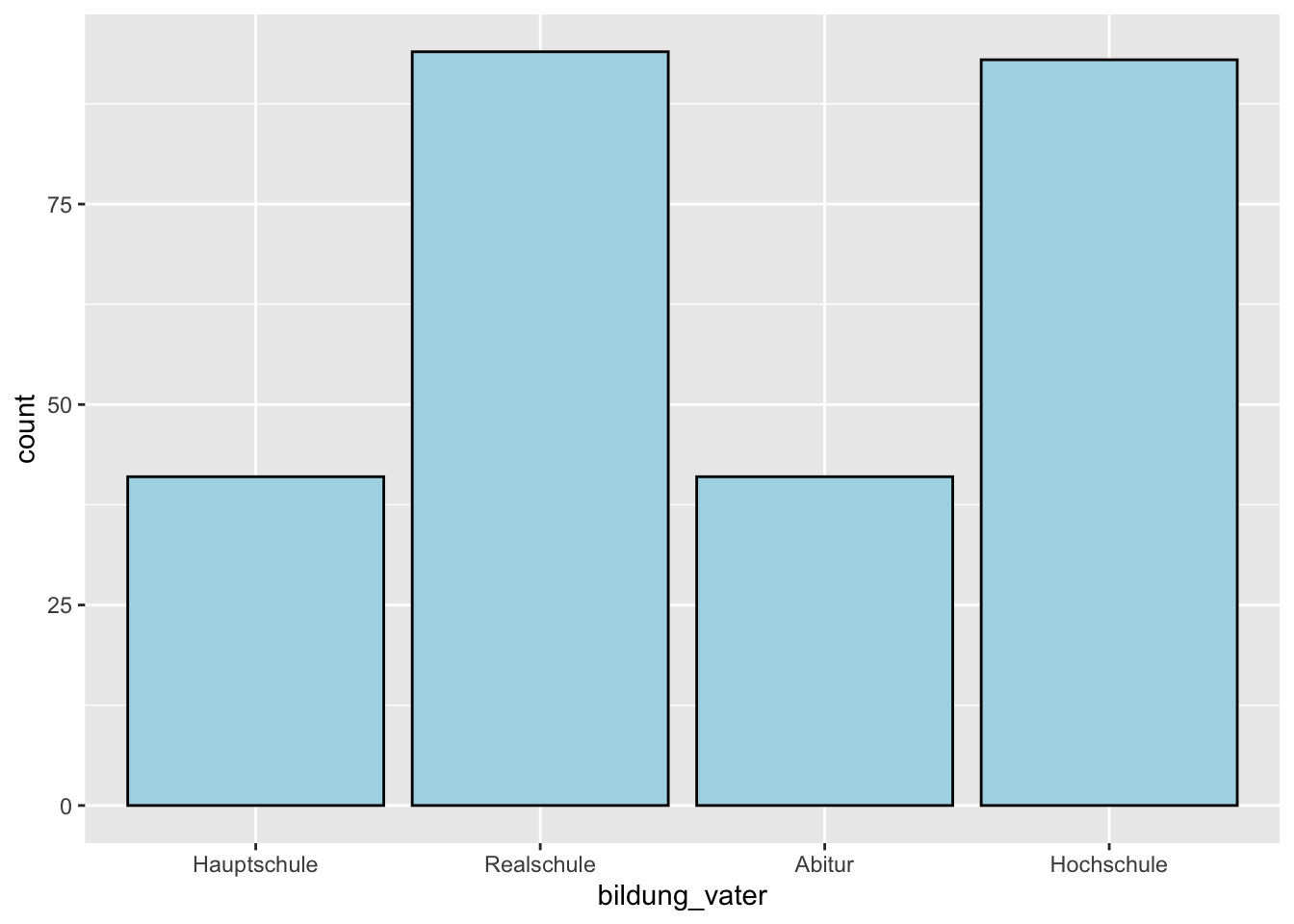
Eine Übersicht über die möglichen Farbnamen erhalten Sie mit der Funktion colors(). Es gibt 657 davon, wir zeigen hier mit sample(15) nur 15 zufällig ausgewählte an:
colors() |> sample(15) [1] "azure1" "gray18" "cornsilk2" "lightsalmon"
[5] "white" "yellow" "salmon1" "grey1"
[9] "darkseagreen2" "gainsboro" "darkslategray1" "gray30"
[13] "grey89" "aquamarine1" "seagreen1" Auch hier können wir zusätzlich eine Gruppierungsvariable angeben, anhand derer wir die Rechtecke farblich kodieren.
p <- beispieldaten |>
select(bildung_vater, westost) |>
drop_na() |>
ggplot(aes(x = bildung_vater, fill = westost))
p + geom_bar()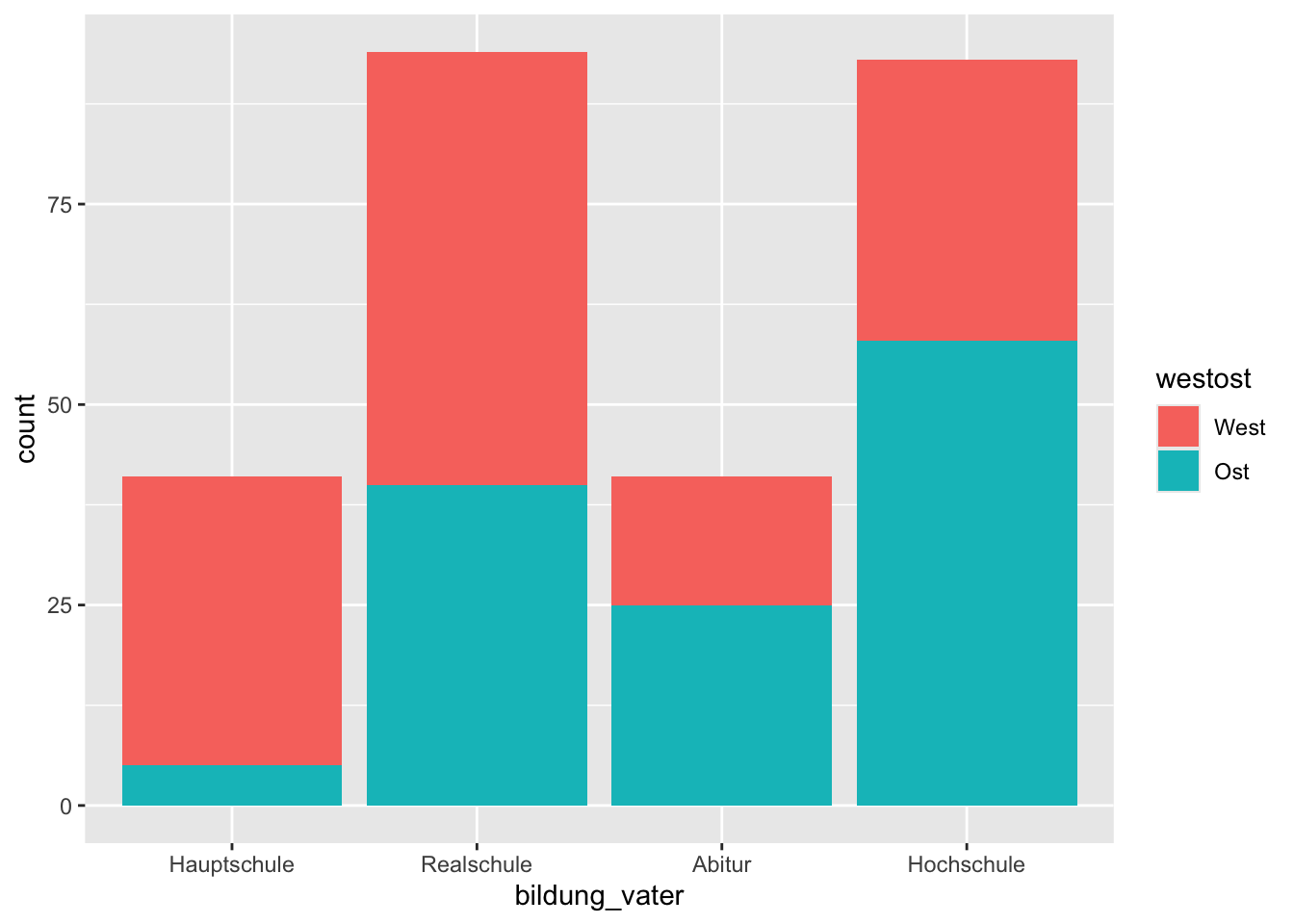
Standardmässig kreiert ggplot2 einen stacked Bar Chart, d.h. die Rechtecke werden aufeinander gestapelt. Wenn dies nicht erwünscht ist, können wir das Argument position = "dodge" der Funktion geom_bar() verwenden. Damit teilen wir mit, dass die Bars nebeneinander gezeichnet werden sollen.
p + geom_bar(position = "dodge")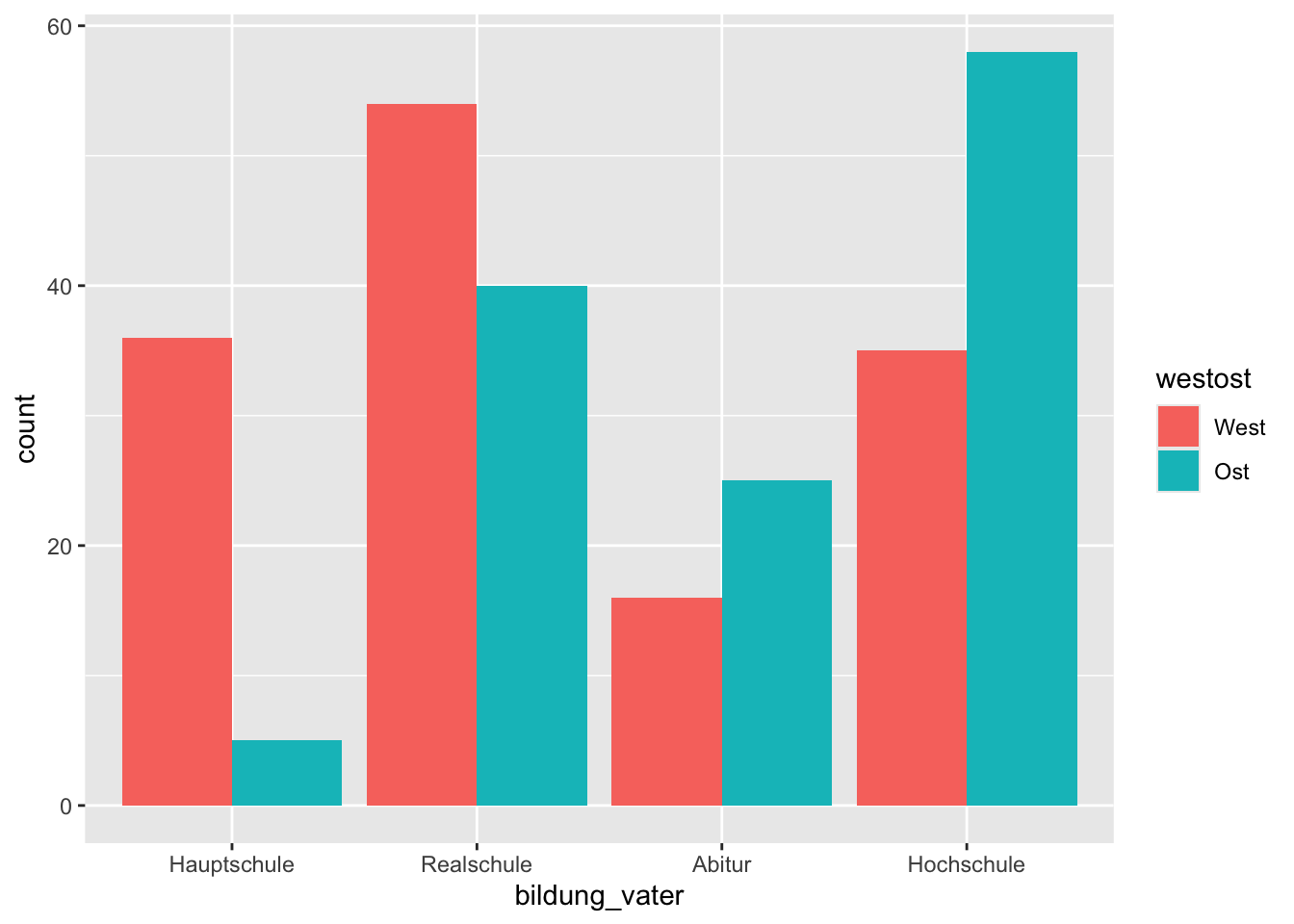
Als dritte Variante können wir position = "identity" verwenden; so werden die Bars übereinander gezeichnet. Da das hintere Rechteck nicht mehr sichtbar ist, verwenden wir das alpha Argument, um die Bars transparent zu machen.
p + geom_bar(position = "identity", alpha = 0.6)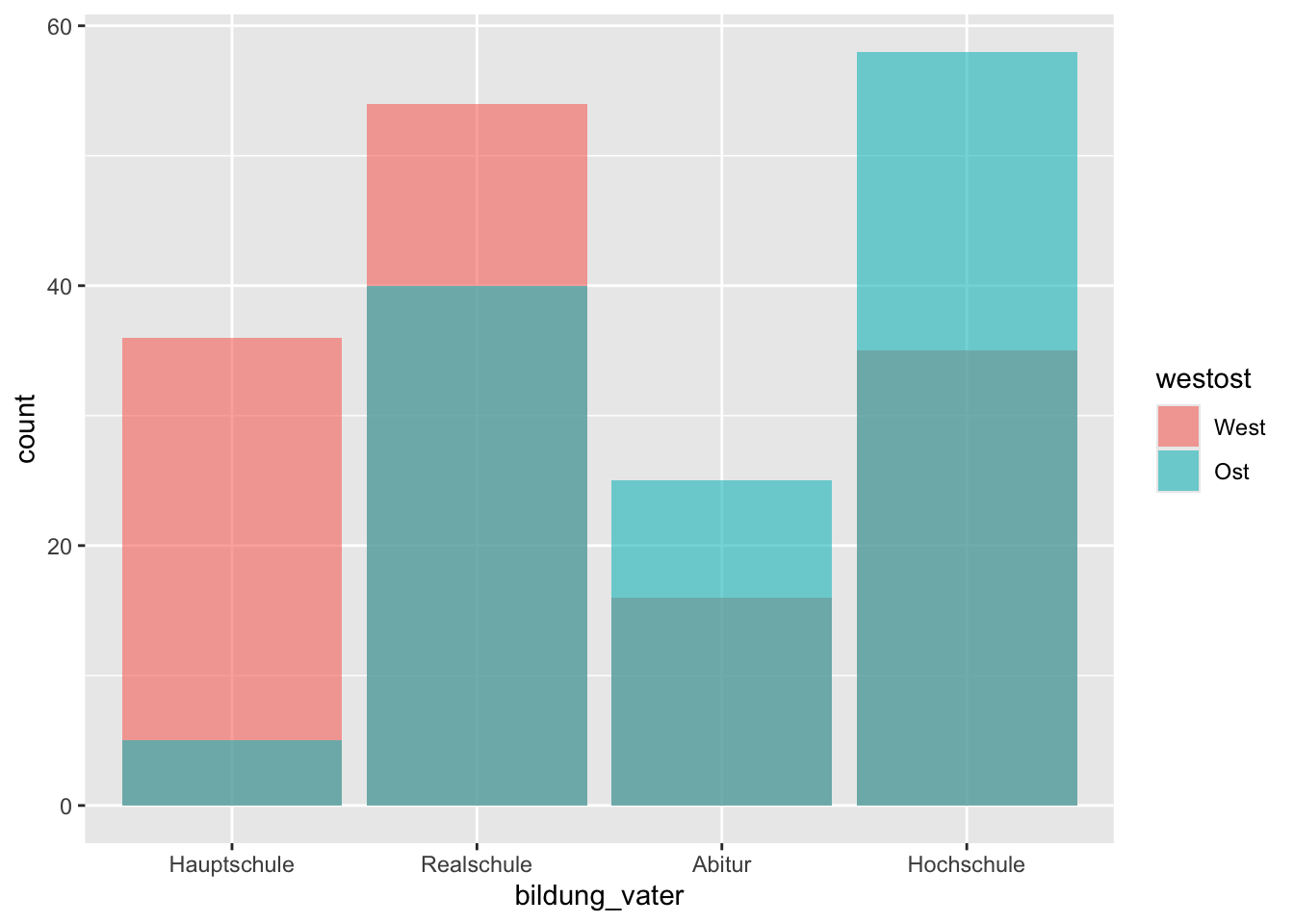
Kontinuierliche Variablen
Falls die Variable, welche wir grafisch darstellen wollen, nicht kategorial, sondern kontinuierlich ist, bietet sich ein Histogramm an; dies erzeugen wir mit der Funktion geom_histogram(). Als Beispiel betrachten wir den psychischen Stress.
Ein Histogramm bietet eine grafische Darstellung der Verteilung einer numerischen Variablen. Dazu werden die Werte dieser Variablen in diskrete Intervalle, oder bins, unterteilt. Auf der Y-Achse werden dann, analog zu einem Bar Chart, die Häufigkeiten in den jeweiligen Intervallen dargestellt. Die Bestimmung der Grösse der Intervalle (binwidth) ist kritisch. Wenn wir nichts spezifieren, wählt ggplot2 selber eine binwidth aus, aber wir können diese mit dem Argument binwidth auch selber angeben.
Wir verwenden wieder den bereits oben gebildeten Datensatz stress, der nur die Variablen ID, stress_psychisch und geschlecht beinhaltet:
p <- stress |>
ggplot(mapping = aes(x = stress_psychisch))
# Wir lassen die binwidth automatisch auswählen
p + geom_histogram()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.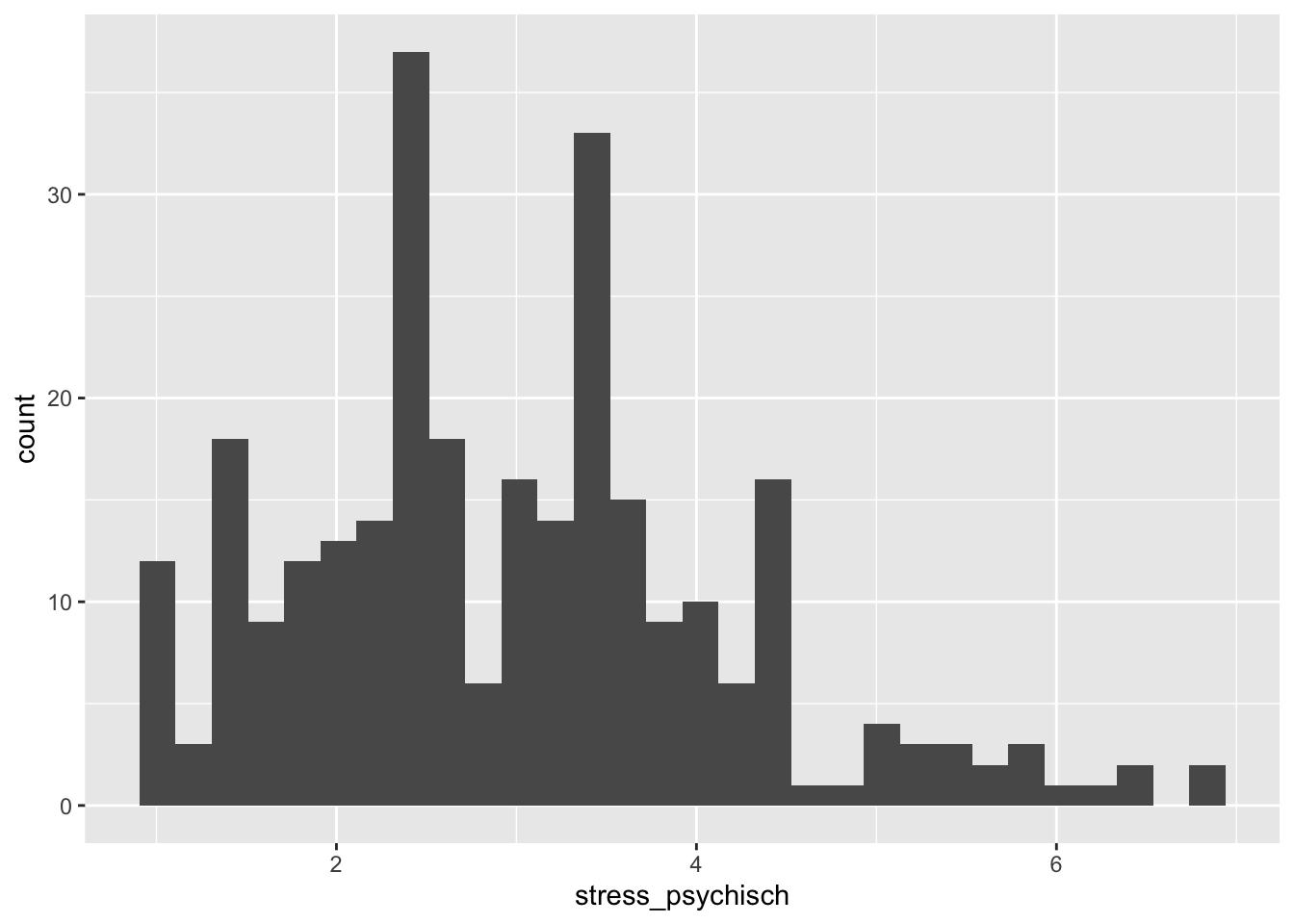
# Wir bestimmen die binwidth selber
p + geom_histogram(binwidth = 0.5)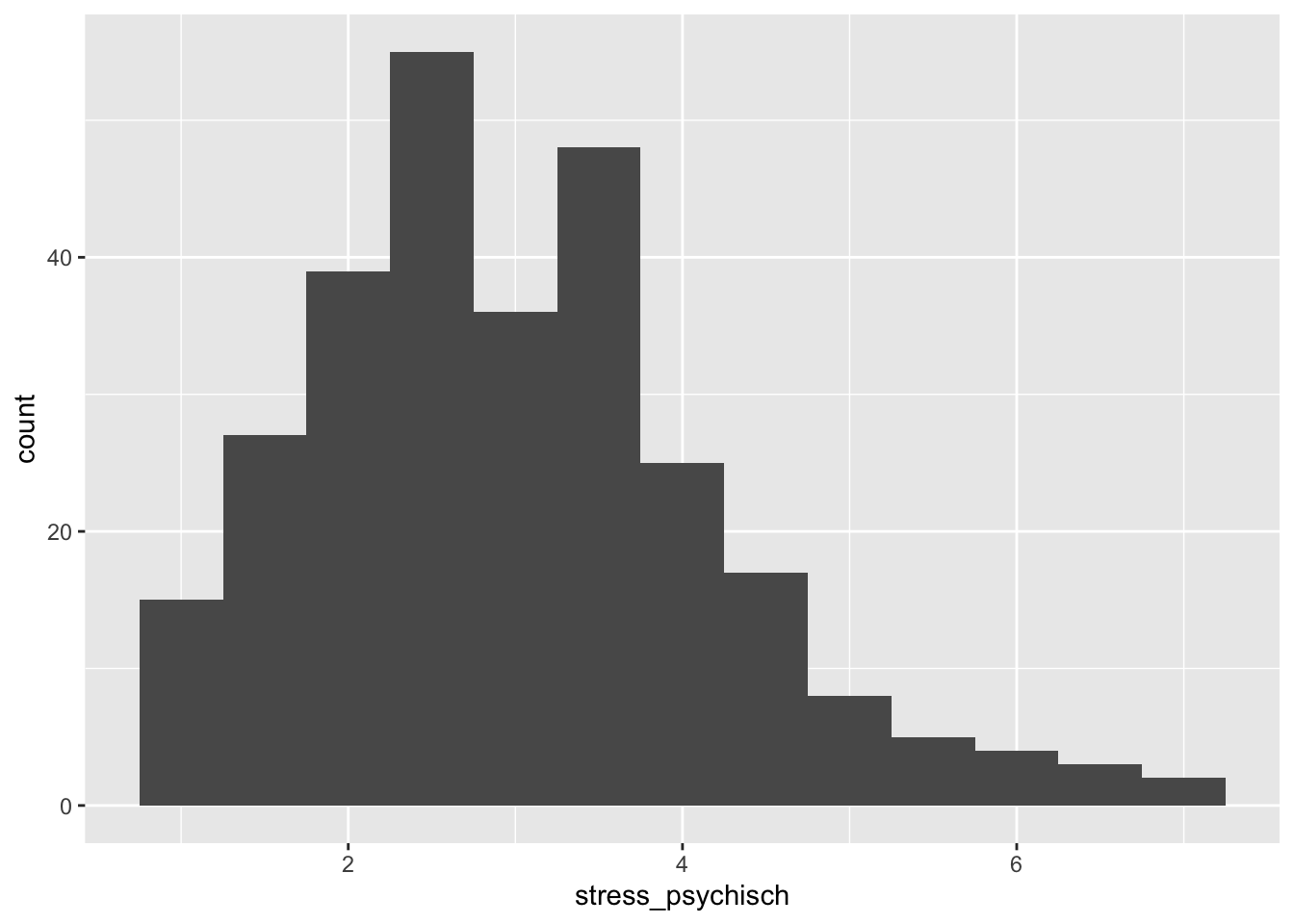
Die Bestimmung der binwidth hängt natürlich von der Skala der Variablen ab und sollte weder zu fein noch zu grob sein.
Statt der binwidth kann mit bins auch die Anzahl der insgesamt zu bildenden Bins angegeben werden:
p + geom_histogram(bins = 20)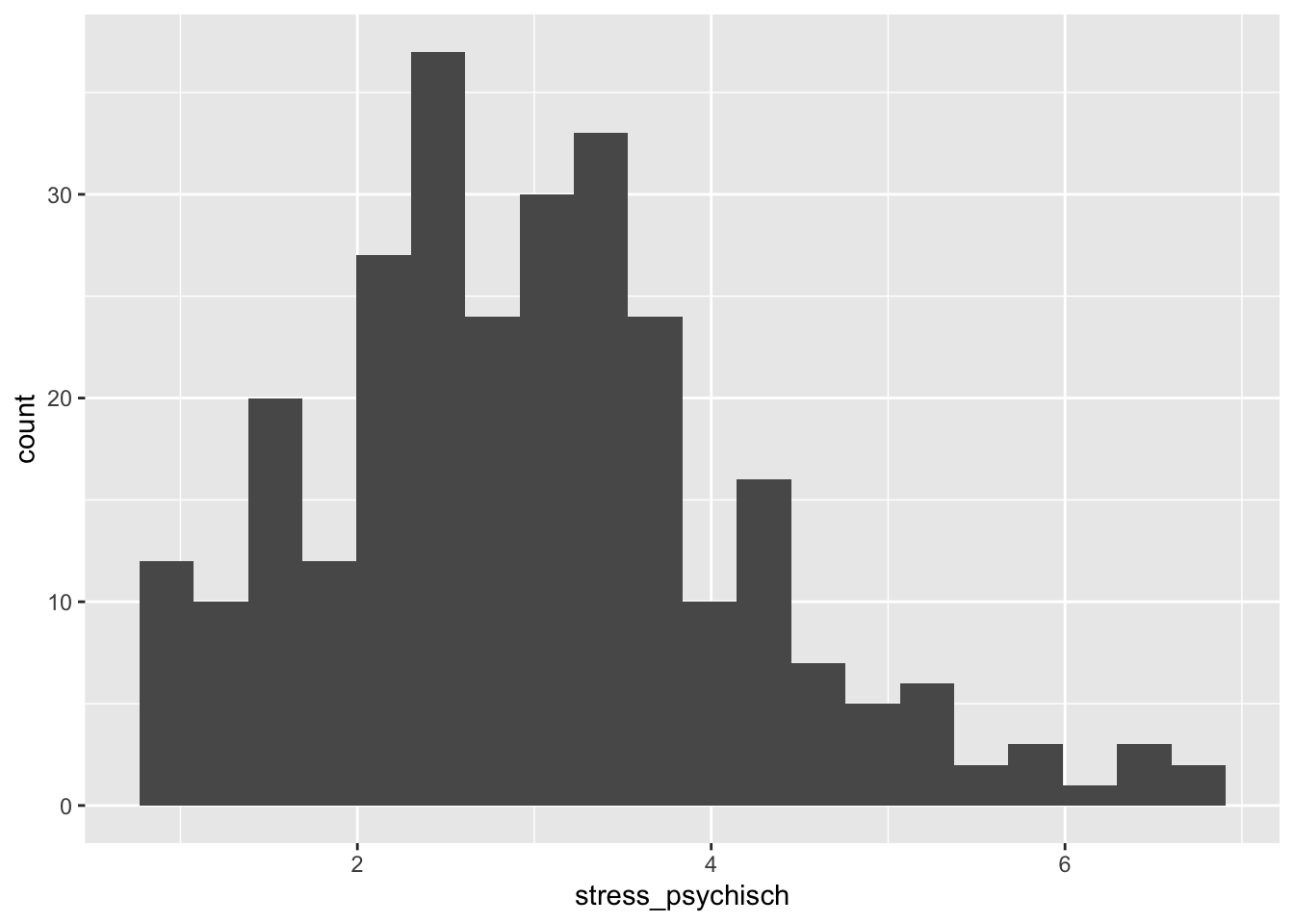
Wenn wir auf der Y-Achse anstelle der absoluten die relativen Häufigkeiten sehen wollen, können wir y = after_stat(density) als Argument der aes() Funktion verwenden.
p + geom_histogram(binwidth = 0.5, aes(y = after_stat(density)))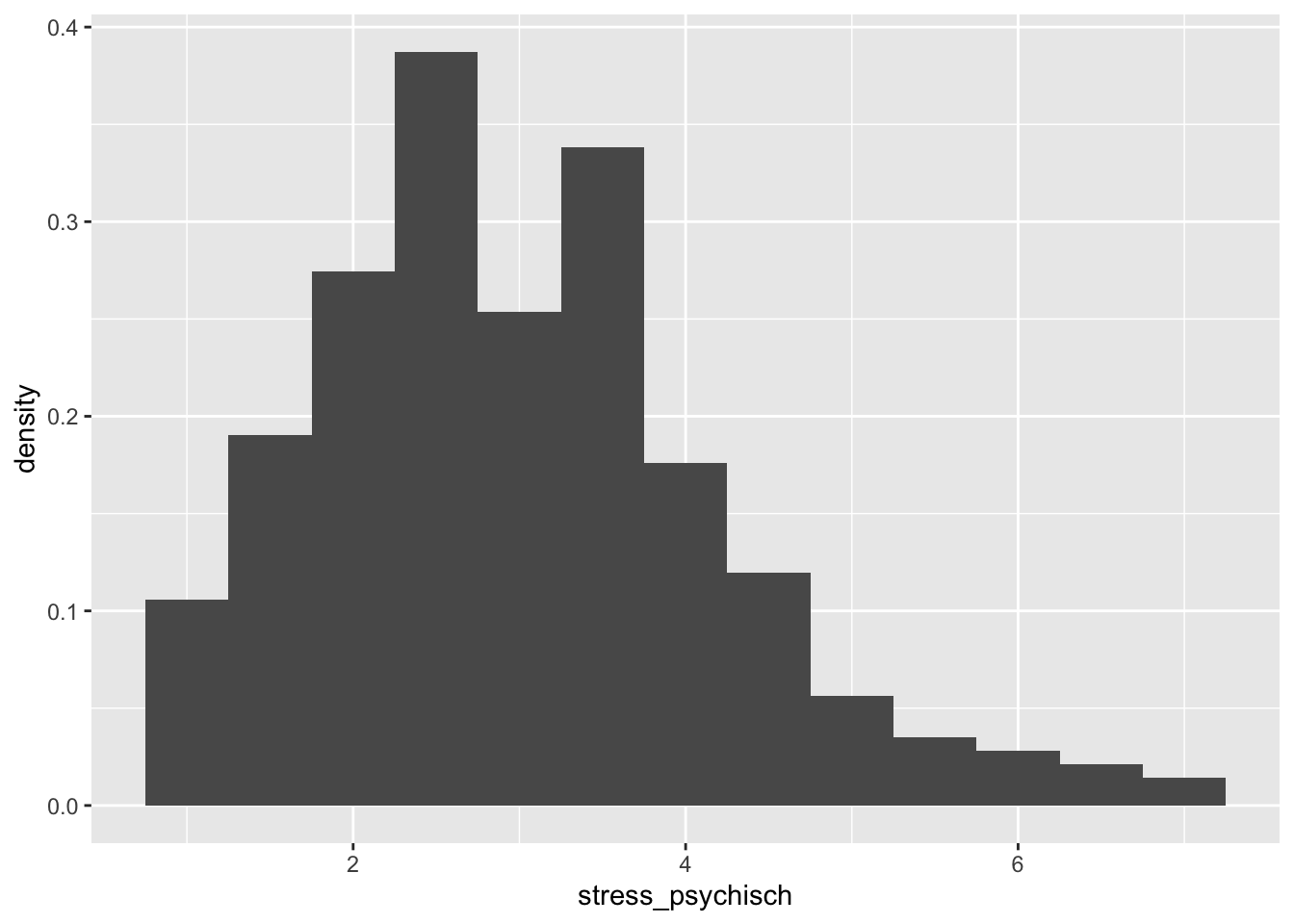
Selbsverständlich gibt es auch für Histogramme die Möglichkeit, einen Faktor als Gruppierungsvariable zu verwenden.
p <- stress |>
ggplot(mapping = aes(x = stress_psychisch, fill = geschlecht))
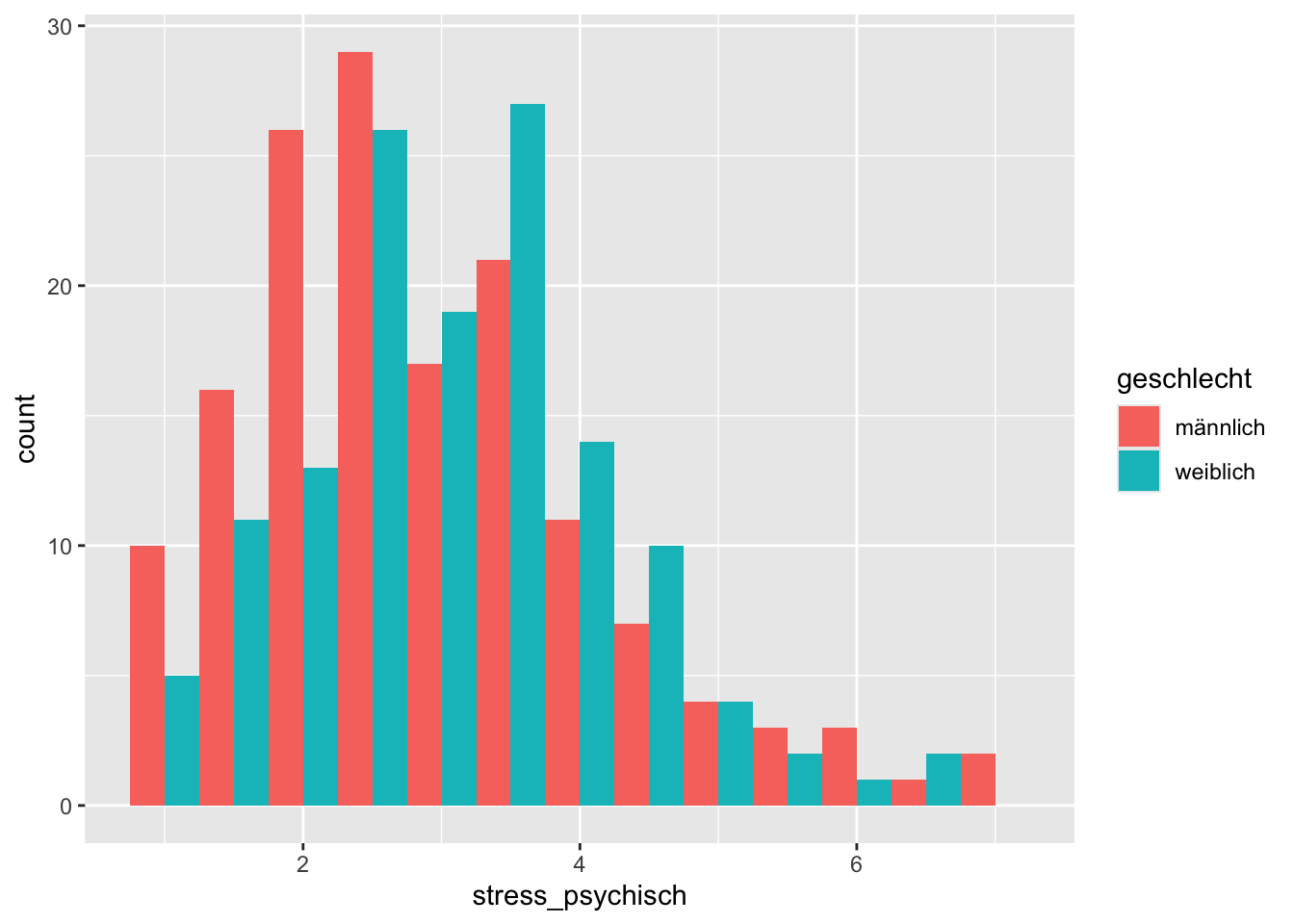
p + geom_histogram(binwidth = 0.5)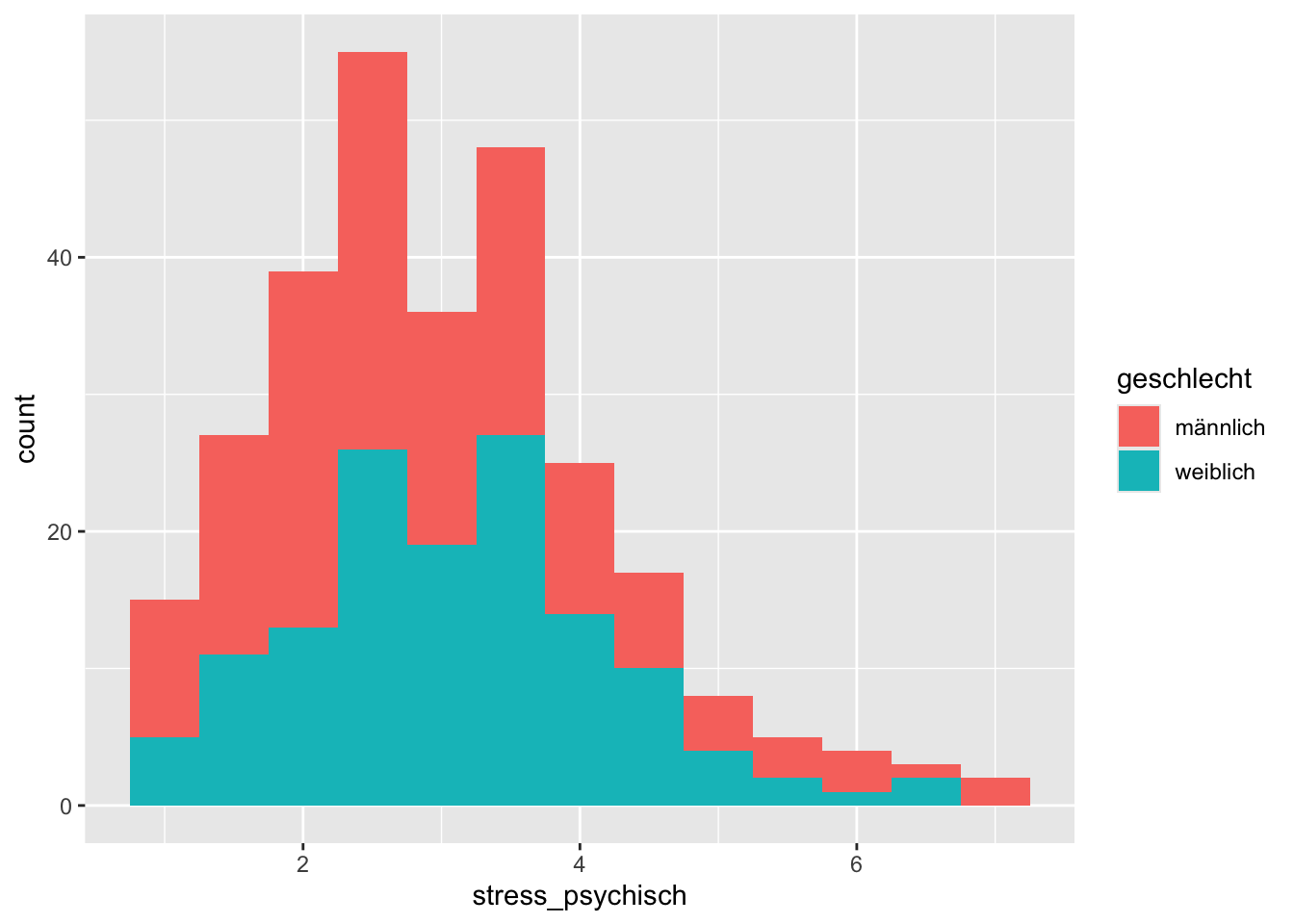
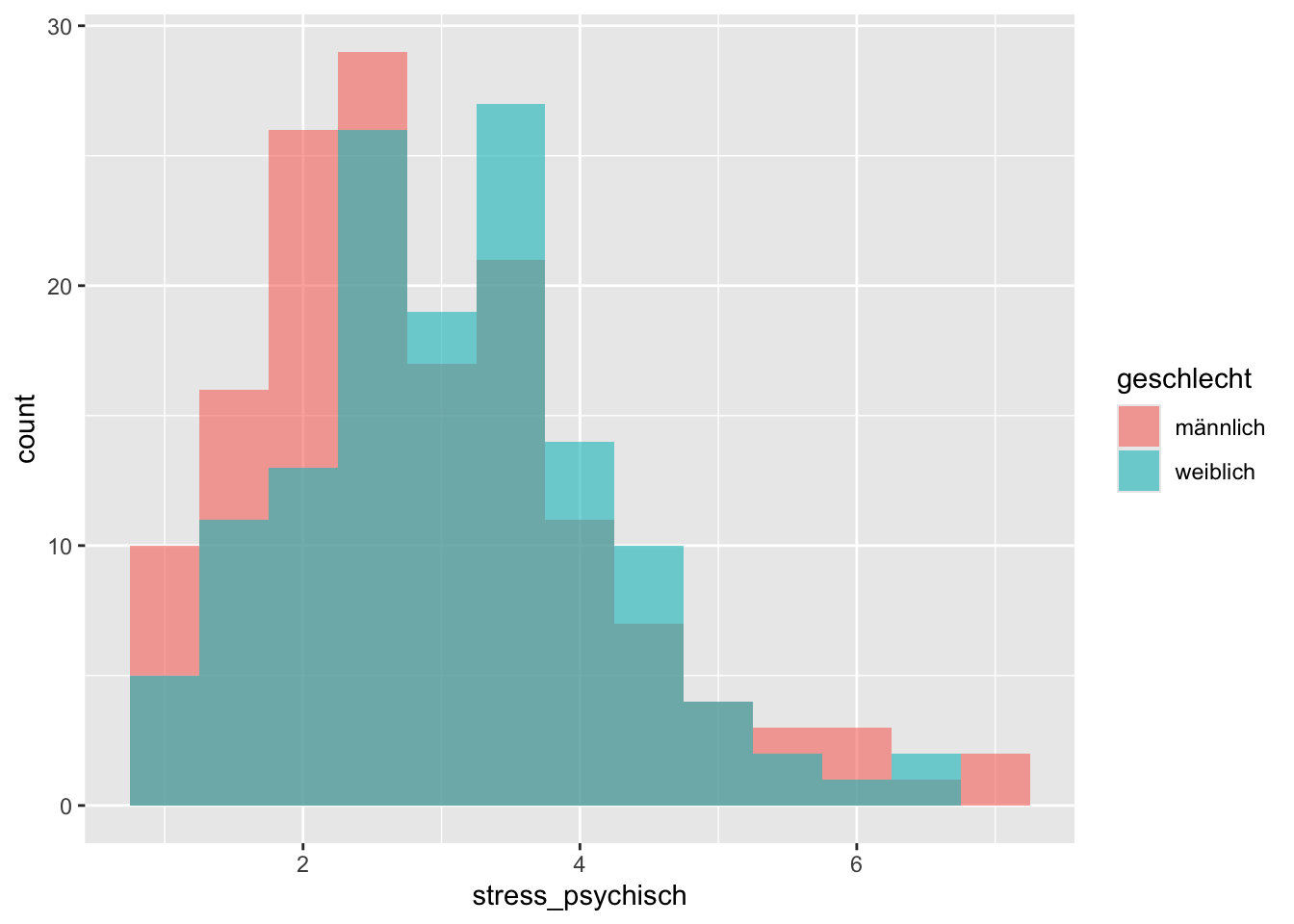
Wie beim Bar Chart werden die Histogramme übereinander (stacked) geplotted. Wollen wir sie aufeinander, verwenden wir position = "identity".
p + geom_histogram(
binwidth = 0.5,
position = "identity",
alpha = 0.6
)
Nebeneinander geht auch:
p + geom_histogram(
binwidth = 0.5,
position = "dodge"
)
Eine gute Alternative zum Histogramm ist ein Density-Plot, den man mit geom_density() erhält. Ein Density-Plot ist eine geglättete (“smoothed”) Version eines Histogramms mit kernel density estimates, also mit geglätteten relativen Häufigkeiten. Wir kennen solche Density-Kurven schon vom Violin-Plot weiter oben (dort vertikal und symmetrisch gespiegelt dargestellt). Ein Density-Plot hat den Vorteil, dass die als kontinuierlich/stetig angenommene Variable stress_psychisch auch in einer kontinuierlichen Form dargestellt wird.
Hier gleich mit dem Plot-Objekt von oben, also getrennt für die beiden Geschlechter mit unterschiedlich farbigen Füllungen:
p + geom_density()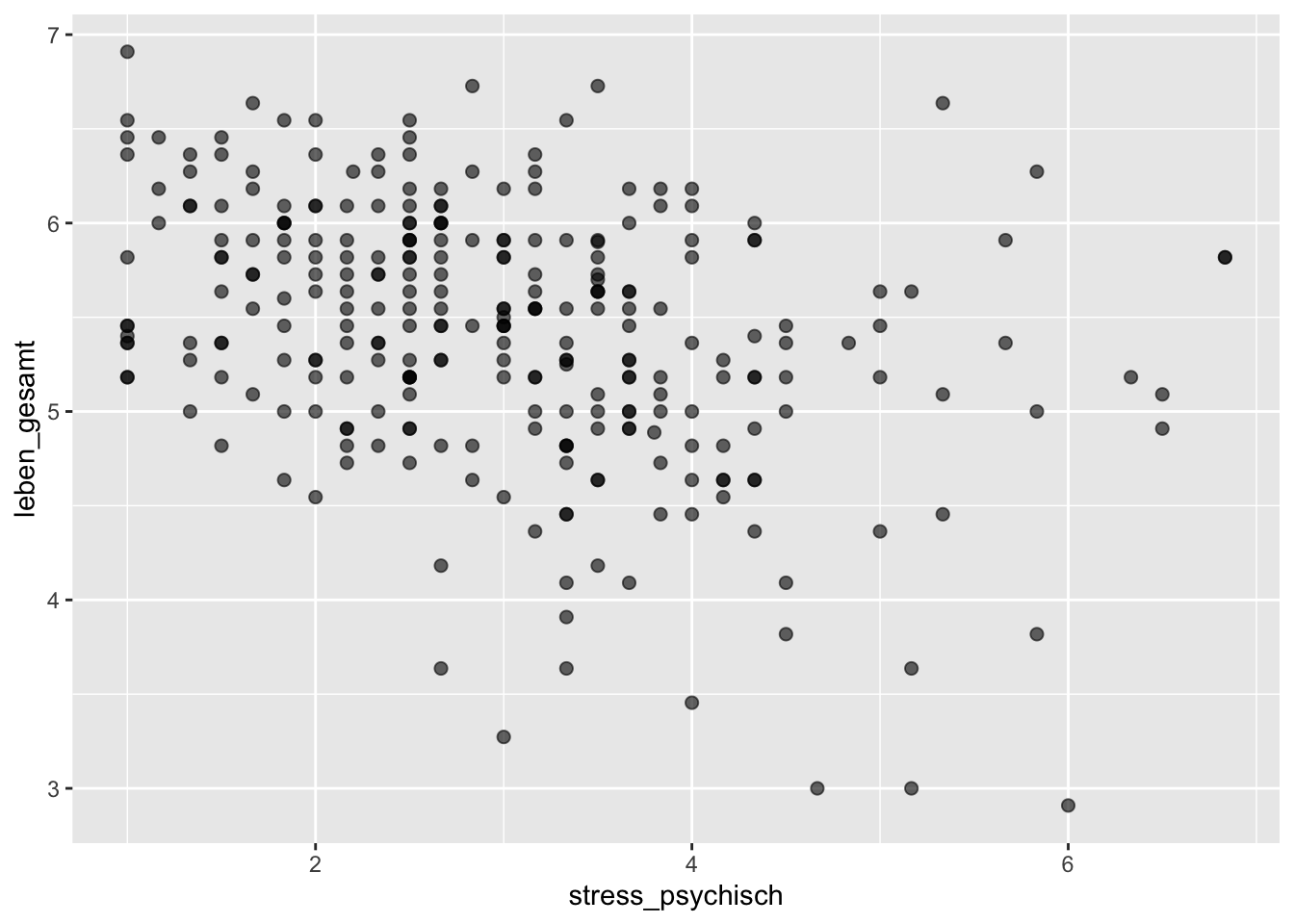
Ein Histogramm kann auch durch eine Density-Kurve ergänzt werden. Hier nochmal das Histogramm für die Gesamtstichprobe (mit aes(y = after_stat(density))) und mit roter Density-Kurve als zweitem Layer:
p <- stress |>
ggplot(mapping = aes(x = stress_psychisch))
p +
geom_histogram(binwidth = 0.5, aes(y = after_stat(density))) +
geom_density(color = "red", size = 1.5)Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth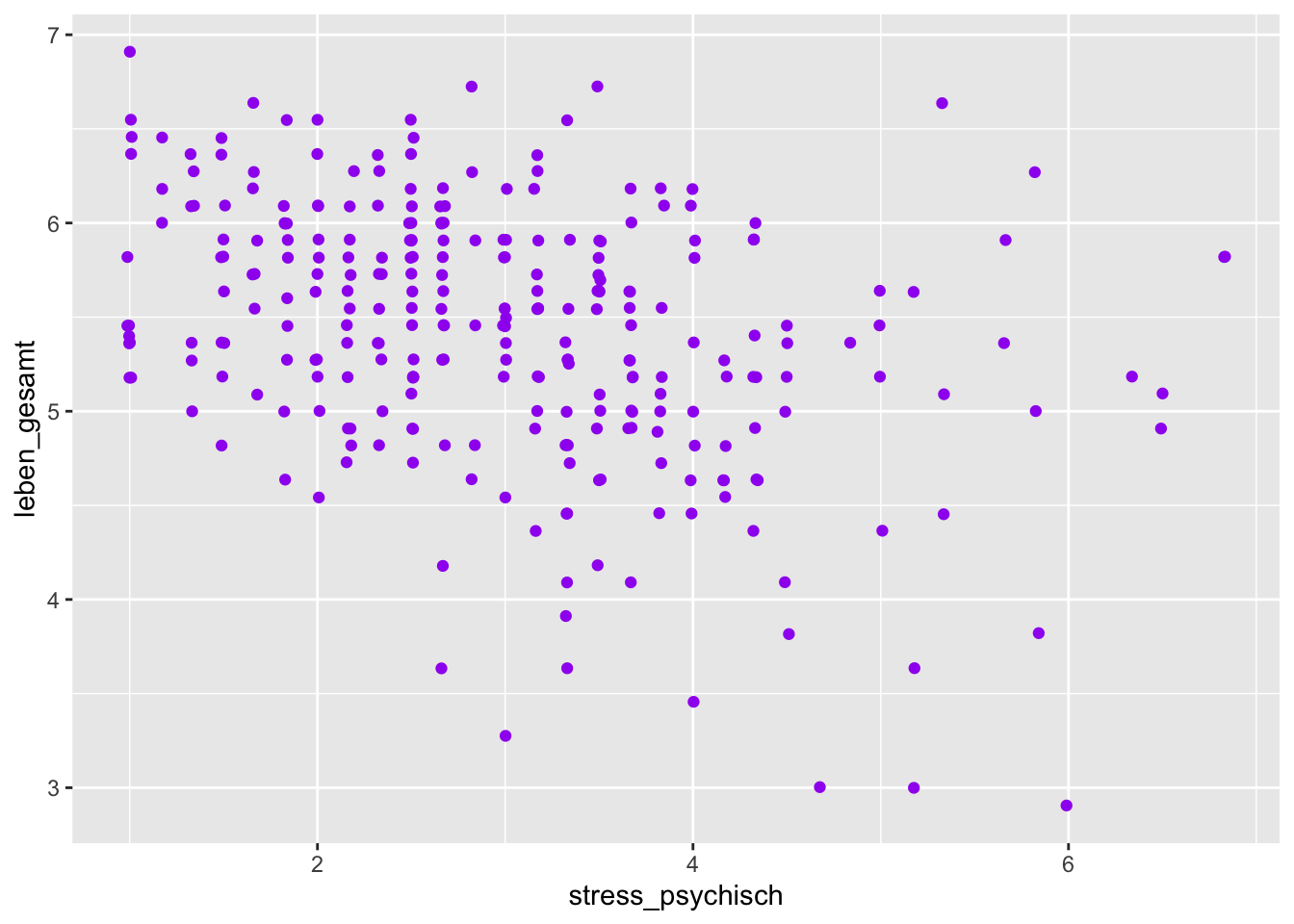` instead.
Die beiden Layer in umgekehrter Reihenfolge zu plotten wäre dagegen nicht optimal:
p +
geom_density(color = "red", size = 1.5) +
geom_histogram(binwidth = 0.5, aes(y = after_stat(density)))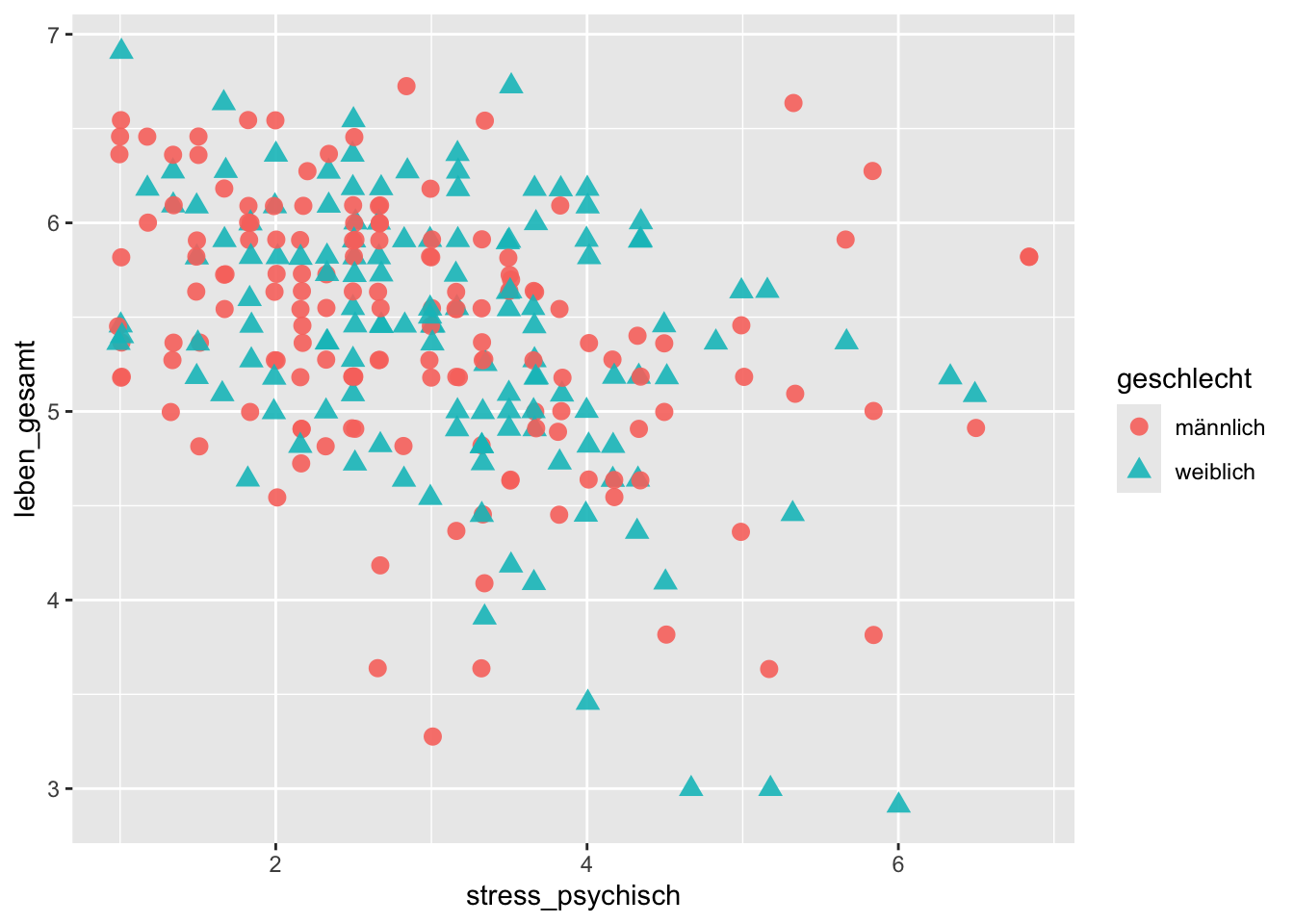
Häufig lässt man sich ein Histogramm ausgeben und legt nicht wie oben die empirische Density-Kurve darüber, sondern eine normalverteilte Kurve (Normalverteilung mit Mittelwert und der Standardabweichung der betreffenden Variable). Dazu verwendet man stat_function() mit den unten angegebenen Argumenten. Auf diese Weise lässt sich die empirische Verteilung der Variable (graues Histogramm) mit der unter einer Annahme einer Normalverteilung erwarteten Kurve vergleichen (rot). Falls die Abweichungen zwischen Histogramm und Kurve sehr gross sind, ist die Normalverteilungsannahme deutlich verletzt.
p +
geom_histogram(binwidth = 0.5, aes(y = after_stat(density))) +
stat_function(fun = dnorm,
args = list(mean = mean(stress$stress_psychisch),
sd = sd(stress$stress_psychisch)),
lwd = 1.5,
col = 'red')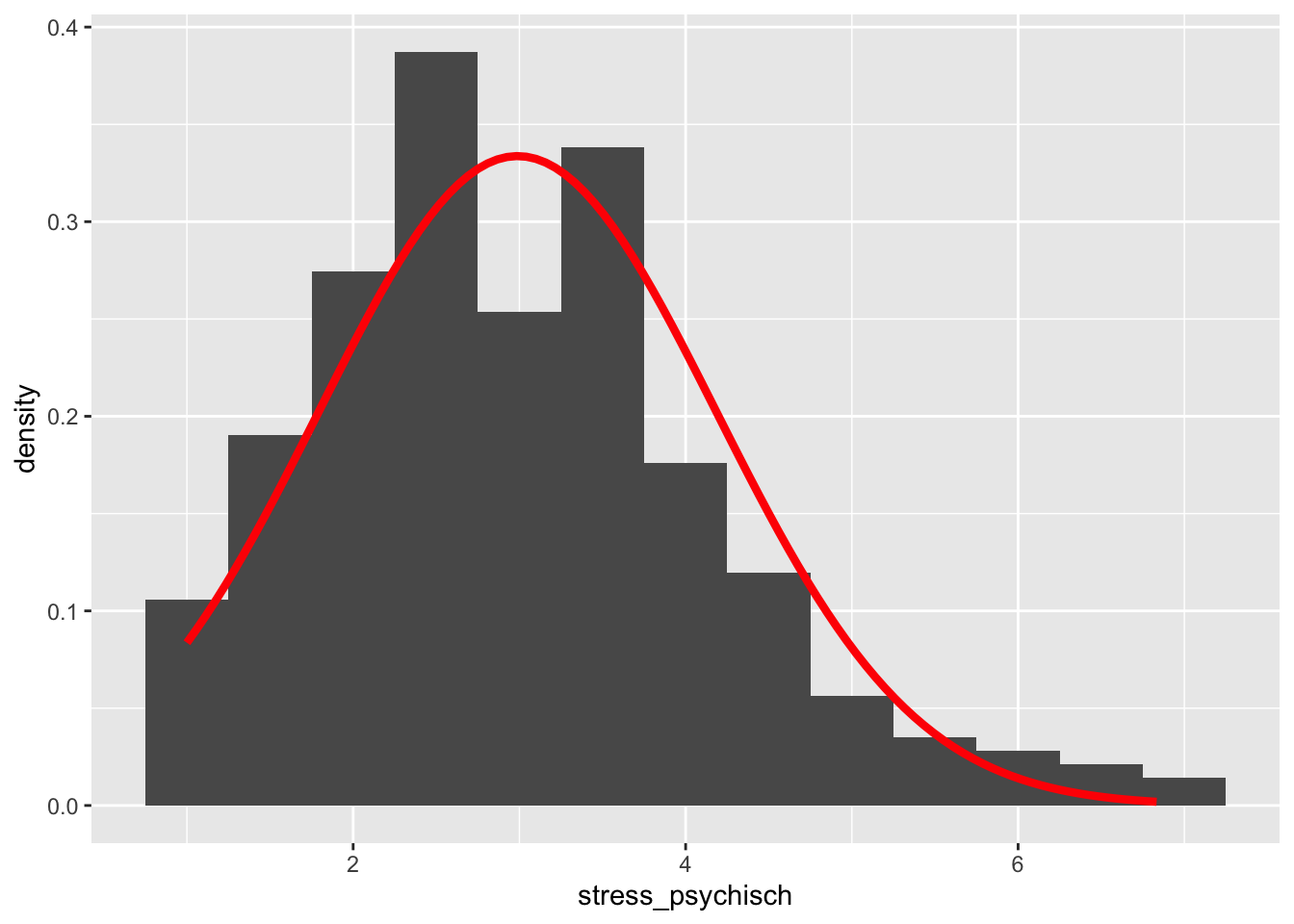
5.4.2 Zwei Variablen
Nun stellen wir zwei Variablen eines Datensatzes gemeinsam dar. Auch hier hängen die möglichen geoms vom Datentyp der Variablen ab.
X und Y kontinuierlich
Wenn beide Variablen kontinuierlich sind, können wir deren Zusammenhang anhand eines ‘Scatterplots’ oder eines Liniendiagrams darstellen. Wir verwenden die Funktionen geom_point(), bzw. geom_line().
Als Beispiel wollen wir den Zusammenhang zwischen psychischem Stress und Lebenszufriedenheit visualisieren.
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt) |>
drop_na() |>
ggplot(mapping = aes(x = stress_psychisch, y = leben_gesamt))
p + geom_point(size = 2, alpha = 0.6)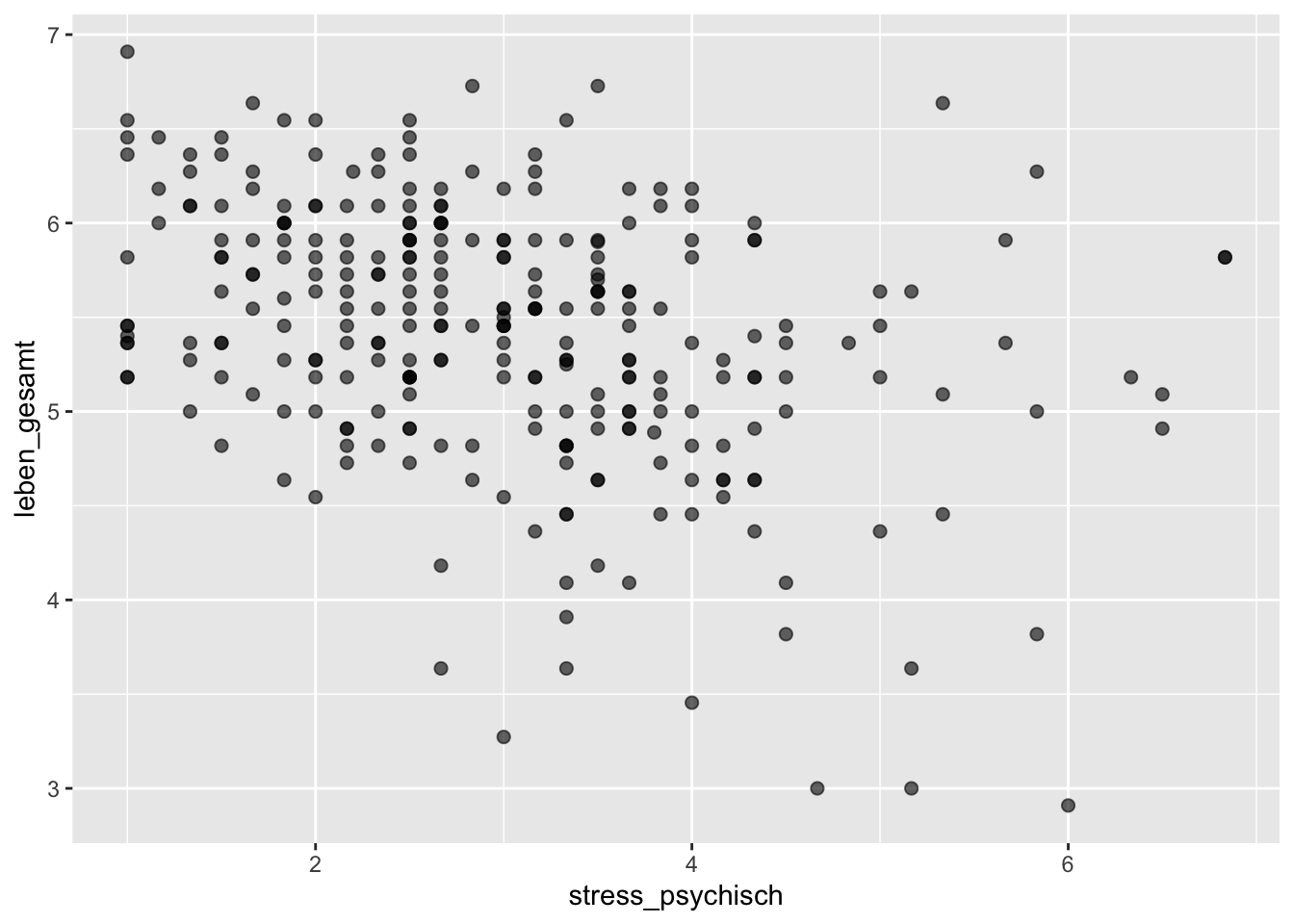
Die size und alpha Argumente haben wir weiter oben bereits kennengelernt, sowie die Möglichkeit, ‘overplotting’ mit der Funktion geom_jitter() zu vermeiden. Sowohl geom_jitter() als auch geom_point() haben auch eine colour oder ein color Argument.
p + geom_jitter(colour = "purple")
Die Gruppierung anhand einer kategorialen Variablen funktioniert auch hier. Wir verwenden sowohl die Farbe als auch die Form der Punkte, um die Kategorien besser unterscheiden zu können.
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt, geschlecht) |>
drop_na() |>
ggplot(mapping = aes(
x = stress_psychisch,
y = leben_gesamt,
color = geschlecht,
shape = geschlecht
))
p + geom_jitter(size = 3, alpha = 0.9)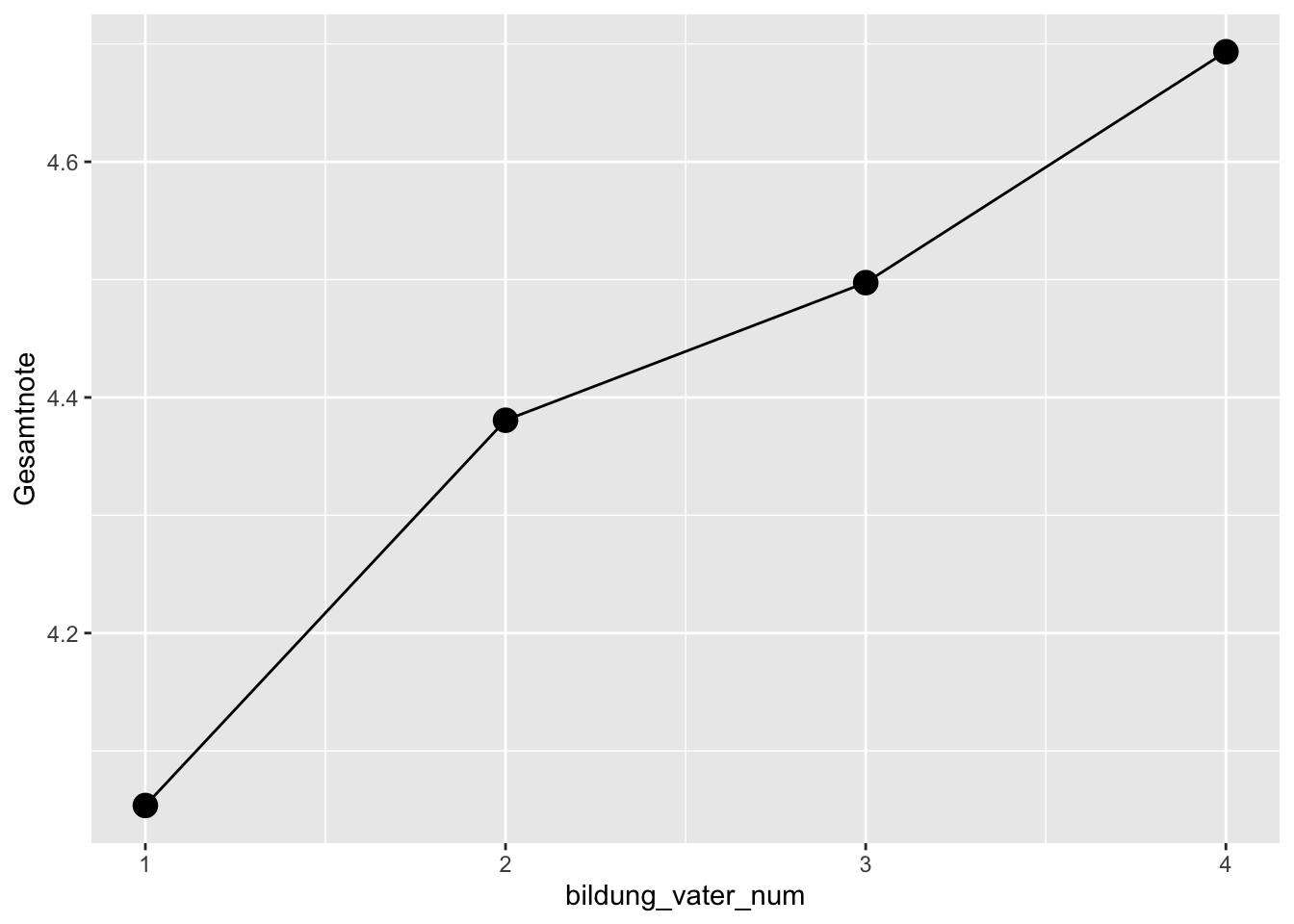
Mit der Funktion geom_line() können wir Liniendiagramme erstellen. Als Beispiel wollen wir in einem neuen Dataframe die Mittelwerte der Gesamtnote der Jugendlichen für die verschiedenen Bildungsniveaus des Vaters berechnen, und dann grafisch darstellen. Bevor wir die Noten-Mittelwerte plotten, konvertieren wir den Faktor bildung_vater zu einer numerischen Variable.
bildung_vater <- beispieldaten |>
select(Gesamtnote, bildung_vater) |>
drop_na() |>
group_by(bildung_vater) |>
summarize(Gesamtnote = mean(Gesamtnote)) |>
mutate(bildung_vater_num = as.numeric(bildung_vater))
bildung_vater# A tibble: 4 × 3
bildung_vater Gesamtnote bildung_vater_num
<fct> <dbl> <dbl>
1 Hauptschule 4.05 1
2 Realschule 4.38 2
3 Abitur 4.50 3
4 Hochschule 4.69 4p <- bildung_vater |>
ggplot(aes(
x = bildung_vater_num,
y = Gesamtnote
))
p + geom_line()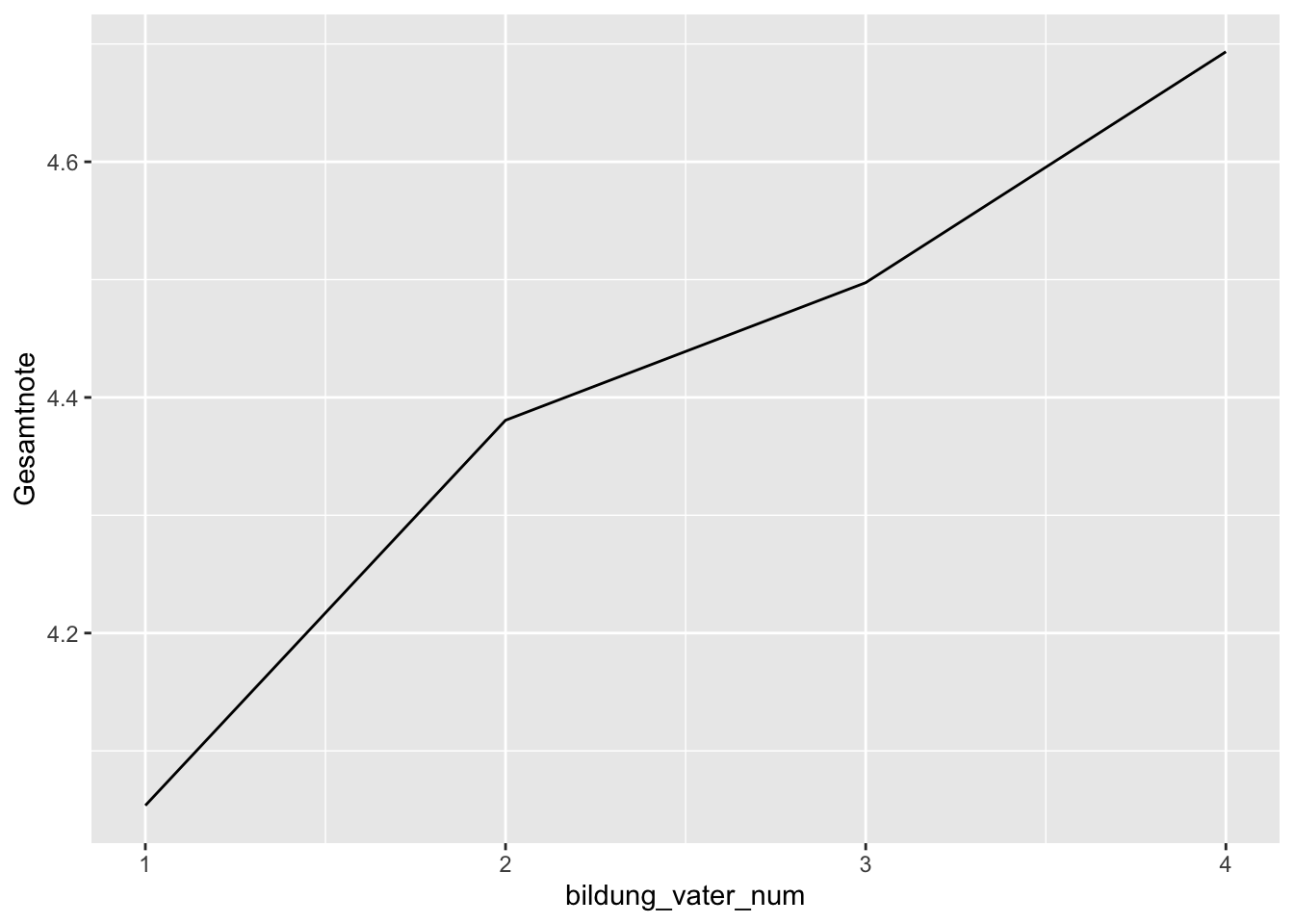
Wir können das Liniendiagramm auch um Punkte ergänzen:
p + geom_line() +
geom_point(size = 4)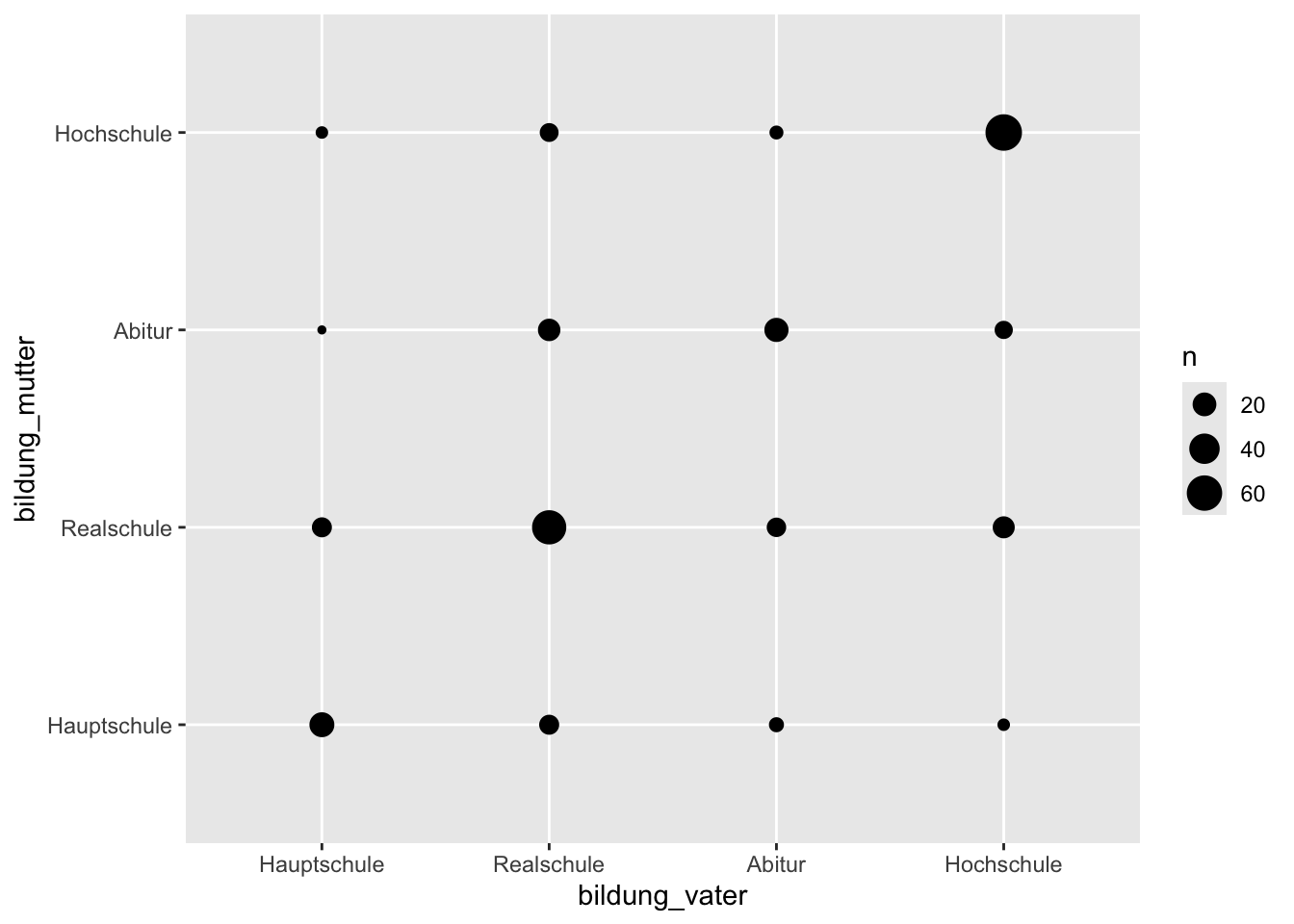
Auch geom_line() hat Argumente, um die Eigenschaften zu ändern. In diesem Fall benützen wir das Argument linteype, welches die Werte "blank", "solid", "dashed", "dotted", "dotdash", "longdash" oder "twodash" anehmen kann.
p + geom_line(linetype = "dashed", linewidth = 2) +
geom_point(size = 8)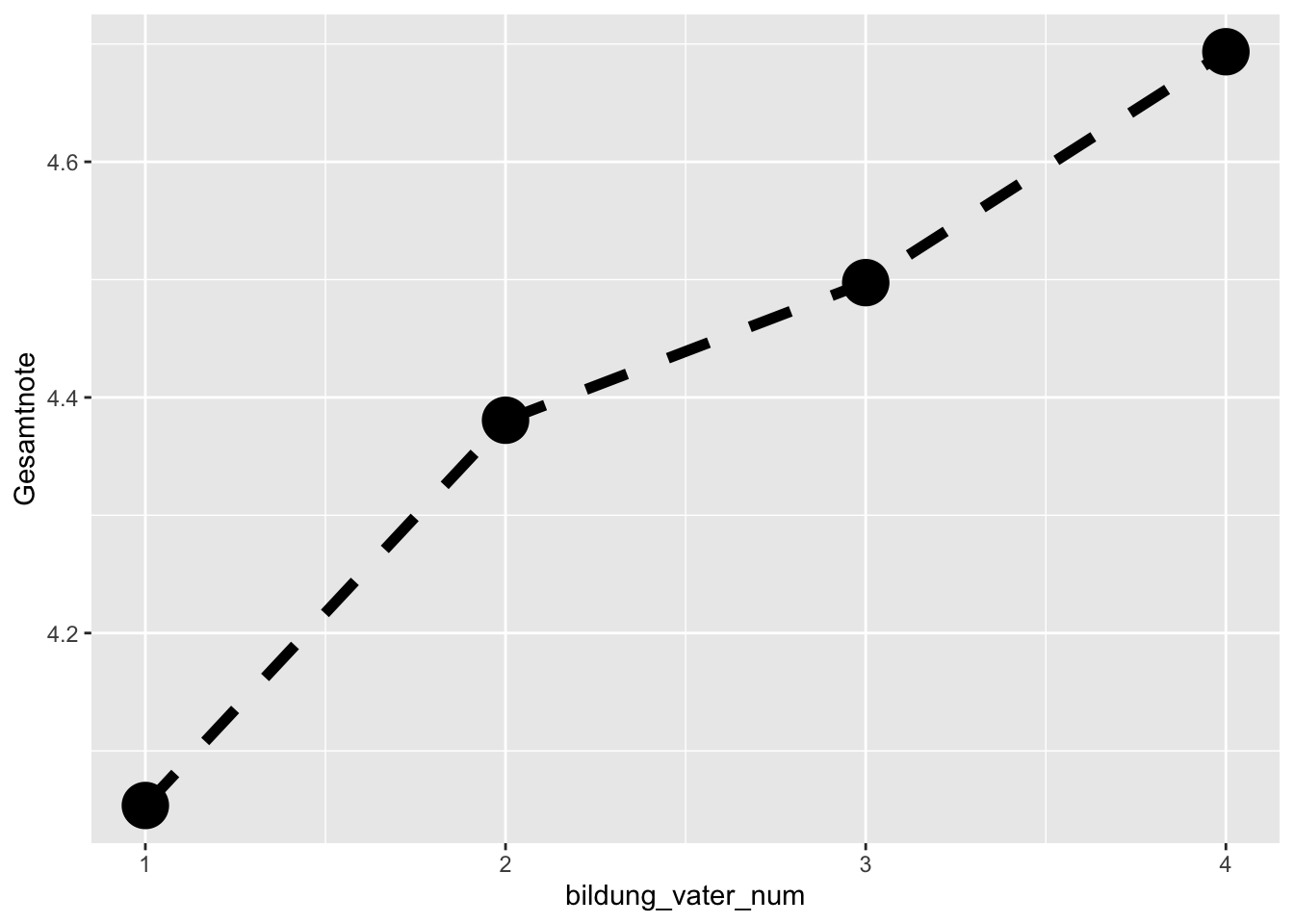
X kategorial und Y kontinuierlich
Wenn eine der Variablen kategorial ist, können wir diese, anstatt sie als Gruppierungsvariable zu verwenden, auf einer Achse darstellen.
Beipiele dafür haben wir oben schon gesehen: dort haben wir die Variablen geschlecht und psychischer Stress dargestellt und die Funktionen geom_boxplot() und geom_violin() benutzt. Wir können aber auch die Funktion geom_bar() für zwei Variablen verwenden. Die Variable auf der Y-Achse wird in diesem Fall für alle Beobachtungen in den Kategieren auf der X-Achse summiert. Da dies keine statistische Transformation benötigt, verwenden wir das Argument stat = 'identity'.
Als Beispiel betrachten wir den Kinderwunsch-Datensatz. In diesem wurden \(n=100\) jugendliche Proband:innen gefragt, ob sie später Kinder haben wollen oder nicht (binäre Antwort). In der Variable kind wurde die Antwort “Nein” (kein Kinderwunsch) wurde mit dem Wert 0 codiert, die Antwort “Ja” (vorhandener Kinderwunsch) mit dem Wert 1. Zusätzlich wurde das Geschlecht der Jugendlichen erhoben. Auf der Y-Achse stellen wir die absoluten Häufigkeiten einer “Ja”-Antwort dar, auf der X-Achse das geschlecht der Jugendlichen.
p <- kinderwunsch |>
ggplot(aes(
x = geschlecht,
y = kind,
fill = geschlecht
))
p + geom_bar(stat = "identity")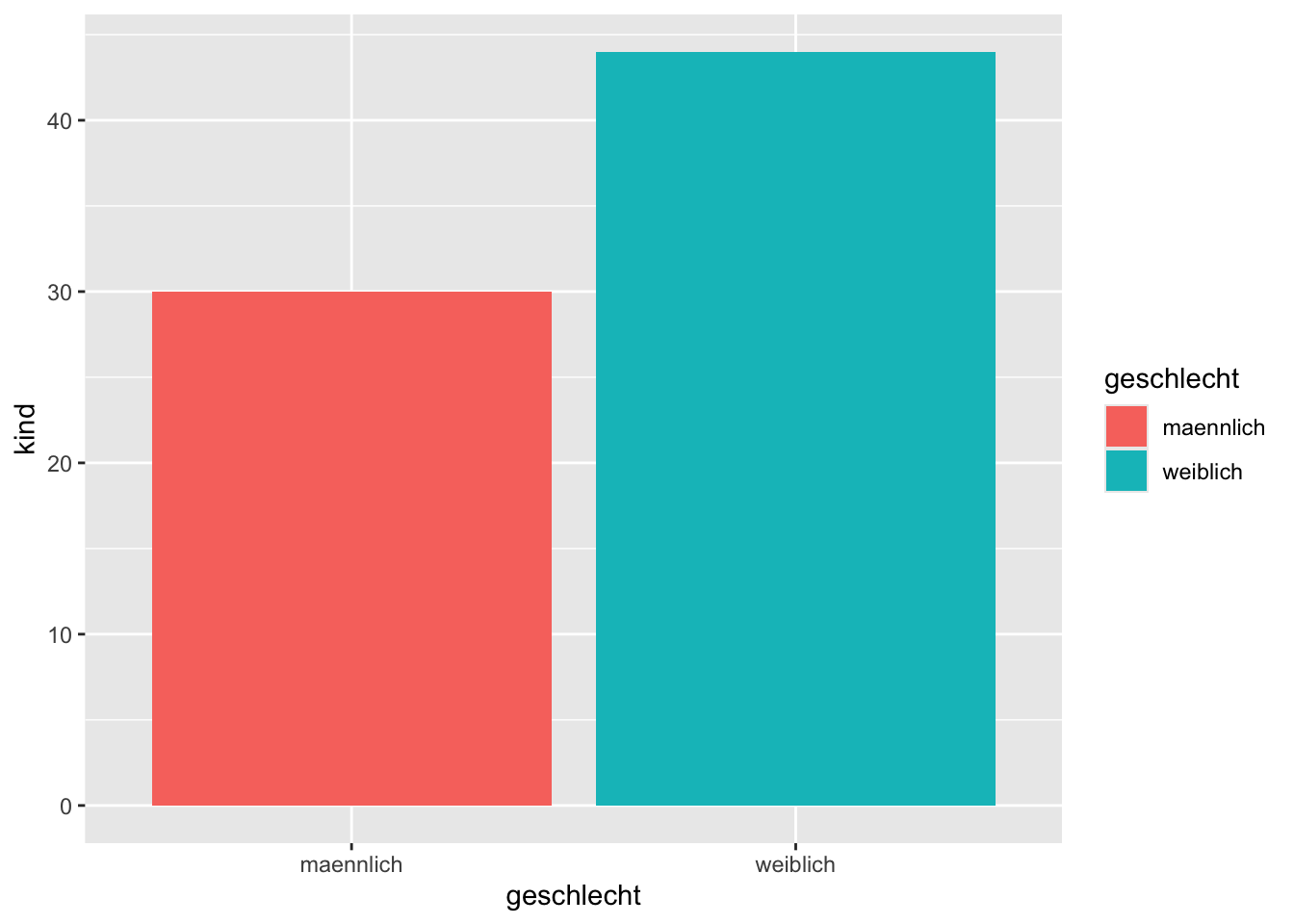
Diese absoluten Häufigkeiten sind allerdings schwer zu interpretieren, da in der Stichprobe nicht gleich viele männliche \((n=44)\) und weibliche \((n=56)\) Jugendliche enthalten sind. Zum besseren Verständnis berechnen wir daher zusätzlich noch die relativen Häufigkeiten einer “Ja”-Antwort pro Geschlecht.
kinderwunsch |>
group_by(geschlecht) |>
summarize(
n = n(),
Ja = sum(kind),
prop_Ja = sum(kind) / n
)# A tibble: 2 × 4
geschlecht n Ja prop_Ja
<fct> <int> <dbl> <dbl>
1 maennlich 44 30 0.682
2 weiblich 56 44 0.786Der Kinderwunsch ist bei weiblichen im Vergleich zu männlichen Jugendlichen also nicht so viel höher ausgeprägt wie es die beiden in der Grafik dargestellten Häufigkeiten vermuten lassen.
X und Y kategorial
Zuletzt können die Variablen sowohl auf der X- als auch auf der Y-Achse kategorial sein. In diesem Fall wäre es sinnvoll, die gemeinsamen Häufigkeiten grafisch darzustellen. Dafür gibt es die Funktion geom_count().
Als Beispiel wollen wir die gemeinsame Häufigkeitsverteilung der Bildung des Vaters und der Bildung der Mutter betrachten.
p <- beispieldaten |>
select(starts_with("bildung")) |>
drop_na() |>
ggplot(aes(
x = bildung_vater,
y = bildung_mutter
))
p + geom_count()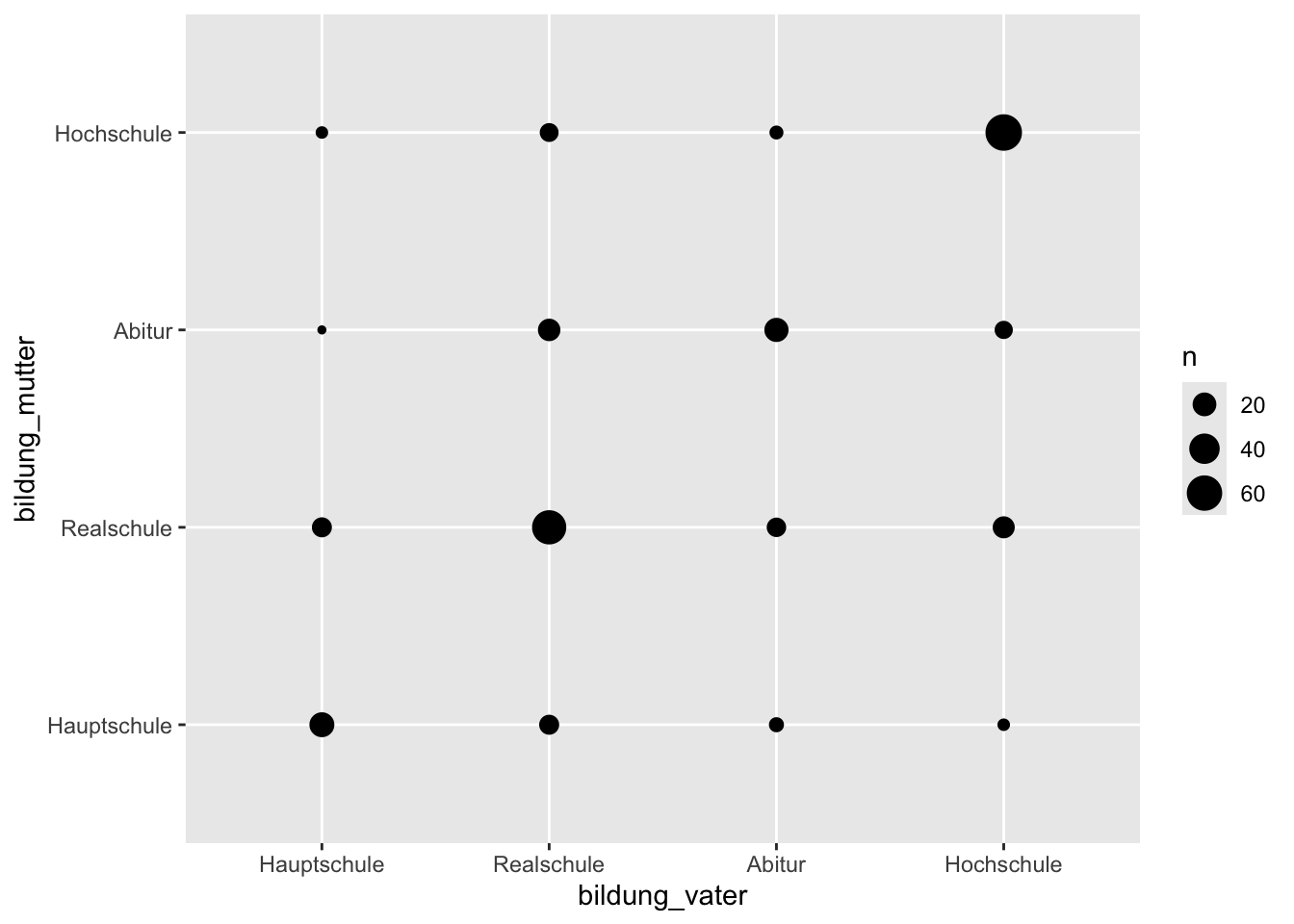
geom_count() zählt die gemeinsamen Häufigkeiten der Kategorien der beiden Variablen und stellt diese als Durchmesser der Punkte dar.
Beispiele
Wir betrachten nun zwei Übungsbeispiele.
Arbeitszufriedenheit im Verlauf
In diesem Beispiel soll der Verlauf der Arbeitszufriedenheit (Skala von 1 bis 15) über die ersten sechs Monate der Anstellung (3 Messzeitpunkte: Anfang, nach 3 Monaten, nach 6 Monaten) zwischen 2 verschiedenen Firmen verglichen werden. In jeder der beiden Firmen wurden jeweils \(n=5\) Angestellte zu ihrer Arbeitszufriedenheit befragt. Es handelt sich um fiktive Daten, die wir zuerst herunterladen und in unserem data-Ordner abspeichern müssen: arbeitszufriedenheit.csv
library(readr)
arbeitszufriedenheit <- read_csv("data/arbeitszufriedenheit.csv", show_col_types = FALSE)
arbeitszufriedenheit# A tibble: 10 × 5
id firma anfang drei_monate sechs_monate
<dbl> <dbl> <dbl> <dbl> <dbl>
1 1 1 9 4 5
2 2 1 9 4 8
3 3 1 9 7 14
4 4 1 10 9 5
5 5 1 8 1 3
6 6 2 10 10 10
7 7 2 9 11 10
8 8 2 10 11 12
9 9 2 12 13 14
10 10 2 9 9 9Die Daten befinden sich im wide Format und müssen daher zunächst ins long Format gebracht werden. Ausserdem müssen die Variablen id und firmanoch zu Faktoren konvertiert werden:
library(tidyverse)
arbeitszufriedenheit_long <- arbeitszufriedenheit |>
pivot_longer(!c(firma, id),
names_to = "messzeitpunkt",
values_to = "arbeitszufriedenheit"
) |>
mutate(id = as.factor(id),
firma = as.factor(firma),
messzeitpunkt = as.factor(messzeitpunkt)
)
arbeitszufriedenheit_long # A tibble: 30 × 4
id firma messzeitpunkt arbeitszufriedenheit
<fct> <fct> <fct> <dbl>
1 1 1 anfang 9
2 1 1 drei_monate 4
3 1 1 sechs_monate 5
4 2 1 anfang 9
5 2 1 drei_monate 4
6 2 1 sechs_monate 8
7 3 1 anfang 9
8 3 1 drei_monate 7
9 3 1 sechs_monate 14
10 4 1 anfang 10
# ℹ 20 more rowsZum Plotten benötigen wir die Mittelwerte der Arbeitszufriedenheit pro firma und messzeitpunkt:
arbeitszufriedenheit_means <- arbeitszufriedenheit_long |>
group_by(firma, messzeitpunkt) |>
summarize(mean_zufrieden = mean(arbeitszufriedenheit))`summarise()` has grouped output by 'firma'. You can override using the
`.groups` argument.arbeitszufriedenheit_means# A tibble: 6 × 3
# Groups: firma [2]
firma messzeitpunkt mean_zufrieden
<fct> <fct> <dbl>
1 1 anfang 9
2 1 drei_monate 5
3 1 sechs_monate 7
4 2 anfang 10
5 2 drei_monate 10.8
6 2 sechs_monate 11 Wir stellen nun anhand eines Liniendiagrams die mittlere Arbeitszufriedenheit über die Messzeitpunkte hinweg dar, mit firma als Gruppierungsfaktor. group = firma ist hier wichtig, die anderen beiden Argumente, color = firma und linetype = firma sind nur aus ästhetischen Gründen da und könnten auch weggelassen werden.
p <- arbeitszufriedenheit_means |>
ggplot(aes(
x = messzeitpunkt,
y = mean_zufrieden,
color = firma,
linetype = firma,
group = firma
))
p + geom_point(size = 4) +
geom_line(linewidth = 2)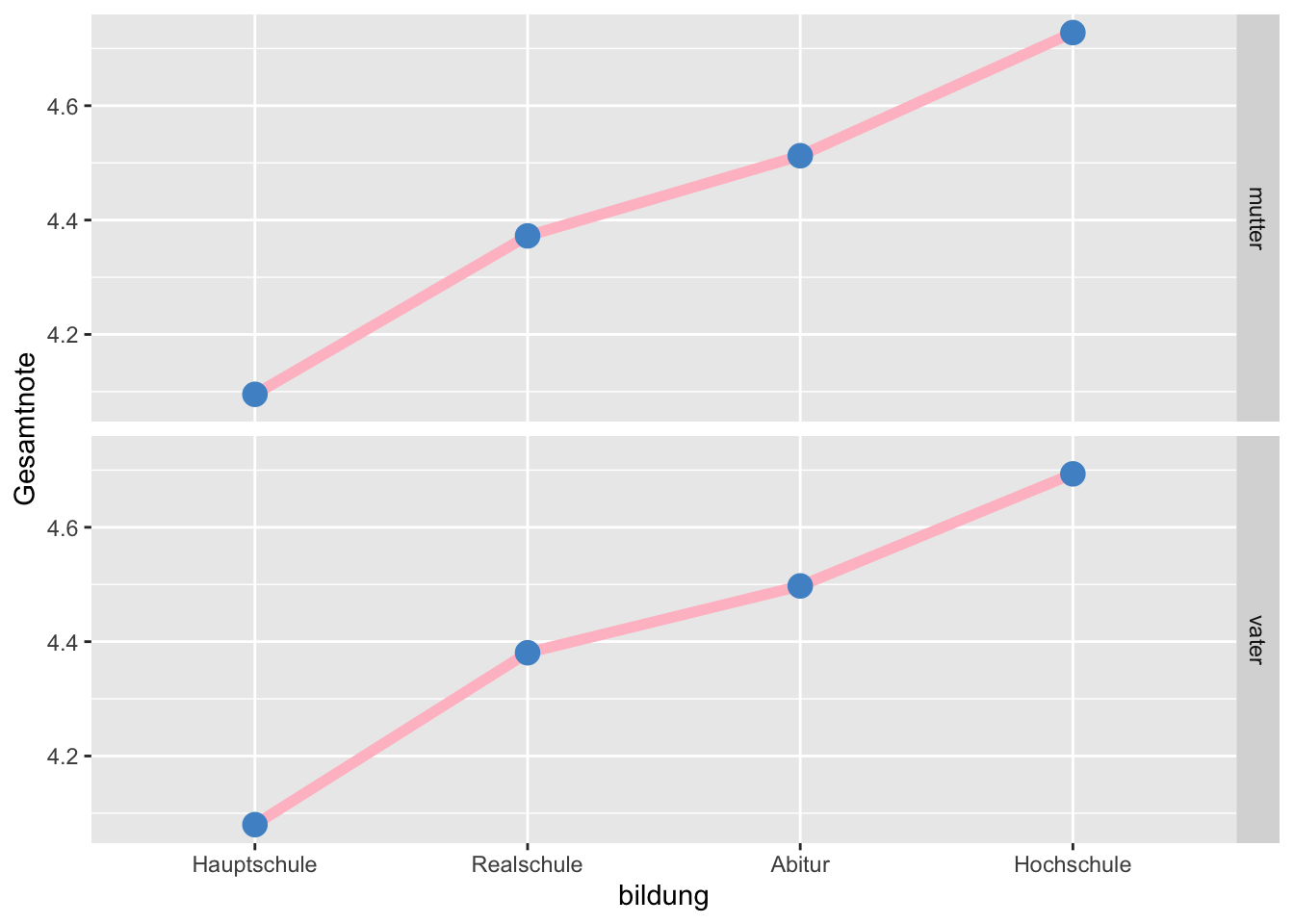
Während in Firma 1 die Arbeitszufriedenheit nach drei Monaten stark abgefallen ist und sich nach sechs Monaten wieder etwas erholt hat, ist sie in Firma 2 über alle drei Messzeitpunkte hoch bzw. steigt sogar etwas an.
Liniendiagramme werden oft benutzt, um den zeitlichen Verlauf einer Variablen darzustellen. Dies bedeutet, dass wir auf der X-Achse die Zeit darstellen, wie in diesem Beispiel. Meistens wird Zeit jedoch als kontinuierliche Variable verwendet und nicht, wie hier, als Faktor.
Wide vs. Long: Bildung der Eltern
Anhand des nächsten Beipiels betrachten wir den Unterschied zwischen dem long und dem wide Format. Wir haben, als wir die gemeinsame Häufigkeitsverteilung der Bildung des Vaters und der Mutter dargestellt haben, bildung_vater und bildung_mutter als separate Variablen verwendet, um sie auf separaten Achsen darzustellen. Wir könnten jedoch auch bildung_vater und bildung_mutter als Stufen eines Messwiederholungsfaktors elternteil (key) zusammenfassen, und die Bildungsniveaus als Messvariable bildung (value), d.h. als key/value Paar. Dies machen wir, wenn wir bildung als Variable auf einer Achse verwenden wollen und elternteil als Gruppierungsvariable.
Dies ist vielleicht nicht ganz einfach zu verstehen, deshalb betrachten wir gleich ein konkretes Beispiel. Wir wollen nun, ähnlich wie oben, die mittlere Schulnote der Jugendlichen für die verschiedenen Bildungsniveaus der Eltern grafisch darstellen. Diesmal machen wir dies für beide Elternteile. Wir wollen jedoch unterschiedliche Linien für Vater und Mutter. Nun ist es wichtig, dass wir einen long Datensatz bilden.
bildung <- beispieldaten |>
# Variablen auswählen
select(Gesamtnote, bildung_vater, bildung_mutter) |>
# Fehlende Werte ausschliessen
drop_na() |>
# wide zu long
pivot_longer(!Gesamtnote, names_to = "elternteil", values_to = "bildung") |>
# Präfix bildung_ bei elternteil-Variable entfernen
mutate(elternteil = str_replace(elternteil, ".*_", "")) |>
# zu Faktoren konvertieren
mutate(
elternteil = factor(elternteil, levels = c("mutter", "vater")),
bildung = factor(bildung, levels = c(
"Hauptschule", "Realschule",
"Abitur", "Hochschule"
))
) |>
# Gruppieren: zuerst Eltern, dann Bildungsniveaus
group_by(elternteil, bildung) |>
# Mittlere Note berechnen
summarize(Gesamtnote = mean(Gesamtnote))`summarise()` has grouped output by 'elternteil'. You can override using the
`.groups` argument.bildung# A tibble: 8 × 3
# Groups: elternteil [2]
elternteil bildung Gesamtnote
<fct> <fct> <dbl>
1 mutter Hauptschule 4.10
2 mutter Realschule 4.37
3 mutter Abitur 4.51
4 mutter Hochschule 4.73
5 vater Hauptschule 4.08
6 vater Realschule 4.38
7 vater Abitur 4.50
8 vater Hochschule 4.69p <- bildung |>
ggplot(aes(
x = bildung,
y = Gesamtnote,
colour = elternteil,
linetype = elternteil,
group = elternteil
))
p + geom_line(linewidth = 2) +
geom_point(size = 4)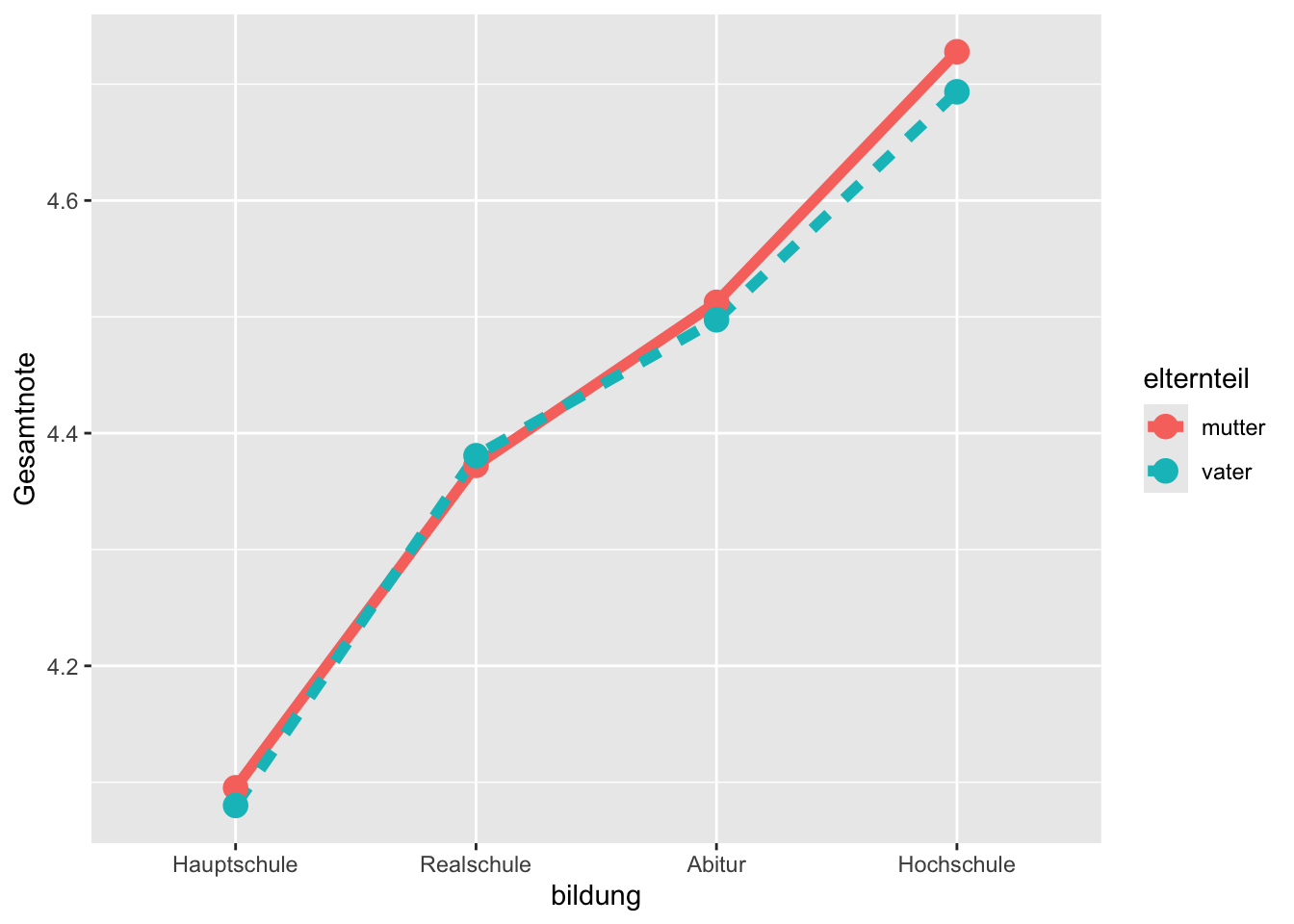
5.5 Facets
Bisher haben wir Gruppierungsvariablen dazu benutzt, um unterschiedliche Farben/Formen/Linien für die Kategorien der Gruppierungsvariable innerhalb eines Plots zu erzeugen. Manchmal ist dies jedoch zu unübersichtlich.
Wollen wir zum Beispiel ein Histogram der Schulnoten erstellen, und zwar für jede Stufe der Bildung der Mutter, dann wäre die Grafik völlig überladen.
p <- beispieldaten |>
select(Gesamtnote, bildung_mutter) |>
drop_na() |>
ggplot(mapping = aes(
x = Gesamtnote,
fill = bildung_mutter
))
p + geom_histogram(
binwidth = 0.8,
position = "dodge"
)
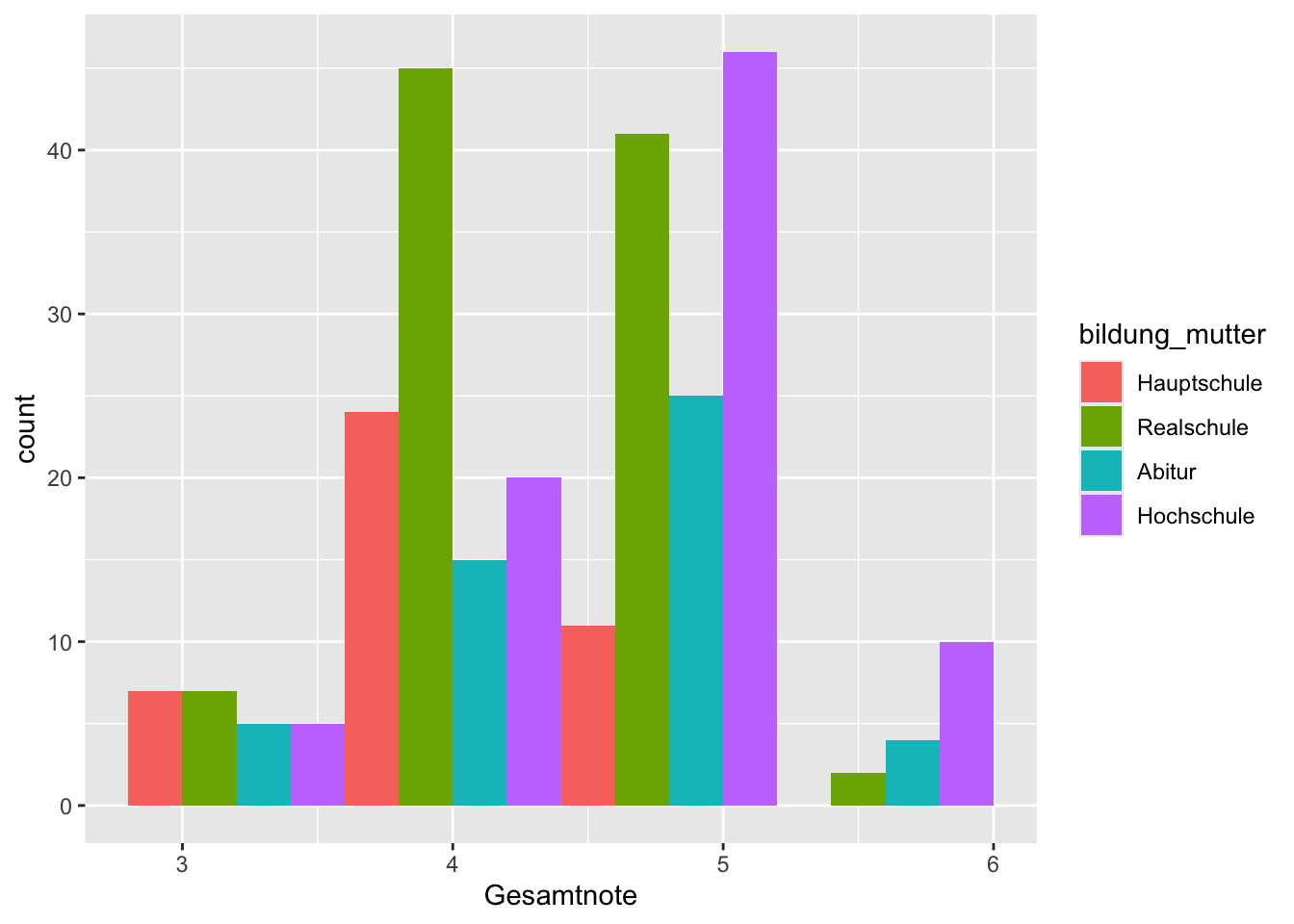
Eine offensichtliche Lösung wäre, die Histogramme für die Bildungsniveaus der Mutter in separaten Grafiken darzustellen.
Genau dies können wir mit den Funktionen facet_wrap() und facet_grid() machen.
Mit facet_wrap() erstellen wir so eine Grafik für jede Kategorie der Gruppierungsvariable:
p <- beispieldaten |>
select(Gesamtnote, bildung_mutter) |>
drop_na() |>
ggplot(mapping = aes(
x = Gesamtnote,
fill = bildung_mutter
)) +
facet_wrap(~bildung_mutter)
p + geom_histogram(binwidth = 0.8)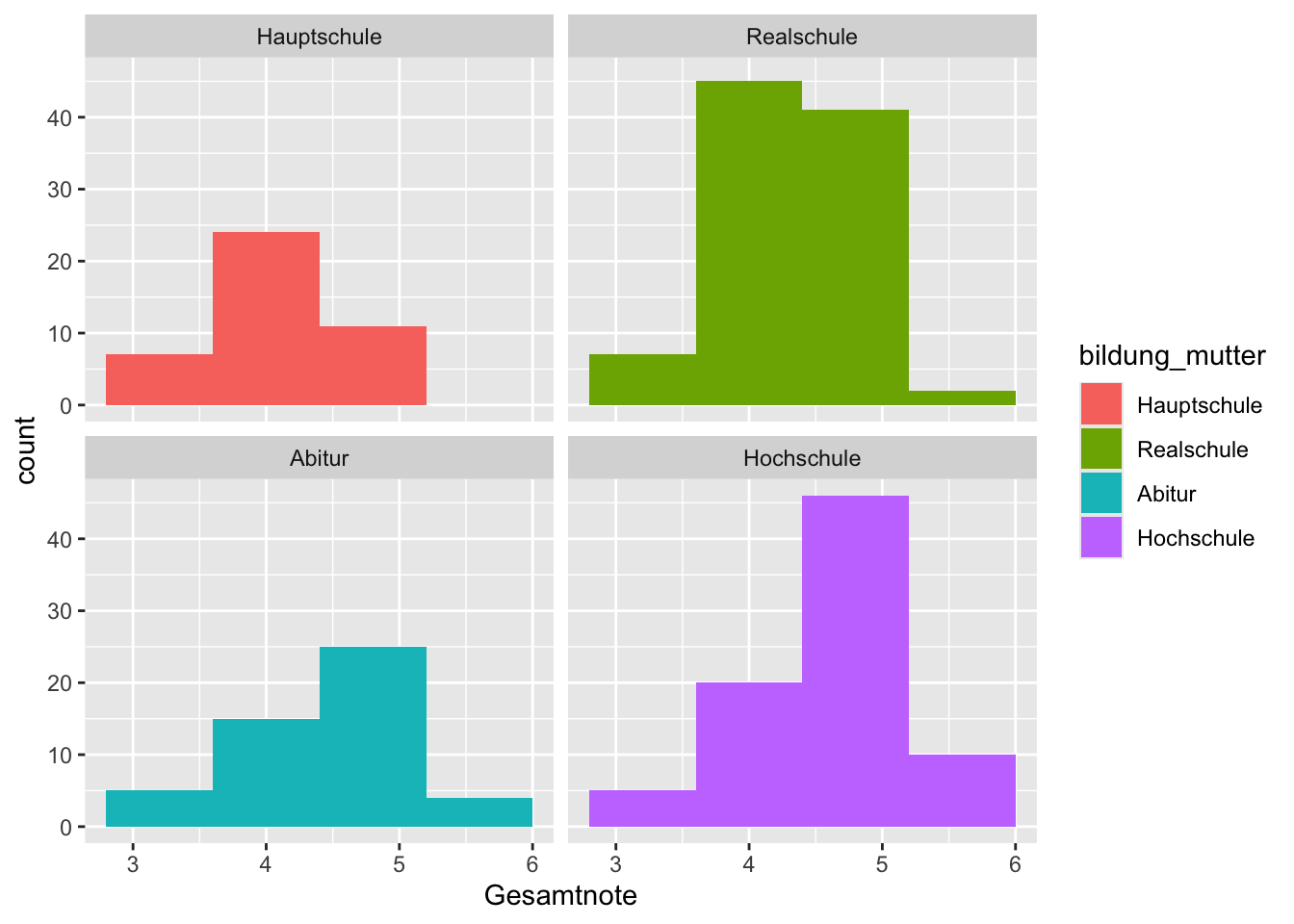
Wenn wir zwei Gruppierungsvariablen haben, können wir mit facet_grid() ein Raster erzeugen.
p <- beispieldaten |>
select(Gesamtnote, bildung_mutter, bildung_vater) |>
drop_na() |>
ggplot(mapping = aes(x = Gesamtnote)) +
facet_grid(bildung_mutter ~ bildung_vater)
p + geom_histogram(
binwidth = 0.8,
fill = "steelblue4"
)
Hier werden die Stufen von bildung_mutter in den Zeilen dargestellt, die Stufen von bildung_vater in den Spalten.
Als zweites Beispiel können wir den Notenschnitt in Abhängigkeit der Bildung der Eltern als Liniendiagram darstellen, und zwar in separaten Plots für Väter und Mütter getrennt. Anhand dieses Beispiels sehen wir, dass wir facet_grid() auch dann verwenden können, wenn wir nur eine Gruppierungsvariable haben, und zwar um die Anzahl Zeilen bzw. Spalten festzulegen.
Wenn wir die Gruppierung in den Zeilen haben wollen, schreiben wir facet_grid(Gruppierungsvariable ~ .), wenn sie in den Spalten wollen, schreiben wir facet_grid(. ~ Gruppierungsvariable). Der Punkt . bedeutet hier, dass wir für die Zeilen/Spalten keine Gruppierungsvariable verwenden.
p <- bildung |>
ggplot(aes(
x = bildung,
y = Gesamtnote,
group = elternteil
))
p + geom_line(linewidth = 2, color = "pink") +
geom_point(size = 4, color = "steelblue3") +
# Stufen von 'elternteil' in die Zeilen
facet_grid(elternteil ~ .)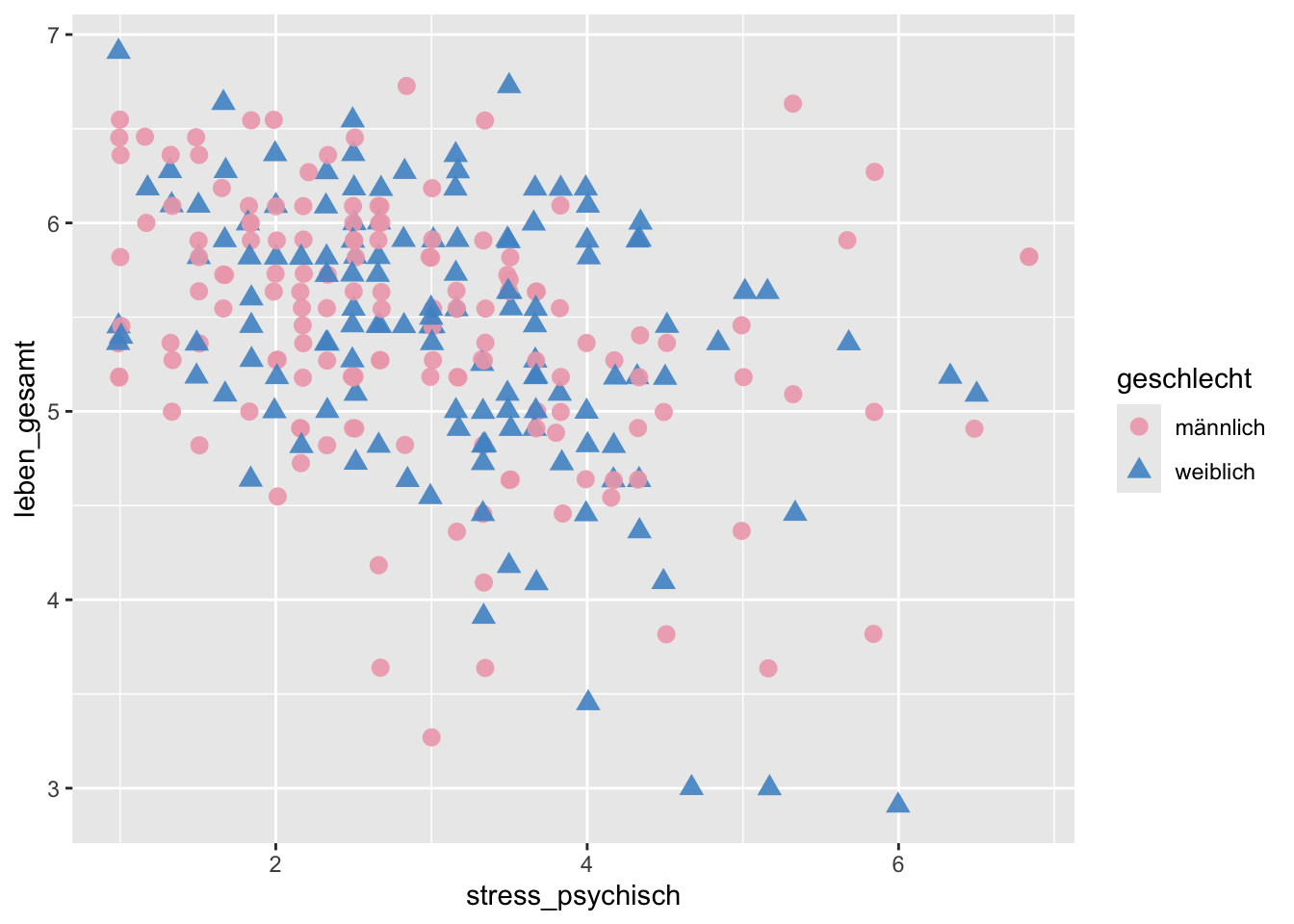
p <- bildung |>
ggplot(aes(
x = bildung,
y = Gesamtnote,
group = elternteil
))
p + geom_line(linewidth = 2, color = "pink") +
geom_point(size = 4, color = "steelblue3") +
# Stufen von 'elternteil' in die Spalten
facet_grid(. ~ elternteil)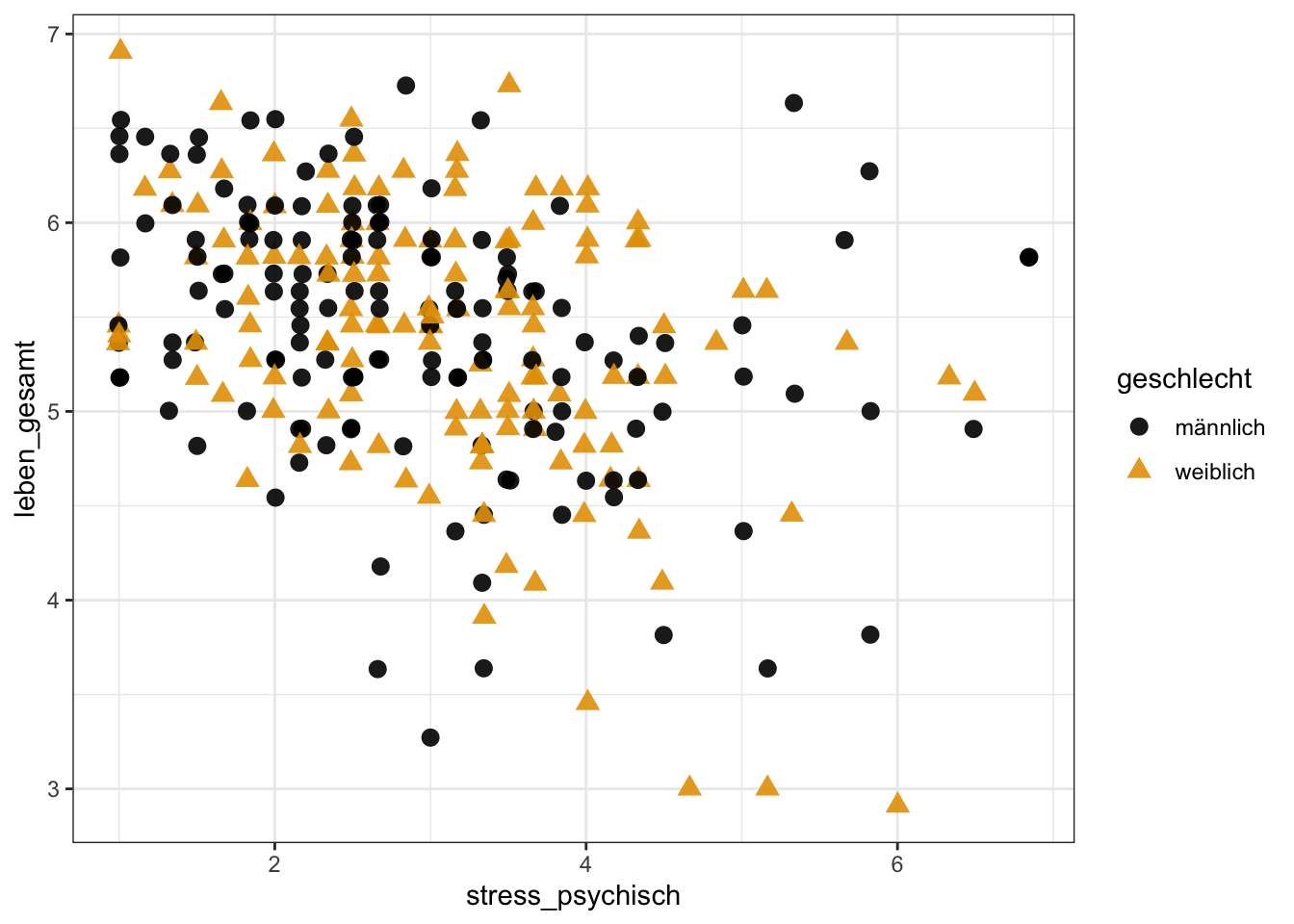
5.6 Farben und Themes
Bisher hat ggplot2 automatisch für uns Farben gewählt, wenn wir Farben für eine Gruppierung verlangt haben. Die Standard Farbpalette ist jedoch für Farbenblinde äusserst schlecht geeignet. Es gibt viele Farbpaletten, welche wir verwenden könnten.
Wir definieren hier jedoch eine eigene, für Farbenblinde geeignete Farbpalette.
palette <- c(
"#000000", "#E69F00",
"#56B4E9", "#009E73",
"#F0E442", "#0072B2",
"#D55E00", "#CC79A7"
)Wir definieren hier also einen Vektor von acht Hex Codes. Folglich dürfte unsere Gruppierungsvariable nicht mehr als acht Kategorien haben.
Die Palette verwenden wir so:
- um Formen auszufüllen, verwenden wir
scale_fill_manual(values = palette)- für Linien und Punkte verwenden wir:
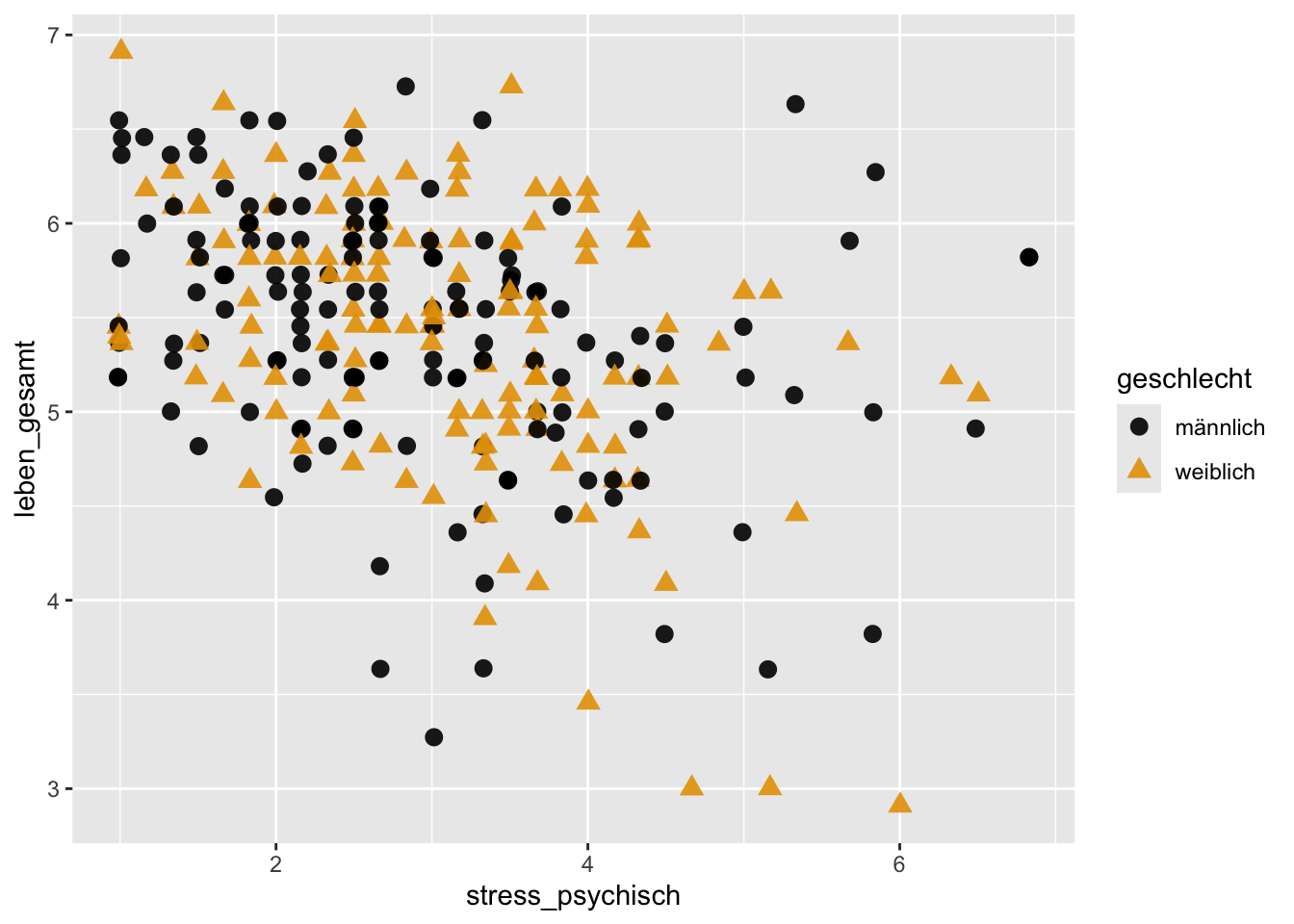
scale_colour_manual(values = palette)Als Beispiel plotten wir nochmals den Zusammenhang zwischen stress_psychisch und leben_gesamt, diesmal mit unserer Farbpalette.
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt, geschlecht) |>
drop_na() |>
ggplot(mapping = aes(
x = stress_psychisch,
y = leben_gesamt,
color = geschlecht,
shape = geschlecht
))
p + geom_jitter(size = 3, alpha = 0.9) +
scale_colour_manual(values = palette)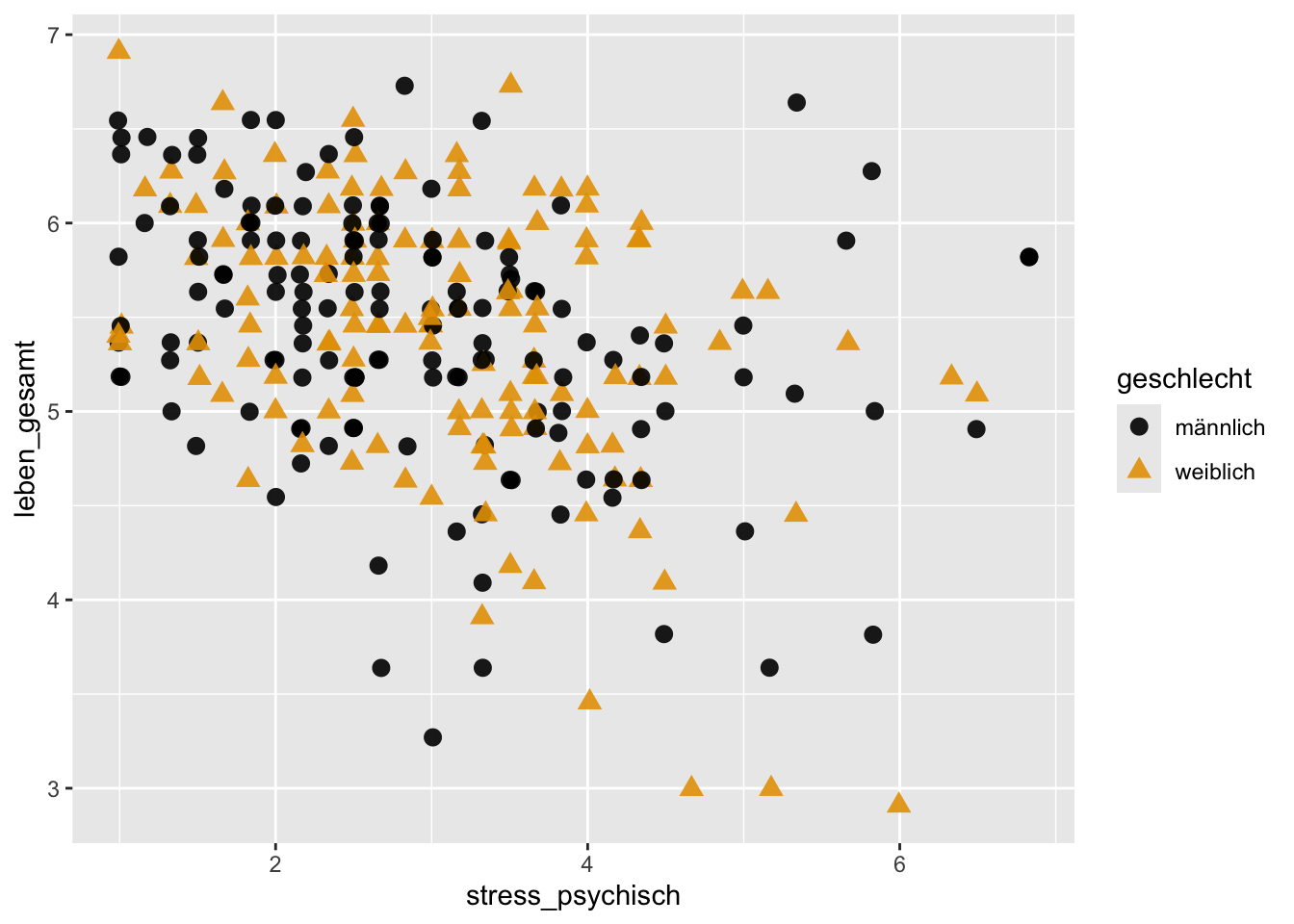
Wir könnten die Farben auch so ‘von Hand’ bestimmen:
p + geom_jitter(size = 3, alpha = 0.9) +
scale_colour_manual(values = c("pink2", "steelblue3"))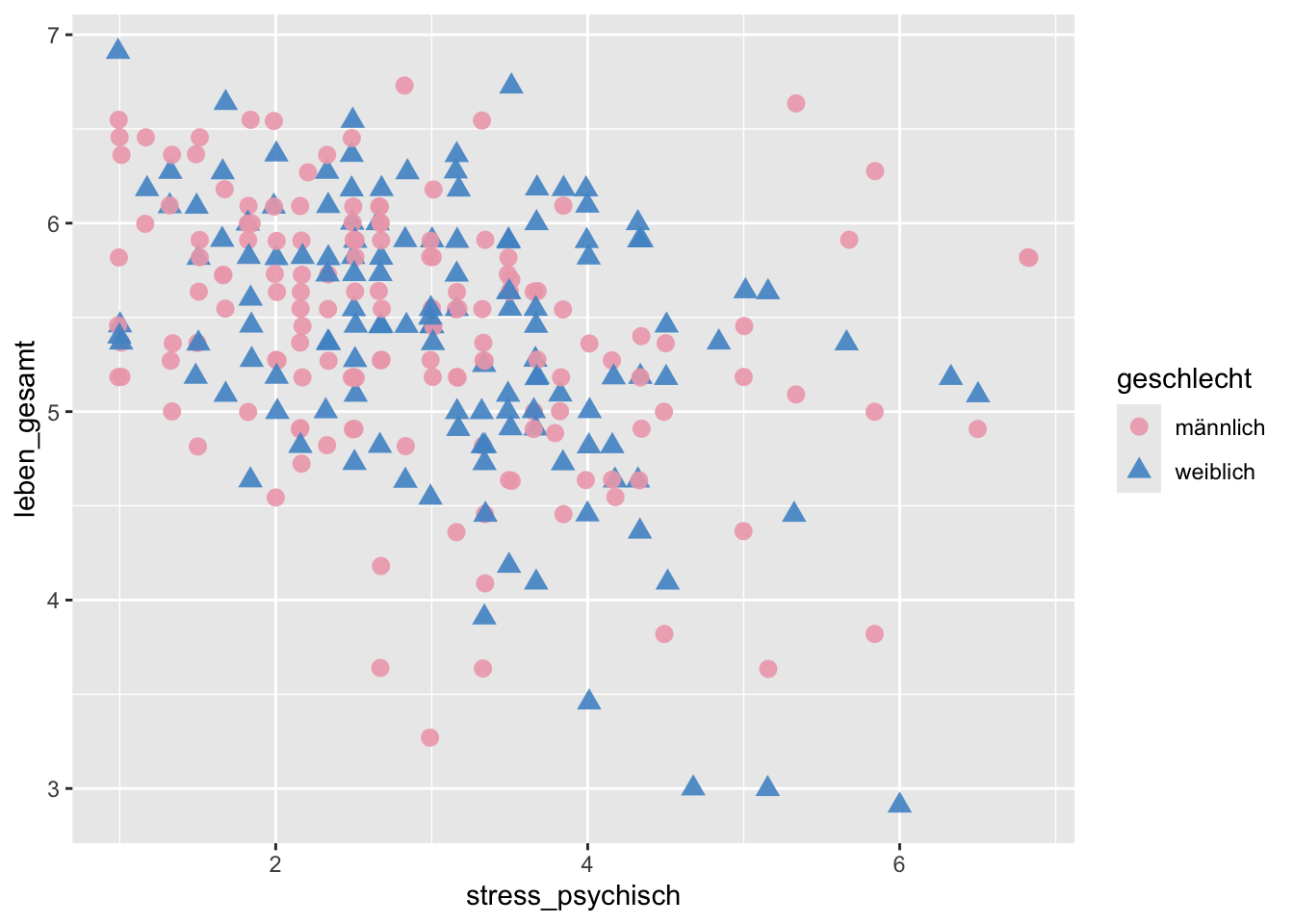
Ein weiterer heikler Punkt ist der graue Hintergrund, den ggplot2 automatisch wählt. Diesen können wir am einfachsten ändern, indem wir ein theme definieren. Es gibt zwei solcher themes, welche einen weissen Hintergrund haben: theme_bw() und theme_classic(). Diese unterscheiden sich darin, dass theme_classic() keine grid lines zeichnet, sondern nur die linke und die untere Achse.
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt, geschlecht) |>
drop_na() |>
ggplot(mapping = aes(
x = stress_psychisch,
y = leben_gesamt,
color = geschlecht,
shape = geschlecht
))
p + geom_jitter(size = 3, alpha = 0.9) +
scale_colour_manual(values = palette) +
theme_bw()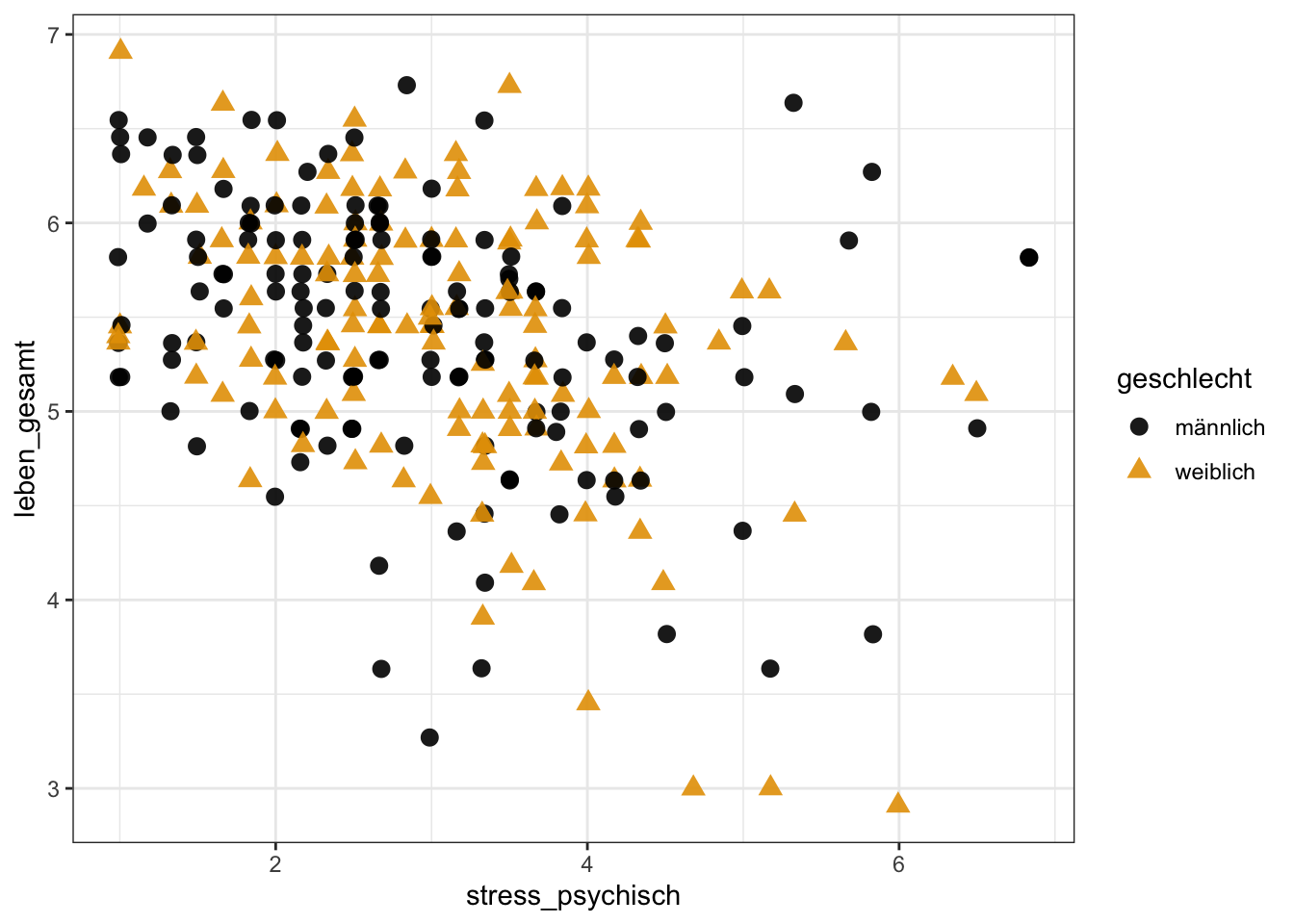
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt, geschlecht) |>
drop_na() |>
ggplot(mapping = aes(
x = stress_psychisch,
y = leben_gesamt,
color = geschlecht,
shape = geschlecht
))
p + geom_jitter(size = 3, alpha = 0.9) +
scale_colour_manual(values = palette) +
theme_classic()
5.7 Beschriftungen
Wir können nun auch noch mit xlab() und ylab() die Beschriftungen der X/Y-Achsen ändern, und mit der Funktion ggtitle() dem Plot einen Titel geben. Mit der Funktion labs() können wir zusätzlich noch den Titel der Legende ändern.
Zuletzt wollen wir auch die Schriftgrösse ändern, da die Standardgrösse oft zu klein erscheint. Dies erreichen wir mit dem Argument base_size = SCHRIFTGRÖSSE) der theme_ Funktionen.
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt, geschlecht) |>
drop_na() |>
ggplot(mapping = aes(
x = stress_psychisch,
y = leben_gesamt,
color = geschlecht,
shape = geschlecht
))
p + geom_jitter(size = 3, alpha = 0.9) +
scale_colour_manual(values = palette) +
theme_classic(base_size = 14) +
ggtitle("Zusammenhang zwischen Stress und Zufriedenheit") +
xlab("Psychischer Stress") +
ylab("Zufriedenheit") +
# "Geschlecht" als Titel der color- und shape-Legende
labs(
color = "Geschlecht",
shape = "Geschlecht"
)
5.8 Grafiken speichern
Wenn wir eine schöne Grafik erstellt haben, wollen wir sie natürlich speichern. Dies können wir mit der Funktion ggsave() machen. Die Funktion nimmt als Argumente den Dateinamen, den Namen des Plot-Objekts und weitere Eigenschaften, wie die gewünschte Höhe und Breite des Plots. Diese können z.B. in “cm” angebenen werden, mit dem Argument units = "cm". Um die Grafik zu speichern, müssen wir unseren fertigen Plot vorher einer Variablen/einem Objekt zuweisen:
p <- beispieldaten |>
select(stress_psychisch, leben_gesamt, geschlecht) |>
drop_na() |>
ggplot(mapping = aes(
x = stress_psychisch,
y = leben_gesamt,
color = geschlecht,
shape = geschlecht
))
# Wir nennen die Grafik 'my_plot'
my_plot <- p + geom_jitter(size = 3, alpha = 0.9) +
scale_colour_manual(values = palette) +
theme_classic(base_size = 14) +
ggtitle("Zusammenhang zwischen Stress und Zufriedenheit") +
xlab("Psychischer Stress") +
ylab("Zufriedenheit") +
labs(
color = "Geschlecht",
shape = "Geschlecht"
)my_plot kann nun gespeichert werden:
ggsave(
filename = "my_plot.png",
plot = my_plot
)Die Grafik kann auch in den Formaten eps, ps, tex, pdf, jpeg, tiff, bmp, svg und wmf gespeichert werden. Dazu muss lediglich die Endung .png ersetzt werden, beispielsweise durch .pdf. Je nach Anwendungszweck lohnt es sich, auf ein anderes Dateiformat zu setzen. Insbesondere wenn die Grafiken vergrössert werden sollen, lohnt es sich, auf ein Vektorgrafikformat wie .svg oder .wmf zu setzen.
5.9 Übungsaufgaben
In diesen Übungsaufgaben wollen wir die Zusammenhänge zwischen den sechs Selbstwirksamkeitsskalen im Datensatz beispieldaten und der psychischen Belastung untersuchen (Aufgaben 1 - 3). Zudem wollen wir Geschlechtsunterschiede in Bezug auf die durchschnittliche Ausprägung von Selbstwirksamkeit und psychischen sowie somatischen Stressymptomen darstellen (Aufgaben 4 und 5).
Aufgabe 1
- Bilden Sie einen Subdatensatz
selbstwirksamkeit_wide, der nur die für die Aufgaben 1 - 3 relevanten Variablen des Datensatzes enthält (ID,geschlecht,stress_psychisch,swk_neueslernen,swk_lernregulation,swk_motivation,swk_durchsetzung,swk_sozialkomp,swk_beziehung) und entfernen Sie fehlende Werte.
- Versuchen Sie zunächst, Zusammenhänge der sechs Selbstwirksamkeitsskalen untereinander zu entdecken, indem Sie diese grafisch darstellen. Erstellen Sie dazu für jedes Variablenpaar einen Scatterplot (Streudiagramm). Insgesamt müssen also 15 Scatterplots erstellt werden.
Tipp
p <- selbstwirksamkeit_wide |>
ggplot()p + geom_jitter(aes(x = swk_neueslernen, y = swk_lernregulation),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_neueslernen, y = swk_motivation),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_neueslernen, y = swk_durchsetzung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_neueslernen, y = swk_sozialkomp),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_neueslernen, y = swk_beziehung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_lernregulation, y = swk_motivation),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_lernregulation, y = swk_durchsetzung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_lernregulation, y = swk_sozialkomp),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_lernregulation, y = swk_beziehung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_motivation, y = swk_durchsetzung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_motivation, y = swk_sozialkomp),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_motivation, y = swk_beziehung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_durchsetzung, y = swk_sozialkomp),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_durchsetzung, y = swk_beziehung),
alpha = 0.6, size = 2)
p + geom_jitter(aes(x = swk_sozialkomp, y = swk_beziehung),
alpha = 0.6, size = 2)
Hinweis
Einfacher geht das mit der Funktion ggpairs() aus dem Package GGally, das wir zunächst installieren müssen:
install.packages("GGally")library(GGally)
selbstwirksamkeit_wide |>
select(starts_with("swk_")) |>
ggpairs()
Hier bekommen wir neben den insgesamt 15 Scatterplots (untere Dreiecksmatrix) auch noch einen Density-Plot pro Variable in der Diagonalen ausgegeben, sowie die bivariaten Pearson-Korrelationen in der oberen Dreiecksmatrix (inkl. Signifikanztest, erkennbar an der Sternchen-Kennzeichnung: *** bedeutet p < 0.001).
Aufgabe 2
Stellen Sie nun auch die Zusammenhänge zwischen den sechs Selbstwirksamkeitsskalen und der psychischen Symptomatik jeweils mit einem Scatterplot dar. Nutzen Sie dabei geschlecht als Gruppierungsvariable, und zwar wie oben für das color- und für das shape-Argument. Insgesamt müssen dafür sechs Scatterplots erstellt werden.
Tipp
p <- selbstwirksamkeit_wide |>
ggplot(mapping = aes(
color = geschlecht,
shape = geschlecht
))
p + geom_jitter(aes(x = swk_neueslernen, y = stress_psychisch),
alpha = 0.8, size = 2) +
scale_color_manual(values = c("#000000", "#E69F00"))
p + geom_jitter(aes(x = swk_lernregulation, y = stress_psychisch),
alpha = 0.8, size = 2) +
scale_color_manual(values = c("#000000", "#E69F00"))
p + geom_jitter(aes(x = swk_motivation, y = stress_psychisch),
alpha = 0.8, size = 2) +
scale_color_manual(values = c("#000000", "#E69F00"))
p + geom_jitter(aes(x = swk_durchsetzung, y = stress_psychisch),
alpha = 0.8, size = 2) +
scale_color_manual(values = c("#000000", "#E69F00"))
p + geom_jitter(aes(x = swk_sozialkomp, y = stress_psychisch),
alpha = 0.8, size = 2) +
scale_color_manual(values = c("#000000", "#E69F00"))
p + geom_jitter(aes(x = swk_beziehung, y = stress_psychisch),
alpha = 0.8, size = 2) +
scale_color_manual(values = c("#000000", "#E69F00"))
Tendenziell sieht es so aus, dass höhere Werte in der Selbstwirksamkeit mit niedrigerem psychischen Stress einhergehen (bei beiden Geschlechtern). Es wäre noch interessant, diese Beobachtung über die entsprechenden bivariaten Pearson-Korrelationskoeffizienten zu bestätigen.
Um nur die Korrelationen der sechs Selbstwirksamkeitsskalen mit der Variablen stress_psychisch zu erhalten (und nicht die Korrelationen aller Variablen untereinander), können wir die Funktion cor(x, y) nutzen, wobei x in diesem Fall ein Dataframe mit den sechs swk_-Variablen sein muss und y ein Dataframe, der nur die Variable stress_psychisch enthält. Um um die Korrelationen getrennt für männliche und weibliche Jugendliche zu erhalten, müssen wir diese Dataframes getrennt nach Geschlecht erstellen:
# Dataframes für Korrelationen für männliche Jugendliche
selbstwirksamkeit_maennlich <- selbstwirksamkeit_wide |>
filter(geschlecht == "männlich") |>
select(starts_with("swk"))
stress_psychisch_maennlich <- selbstwirksamkeit_wide |>
filter(geschlecht == "männlich") |>
select(stress_psychisch)
# Dataframes für Korrelationen für weibliche Jugendliche
selbstwirksamkeit_weiblich <- selbstwirksamkeit_wide |>
filter(geschlecht == "weiblich") |>
select(starts_with("swk"))
stress_psychisch_weiblich <- selbstwirksamkeit_wide |>
filter(geschlecht == "weiblich") |>
select(stress_psychisch) # Korrelationen berechnen
cor(x = selbstwirksamkeit_maennlich, y = stress_psychisch_maennlich) stress_psychisch
swk_neueslernen -0.05253377
swk_lernregulation -0.12120519
swk_motivation -0.10186382
swk_durchsetzung -0.13215266
swk_sozialkomp -0.12918169
swk_beziehung -0.11275072cor(x = selbstwirksamkeit_weiblich, y = stress_psychisch_weiblich) stress_psychisch
swk_neueslernen -0.053960724
swk_lernregulation -0.151537381
swk_motivation -0.006650242
swk_durchsetzung -0.258573830
swk_sozialkomp -0.301637007
swk_beziehung -0.266703463Während die Korrelationen der drei akademischen Selbstwirksamkeitsbereiche swk_neueslernen, swk_lernregulation und swk_motivation mit stress_psychisch sehr schwach sind und sich kaum zwischen den Geschlechtern unterscheiden, sind die Korrelationen der drei sozialen Selbstwirksamkeitsbereiche swk_durchsetzung, swk_sozialkomp und swk_beziehung mit stress_psychisch und vor allem bei den weiblichen Jugendlichen etwas stärker negativ. Insbesondere bei Mädchen gehen hohe soziale Selbstwirksamkeitsüberzeugungen daher (rein deskriptiv, auf Signifikanztests verzichten wir hier) mit niedrigeren Stresssymptomen einher.
Aufgabe 3
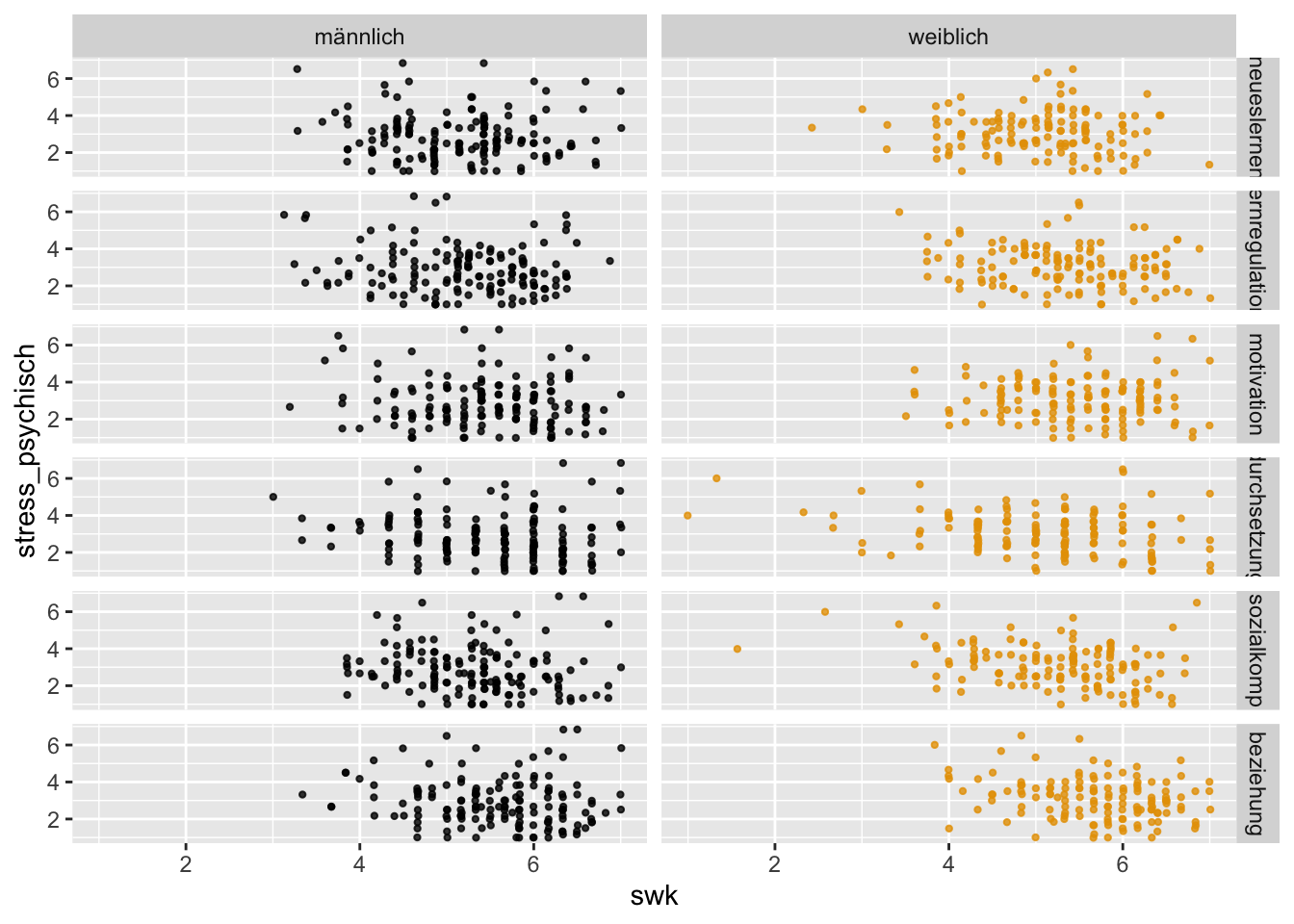
Nun sollen dieselben Streudiagramme wie oben erstellt werden, diesmal aber so, dass für jeden Selbstwirksamkeitsbereich ein eigener Teilplot erstellt wird. Ausserdem sollen jetzt für Jungen und Mädchen jeweils getrennte Plots erstellt werden. Das ist mithilfe der Funktion facet_grid(bereich ~ geschlecht) möglich.
Dafür wird ein (messwiederholter) Faktor bereich benötigt, der anzeigt, zu welchem Selbstwirksamkeitsbereich ein bestimmter Wert einer einzigen Variable swk gehört.
- Führen Sie eine entsprechende wide-to-long Transformation des Datensatzes
selbstwirksamkeit_widedurch (Ergebnis:selbstwirksamkeit_long).
- Jetzt kann geplottet werden. Um es noch ein bisschen schöner zu machen, wollen wir unterschiedliche Farben für die Plots von Jungen und Mädchen verwenden:
Tipp
p <- selbstwirksamkeit_long |>
ggplot(aes(x = swk, y = stress_psychisch)) +
facet_grid(bereich ~ geschlecht)
p +
geom_jitter(alpha = 0.8, size = 0.8, aes(color = geschlecht)) +
scale_color_manual(values = c("#000000", "#E69F00"), guide = "none") 
# guide = "none" entfernt die in diesem Fall nicht benötigte Legende Aufgabe 4
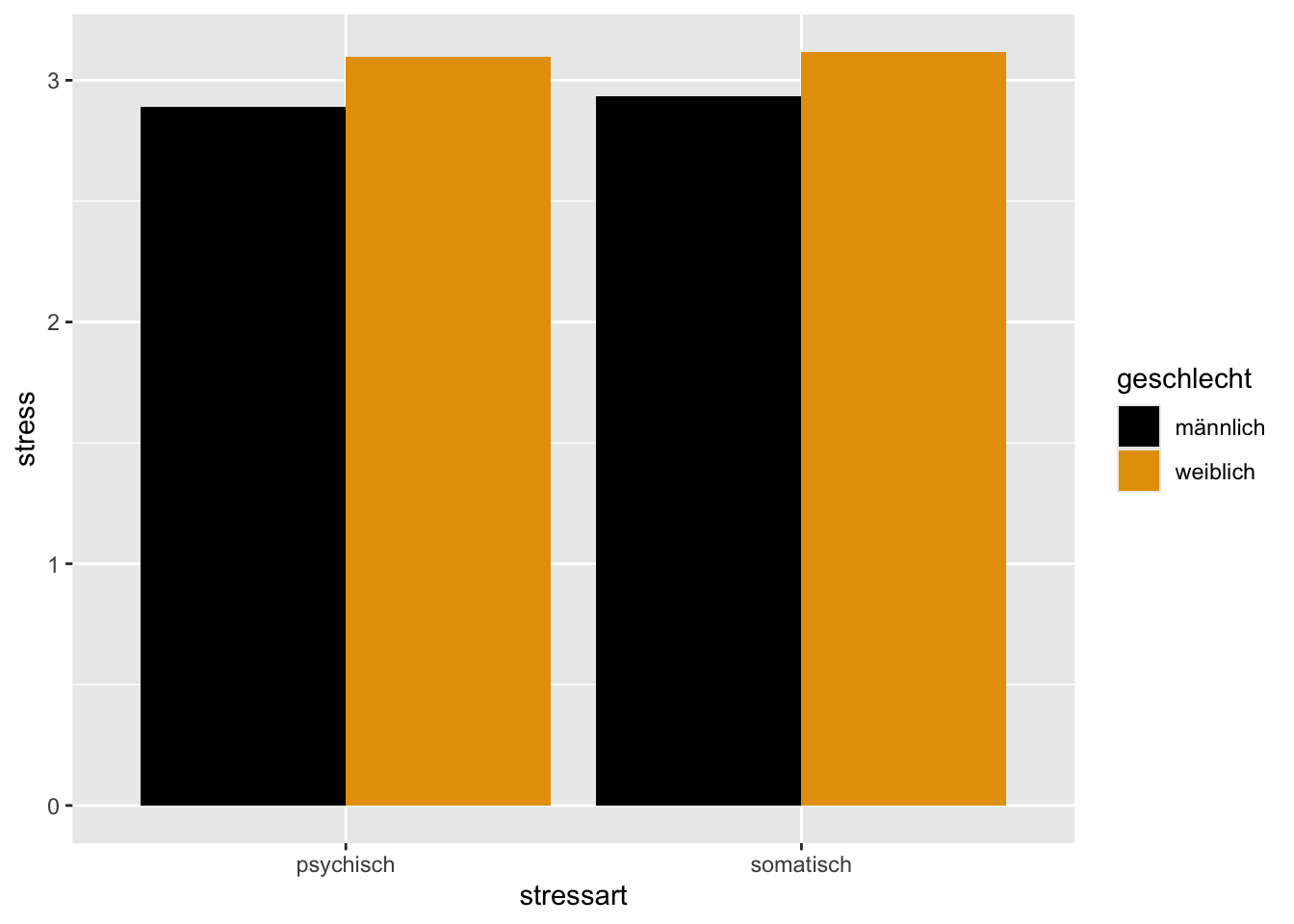
Im einführenden Beispiel ganz am Anfang dieses Kapitels haben wir die Verteilung von stress_psychisch zwischen Jungen und Mädchen verglichen, u.a. mit einem Box-Plot (geom_boxplot) und einem Violin-Plot (geom_violin). Oft will man aber nicht die ganze Verteilung einer Variablen vergleichend darstellen, sondern nur die Mittelwerte. Um es noch etwas interessanter zu machen, wollen wir jetzt nicht nur die Mittelwerte von stress_psychisch zwischen den Geschlechtern vergleichend darstellen, sondern auch diejenigen von stress_somatisch (Skala zu somatischen Stresssymptomen wie z.B. Kopfschmerzen und Schlafstörungen).
Führen Sie folgende Schritte durch:
- Bilden Sie aus
beispieldateneinen Subdatensatz, der nur die VariablenID,geschlecht,stress_psychischundstress_somatischenthält und entfernen Sie fehlende Werte. Nennen Sie den resultierenden Dataframestress_wide.
- Führen Sie wie in Aufgabe 3 eine wide-to-long Transformation durch und bilden Sie damit einen Dataframe
stress_longmit einem messwiederholten Faktorstressart(psychisch vs. somatisch) und der (Outcome-)Variablestress(die die Ausprägungen der Variablenstress_psychischundstress_somatischenthält). Berechnen Sie anschliessend mittelsgroup_by()undsummarize()die Mittelwerte vonstressgetrennt nachstressartundgeschlechtund speichern Sie diese in einem Dataframestress_meansab.
- Plotten Sie diese Mittelwerte mittels eines Balkendiagramms (Bar-Plot:
geom_bar()) mit den beiden Stressarten auf der X-Achse, den Stress-Werten auf der Y-Achse und mitgeschlechtals (farbliche) Gruppierungsvariable. Plotten Sie diesmal direkt (ohne vorherige Definition eines Plotobjekts).
Tipp
stress_means |>
ggplot(aes(x = stressart, y = stress, fill = geschlecht)) +
geom_bar(stat = "identity", position = "dodge") +
scale_fill_manual(values = c("#000000", "#E69F00"))
Es fällt auf, dass Y-Achse hier bei 0 beginnt und bei knapp über 3 endet (ca. dort wo die Balken enden). Da der Wert 0 auf der Stress-Skala von 1 bis 7 gar nicht existiert, wäre es sinnvoll, die Y-Achse erst beim Wert 1 beginnen zu lassen, ausserdem könnte man den ganzen möglichen Wertebereich der Stressskala auf der Y-Achse anzeigen lassen, um einen zutreffenderen Gesamteindruck von der Höhe der Stresssymptome und der Geschlechtsunterschiede zu erhalten. Das ist möglich mit der bisher nicht besprochenen ggplot2-Funktion coord_cartesian(), wie im Folgenden gezeigt wird.
Hinweis
stress_means |>
ggplot(aes(x = stressart, y = stress, fill = geschlecht)) +
geom_bar(stat = "identity", position = "dodge") +
scale_fill_manual(values = c("#000000", "#E69F00")) +
coord_cartesian(ylim = c(1, 7), expand = FALSE)
In coord_cartesian() bestimmt das Argument ylim = c(1, 7) Anfang und Ende der Y-Achse, und expand = FALSE macht, dass die Achse genau beim Wert 1 beginnt und genau beim Wert 7 endet (und nicht leicht darüber hinaus erweitert wird wie mit expand = TRUE).
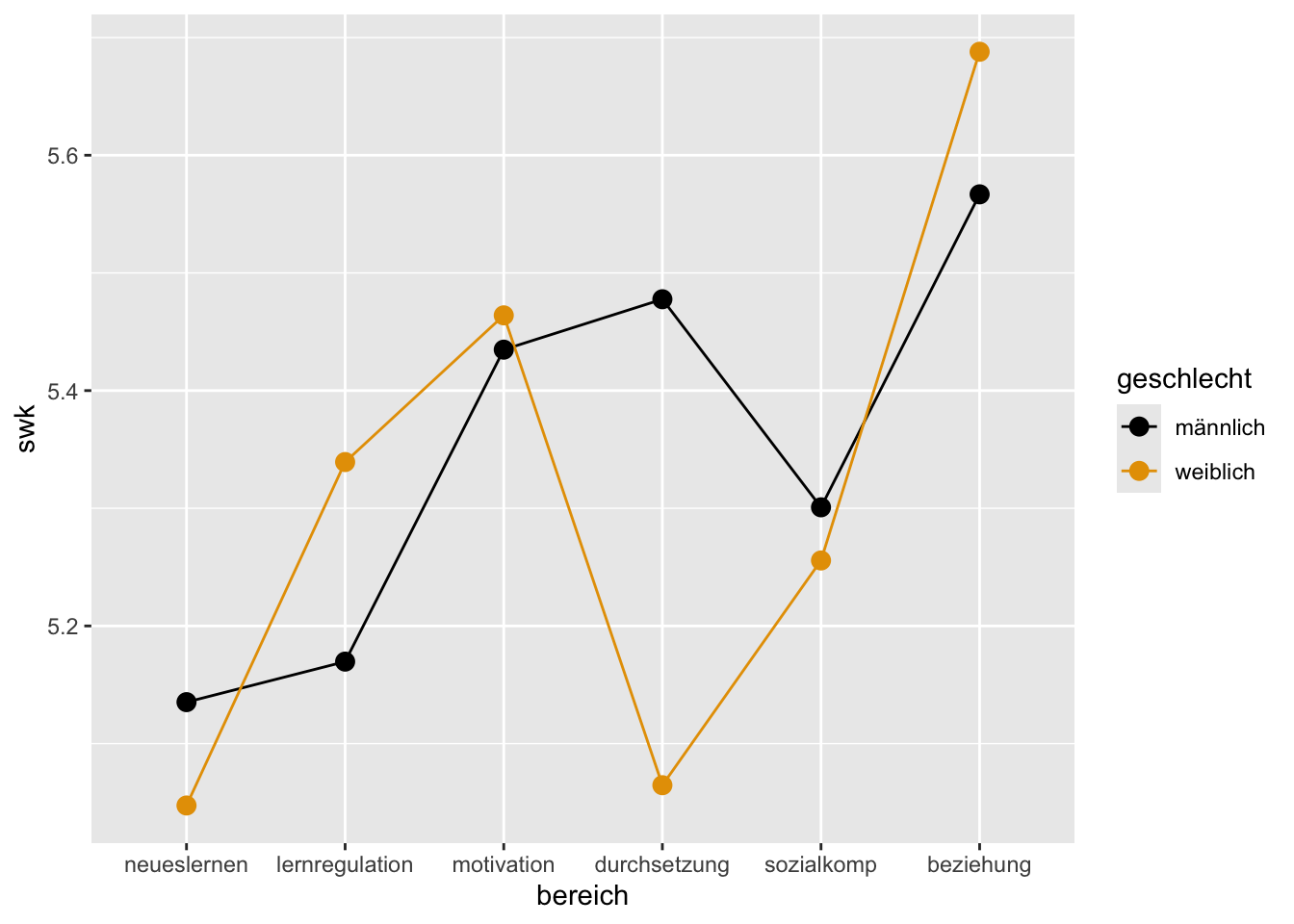
Aufgabe 5
Jetzt sollen auch noch für die sechs Selbstwirksamkeitsskalen Mittelwertsvergleiche zwischen Jungen und Mädchen geplottet werden. Gehen Sie dabei genauso wie in Aufgabe 4 vor, aber benutzen Sie statt eines Bar-Plots ein Liniendiagramm mit zusätzlichen Punkten.
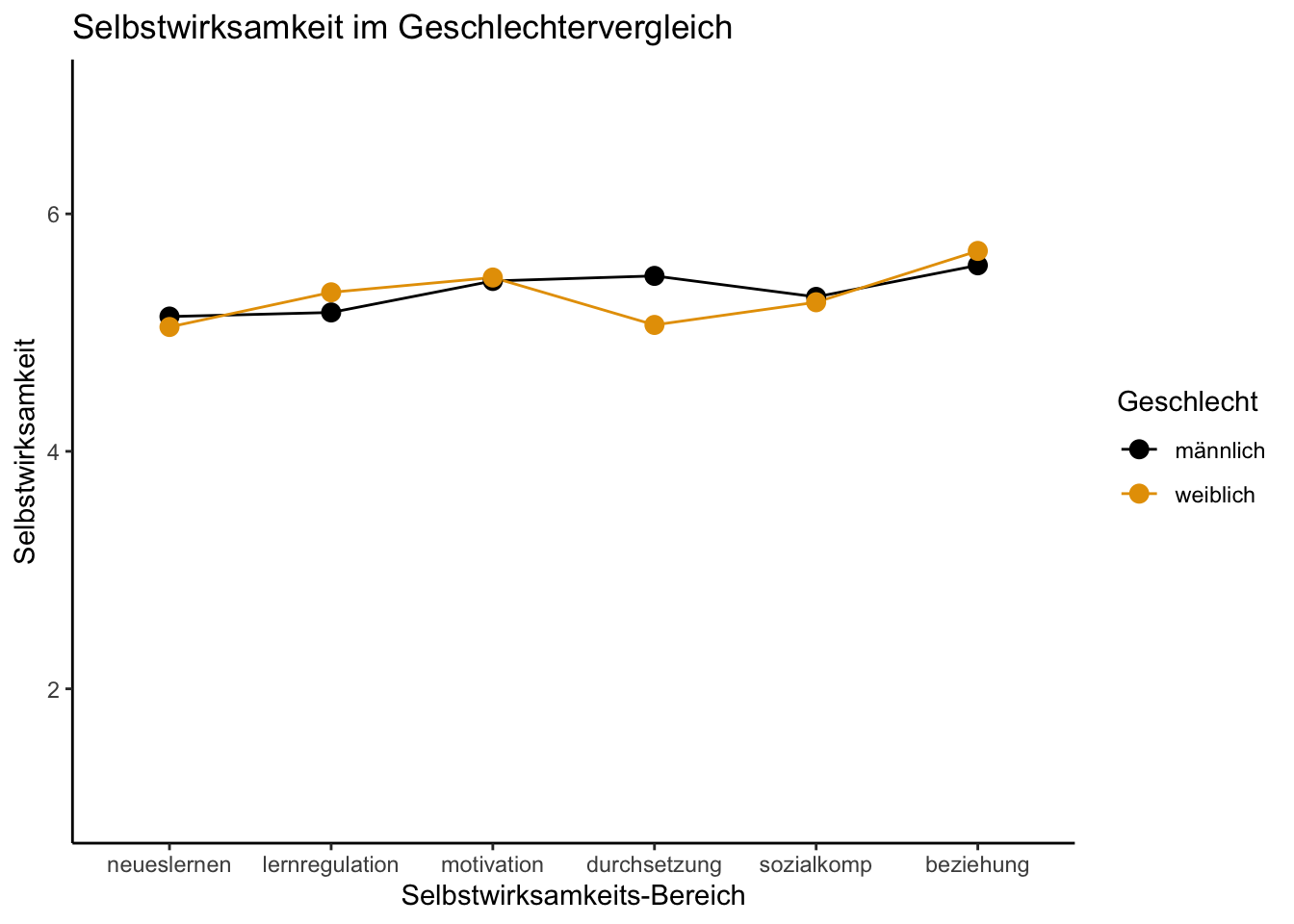
Benutzen Sie den in Aufgabe 3 gebildeten Datensatz selbstwirksamkeit_long zunächst, um die zu plottenden Mittelwerte zu berechnen.
Zum Abschluss soll der Plot noch (weiter) verschönert werden: er soll einen weissen Hintergrund bekommen sowie einen Titel und bessere (bzw. korrektere) Achsen- und Legendenbeschriftungen.
Plotten Sie wieder direkt (ohne vorherige Definition eines Plotobjekts).
Tipp
swk_means <- selbstwirksamkeit_long |>
group_by(bereich, geschlecht) |>
summarize(swk = mean(swk))
swk_means |>
ggplot(aes(x = bereich, y = swk, color = geschlecht)) +
geom_line(aes(group = geschlecht)) +
geom_point(size = 3) +
scale_color_manual(values = c("#000000", "#E69F00")) 
Ohne die coord_cartesian()-Funktion wird hier nur derjenige Auschnitt der swk-Skala dargestellt, in dem sich die zu plottenden Mittelwerte befinden (diese liegen zwischen 5.05 und 5.69, s.o.). Dadurch wirkt es hier so, als gäbe es relativ grosse Geschlechtsunterschiede in der Selbstwirksamkeit, je nach Bereich in unterschiedliche Richtungen. Tatsächlich handelt es sich relativ zur Gesamtskala (1 bis 7) aber grösstenteils um sehr geringe Unterschiede.
Daher plotten wir noch einmal und geben jetzt mit Hilfe von coord_cartesian() an, dass die Y-Achse von 1 bis 7 gehen soll. Diesmal wählen wir expand = TRUE (default), damit wir links und rechts ein bisschen Platz für die Darstellung der Punkte bekommen (mit expand = FALSE würden die Punkte des ersten Bereichs neueslernen und die des letzten Bereichs beziehung nicht vollständig geplottet).
Ausserdem jetzt mit den Achsenbeschriftungen etc.:
swk_means |>
ggplot(aes(x = bereich, y = swk, color = geschlecht)) +
geom_line(aes(group = geschlecht)) +
geom_point(size = 3) +
scale_color_manual(values = c("#000000", "#E69F00")) +
coord_cartesian(ylim = c(1, 7), expand = TRUE) +
theme_classic() +
ggtitle("Selbstwirksamkeit im Geschlechtervergleich") +
xlab("Selbstwirksamkeits-Bereich") +
ylab("Selbstwirksamkeit") +
labs(color = "Geschlecht")
In dieser Darstellung kann man jetzt gut erkennen, dass einzig im Bereich der Durchsetzungsfähigkeit (durchsetzung) ein etwas grösserer Geschlechtsunterschied besteht (Jungen geben dort eine höhere Selbstwirksamkeitsüberzeugung an als Mädchen). Alle anderen Unterschiede sind sehr gering.