9 Mean Comparisons
9.1 One-sample t-test
Sometimes we want to compare a sample mean with a known population mean \((\mu_0)\) or some other fixed comparison value. For example, we would like to know whether the reported support by friends unt_freunde differs significantly from the midpoint of the 7-point-Likert scale \((\mu_0=4)\).
The required function is t.test(). For the one-sample t-test, we only need the following arguments (incl. default values): alternative = c("two.sided", "less", "greater"), mu = 0, and conf.level = .95.
load(file = "data/adolescents.Rdata")
TTest <- adolescents$unt_freunde %>%
t.test(alternative = 'two.sided',
mu = 4,
conf.level = .95)
TTest
#>
#> One Sample t-test
#>
#> data: .
#> t = 33.781, df = 284, p-value < 2.2e-16
#> alternative hypothesis: true mean is not equal to 4
#> 95 percent confidence interval:
#> 5.815396 6.040043
#> sample estimates:
#> mean of x
#> 5.927719The output of the t.test() function is a list of the object class “htest” (hypothesis test).
typeof(TTest)
#> [1] "list"
attributes(TTest)
#> $names
#> [1] "statistic" "parameter" "p.value" "conf.int" "estimate"
#> [6] "null.value" "stderr" "alternative" "method" "data.name"
#>
#> $class
#> [1] "htest"The elements of this list can be selected individually. The (estimated) means can be obtained with:
The \(p\)-value is returned with:
Degrees of freedom:
Confidence Interval:
The result shows that the sample mean (5.93) is signficantly different from the midpoint of the scale (=4) ($p=$0).
By default we obtained a two-sided test for \((H_1:\mu\neq\mu_0)\). One-sided tests are obtained with alternative = "greater" \((H_1:\mu>\mu_0\) or alternative = "less" \((H_1:\mu<\mu_0)\).
One-sample t-test with jmv:
library(jmv)
ttestOneS(
data = adolescents,
vars = "unt_freunde",
wilcoxon = FALSE, # if TRUE -> Nonparametric Wilcoxon Rank Sum Test
testValue = 4, # a number specifying the value of the null hypothesis (mu0)
hypothesis = "dt", # 'dt' (different to - default), 'gt' (greater than),
# 'lt' (less than)
norm = TRUE, # test for normality of the DV (Shapiro-Wilk test)
meanDiff = TRUE, # display estimated mean difference
effectSize = FALSE, # Cohen's d
ci = TRUE, # confidence interval of the mean difference
ciWidth = 99, # CI width default: 95%
desc = TRUE) # descriptive statistics
#>
#> ONE SAMPLE T-TEST
#>
#> One Sample T-Test
#> ─────────────────────────────────────────────────────────────────────────────────────────────────
#> statistic df p Mean difference Lower Upper
#> ─────────────────────────────────────────────────────────────────────────────────────────────────
#> unt_freunde Student's t 33.8 284 < .001 1.93 1.78 2.08
#> ─────────────────────────────────────────────────────────────────────────────────────────────────
#> Note. Hₐ population mean ≠ 4
#>
#>
#> Test of Normality (Shapiro-Wilk)
#> ──────────────────────────────────
#> W p
#> ──────────────────────────────────
#> unt_freunde 0.892 < .001
#> ──────────────────────────────────
#> Note. A low p-value suggests
#> a violation of the
#> assumption of normality
#>
#>
#> Descriptives
#> ───────────────────────────────────────────────────────────
#> N Mean Median SD SE
#> ───────────────────────────────────────────────────────────
#> unt_freunde 285 5.93 6.00 0.963 0.0571
#> ───────────────────────────────────────────────────────────9.2 Comparison of two sample means
9.2.1 Two independent samples
Independent samples t-test
t.test() works also For the independent samples t-test. In this case, the test variable and the factor are specified in the formula notation typical for R: variable ~ factor (\(\rightarrow\) “variable by factor” = “test variable is predicted by factor” = “test the DV mean difference between the two levels of the factor”).
Furthermore, it has to be indicated whether the assumption of equal variances holds in the two groups: for var.equal = FALSE (default), the Welch Two Sample t-test (heteroscedasticity corrected t-test) is applied, for var.equal = TRUE the standard Student’s t-test.
Again, different alternative hypotheses can be specified. For directional hypotheses (one-sided tests), the order of the factor levels has to be considered. For example, if we assume that girls will report a higher support received from friends than boys and the factor geschlecht has as its first level maennlich, the correct alternative hypothesis is \(H_1:\mu_{boys} < \mu_{girls}\). The required argument is alternative = "less" since formally the mean difference of the two groups is compared to 0, thus in our case \(H_1:\mu_{boy}-\mu_{girl}<0\).
Let’s assume first that the population variances of unt_freunde are equal for boys and girls and carry out the “normal” t-test:
levels(adolescents$geschlecht)
#> [1] "männlich" "weiblich"
t.test(unt_freunde ~ geschlecht, alternative = "less",
conf.level = .95,
var.equal = TRUE,
data = adolescents)
#>
#> Two Sample t-test
#>
#> data: unt_freunde by geschlecht
#> t = -6.9351, df = 283, p-value = 1.379e-11
#> alternative hypothesis: true difference in means is less than 0
#> 95 percent confidence interval:
#> -Inf -0.5598577
#> sample estimates:
#> mean in group männlich mean in group weiblich
#> 5.584868 6.319549To check the assumption of homoscedasticity, we perform the Levene test using the function leveneTest() from the car package. In addition to the test variable and the factor we have to specify whether mean or median should be used for the deviations: for center = mean the (actual) Levene test is performed, for center = median (default) the Brown-Forsythe test, a more robust variant of the Levene test is performed.
library(car)
leveneTest(adolescents$unt_freunde, adolescents$geschlecht,
center = median)
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 1 11.987 0.0006185 ***
#> 283
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Since the Levene test is significant, the null hypothesis of homoscedasticity is rejected. Thus, we have to perform the t-test again as a Welch test.
t.test(unt_freunde ~ geschlecht, alternative = "less",
conf.level = .95, var.equal = FALSE,
data = adolescents)
#>
#> Welch Two Sample t-test
#>
#> data: unt_freunde by geschlecht
#> t = -7.0735, df = 275.37, p-value = 6.251e-12
#> alternative hypothesis: true difference in means is less than 0
#> 95 percent confidence interval:
#> -Inf -0.5632619
#> sample estimates:
#> mean in group männlich mean in group weiblich
#> 5.584868 6.319549Wilcoxon Rank Sum test (Mann-Whitney U test)
A nonparametric alternative to the independent sample t-test is the Wilcoxon rank sum test. It tests whether the average sum of the ranks (and thus the medians) of the two samples differ significantly from each other. Nonparametric tests are often used with small samples when distributional assumptions are not met.
As an example, let’s compare the medians of a small subsample of boys and girls (first 35 rows of the data set) with respect to the variable unt_freunde. The function is wilcox.test() and its structure is similar to t.test(). There are two additional arguments: exact = TRUE performs an exact test, but it works only when there are no ties present (no two values are the same across both groups); the second argument is correct = FALSE for an uncorrected (orginal) Wilcoxon test (otherwise a test with continuity correction is performed).
# Create subsample
adolescents_small <- adolescents[1:35,] %>%
select(ID, geschlecht, unt_eltern, unt_freunde) %>%
drop_na()
# Check frequencies of geschlecht
table(adolescents_small$geschlecht)
#>
#> männlich weiblich
#> 21 13
# Try exact Wilcoxon test
wilcox.test(unt_freunde ~ geschlecht,
data = adolescents_small,
exact = TRUE,
correct = FALSE)
#> Warning in wilcox.test.default(x = c(4.83333333333333, 6.33333333333333, :
#> cannot compute exact p-value with ties
#>
#> Wilcoxon rank sum test
#>
#> data: unt_freunde by geschlecht
#> W = 73.5, p-value = 0.02489
#> alternative hypothesis: true location shift is not equal to 0Here the t-test for comparison:
t.test(unt_freunde ~ geschlecht, alternative = 'two.sided',
conf.level = .95, var.equal = TRUE,
data = adolescents_small)
#>
#> Two Sample t-test
#>
#> data: unt_freunde by geschlecht
#> t = -2.1998, df = 32, p-value = 0.03516
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -1.45094873 -0.05576678
#> sample estimates:
#> mean in group männlich mean in group weiblich
#> 5.515873 6.269231
The package coin offers advanced options for exact permutation test, including an exact Wilcoxon Rank Sum test when ties are present:
install.packages(coin)
Tests for two independent samples with jmv
library(jmv)
ttestIS(
formula = unt_freunde ~ geschlecht,
data = adolescents_small,
vars = unt_freunde,
bf = TRUE, # Bayes Factor!
welchs = TRUE, # Welch's Test
mann = TRUE, # Wilcoxon / Mann-Whitney
hypothesis = "twoGreater", # 'different' (default),
# 'oneGreater' (group 1 greater than group 2)
# 'twoGreater' (group 2 greater than group 1)
# Equality of Variances (Levene test)
qq = TRUE,
eqv = TRUE, # Levene Test
meanDiff = TRUE,
effectSize = TRUE,
desc = TRUE,
plots = TRUE)
#>
#> INDEPENDENT SAMPLES T-TEST
#>
#> Independent Samples T-Test
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> statistic error % df p Mean difference SE difference Cohen's d
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> unt_freunde Student's t -2.20 32.0 0.018 -0.753 0.342 -0.776
#> Bayes factor₁₀ 3.89 1.50e-6
#> Welch's t -2.28 28.6 0.015 -0.753 0.330 -0.776
#> Mann-Whitney U 73.5 0.013 -0.667 -0.776
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Note. Hₐ männlich < weiblich
#>
#>
#> ASSUMPTIONS
#>
#> Test of Equality of Variances (Levene's)
#> ──────────────────────────────────────────────
#> F df df2 p
#> ──────────────────────────────────────────────
#> unt_freunde 0.676 1 32 0.417
#> ──────────────────────────────────────────────
#> Note. A low p-value suggests a violation
#> of the assumption of equal variances
#>
#>
#> Group Descriptives
#> ─────────────────────────────────────────────────────────────────────
#> Group N Mean Median SD SE
#> ─────────────────────────────────────────────────────────────────────
#> unt_freunde männlich 21 5.52 5.67 1.02 0.223
#> weiblich 13 6.27 6.50 0.875 0.243
#> ─────────────────────────────────────────────────────────────────────

9.2.2 Two dependent samples
Paired samples t-test
For this test we can we can again use the base R function t.test().
As an example, we would like to test whether the extent of the support received from parents unt_parents differs from the extent of the support received from friends unt_freunde across the whole sample.
There are two options: Either we leave the dataset in wide format, where we have unt_eltern and unt_freunde as two variables (columns) in the dataset next to each other.
In this case, the data assignment for the t.test () function is not done using the formula notation but by specifying the two variables to be compared. The only difference to the t-test for independent samples is that we specify the option paired = TRUE (default: paired = FALSE), reflecting the dependence of the data in the two samples/variables.
t.test(adolescents$unt_eltern, adolescents$unt_freunde,
alternative = "two.sided",
conf.level = .95,
paired = TRUE)
#>
#> Paired t-test
#>
#> data: adolescents$unt_eltern and adolescents$unt_freunde
#> t = -0.73804, df = 283, p-value = 0.4611
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.21046776 0.09567902
#> sample estimates:
#> mean of the differences
#> -0.05739437Note that if paired = TRUE would not be specified here, t.test() would assume that the data in the columns unt_eltern and unt_freunde be two independent samples!
The second option is to convert the dataset from wide to long, taking into account that parents and friends are actually two levels of a factor, that is the source of the support (unt_quelle). The measured variable is support (for both factor levels). (The items underlying unt_parents andunt_freunde are exactly the same, they only differ in the reference given to parents or friends.)
library(stringr)
sup_long <- adolescents %>%
drop_na(unt_eltern, unt_freunde) %>%
select(ID, unt_eltern, unt_freunde) %>%
pivot_longer(-ID, names_to = "source", values_to = "support") %>%
mutate(source = str_replace(source, ".*_", "")) %>% # remove unt_
mutate(source = factor(source)) # define as factor
head(sup_long)
#> # A tibble: 6 x 3
#> ID source support
#> <fct> <fct> <dbl>
#> 1 1 eltern 6.67
#> 2 1 freunde 6.67
#> 3 2 eltern 5.17
#> 4 2 freunde 4.83
#> 5 10 eltern 6.83
#> 6 10 freunde 4sup_long %>%
group_by(source) %>%
summarize(mean = mean(support) %>% round(3),
N = length(support))
#> # A tibble: 2 x 3
#> source mean N
#> <fct> <dbl> <int>
#> 1 eltern 5.87 284
#> 2 freunde 5.93 284t.test(support ~ source,
alternative = "two.sided",
conf.level = .95,
paired = TRUE,
data = sup_long)
#>
#> Paired t-test
#>
#> data: support by source
#> t = -0.73804, df = 283, p-value = 0.4611
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.21046776 0.09567902
#> sample estimates:
#> mean of the differences
#> -0.05739437Wilcoxon Signed Rank test
A nonparametric alternative to the paired sample t-test is the Wilcoxon Signed Rank test. This test checks whether the mean rank sums of the negative and positive differences of the two variables are significantly different. Thus, as in the paired sample t-test, a difference variable is created, then ranks are assigned for the absolute values of the differences, and then the mean rank sums are determined separately according to the sign of the respective difference score.
Wilcoxon Signed Rank test is performed by wilcox.test() with the additional argument paired = TRUE.
wilcox.test(adolescents_small$unt_eltern, adolescents_small$unt_freunde,
alternative = "two.sided",
paired = TRUE,
correct = FALSE)
#>
#> Wilcoxon signed rank test
#>
#> data: adolescents_small$unt_eltern and adolescents_small$unt_freunde
#> V = 263.5, p-value = 0.3194
#> alternative hypothesis: true location shift is not equal to 0The test statistic V refers to the rank sum of the positive differences.
Or again using the long dataset and formula notation:
library(stringr)
sup_long_small <- adolescents_small %>%
select(ID, unt_eltern, unt_freunde) %>%
pivot_longer(-ID, names_to = "source", values_to = "support") %>%
mutate(source = str_replace(source, ".*_", "")) %>% # remove unt_
mutate(source = factor(source)) # define as factor
head(sup_long_small)
#> # A tibble: 6 x 3
#> ID source support
#> <fct> <fct> <dbl>
#> 1 1 eltern 6.67
#> 2 1 freunde 6.67
#> 3 2 eltern 5.17
#> 4 2 freunde 4.83
#> 5 10 eltern 6.83
#> 6 10 freunde 4
wilcox.test(support ~ source,
alternative = "two.sided",
paired = TRUE,
correct = FALSE,
data = sup_long_small)
#>
#> Wilcoxon signed rank test
#>
#> data: support by source
#> V = 263.5, p-value = 0.3194
#> alternative hypothesis: true location shift is not equal to 0Paired samples tests with jmv
library(jmv)
ttestPS(
data = adolescents,
pairs = list(
list(
i1="unt_eltern",
i2="unt_freunde")),
bf = TRUE,
wilcoxon = TRUE,
meanDiff = TRUE,
effectSize = TRUE,
ci = TRUE,
desc = TRUE)
#>
#> PAIRED SAMPLES T-TEST
#>
#> Paired Samples T-Test
#> ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> statistic error % df p Mean difference SE difference Lower Upper Cohen's d
#> ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> unt_eltern unt_freunde Student's t -0.738 283 0.461 -0.0574 0.0778 -0.210 0.0957 -0.0438
#> Bayes factor₁₀ 0.0871 5.88e-4
#> Wilcoxon W 16477 0.934 -5.29e-5 0.0778 -0.167 0.167 -0.0438
#> ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#>
#>
#> Descriptives
#> ───────────────────────────────────────────────────────────
#> N Mean Median SD SE
#> ───────────────────────────────────────────────────────────
#> unt_eltern 284 5.87 6.17 0.999 0.0593
#> unt_freunde 284 5.93 6.08 0.963 0.0571
#> ───────────────────────────────────────────────────────────9.3 More than two groups
9.3.1 Multiple independent groups
One-way analysis of variance
We perform a one-way ANOVA with the grade average Gesamtnote as a dependent variable and the level of education of the father (bildung_vater) as a factor (independent variable). The null hypothesis is that the means of the grade average do not differ between groups of adolescents whose fathers have different levels of education.
First, we create a data set grades containing only the variables ID,gesamtnote, bildung_vater and geschlecht (for later analysis) and remove all observations with missing values.
grades <- adolescents %>%
select(ID, Gesamtnote, bildung_vater, geschlecht) %>%
drop_na()
grades
#> # A tibble: 264 x 4
#> ID Gesamtnote bildung_vater geschlecht
#> <fct> <dbl> <fct> <fct>
#> 1 2 4 Abitur männlich
#> 2 10 5 Realschule weiblich
#> 3 11 4 Realschule weiblich
#> 4 12 5 Hochschule weiblich
#> 5 14 4 Realschule männlich
#> 6 15 4 Realschule männlich
#> # … with 258 more rowsFirst, let’s look at some descriptive statistics (means and standard deviations) using summarise():
grades %>%
group_by(bildung_vater) %>%
summarise(mean = round(mean(Gesamtnote, na.rm = TRUE), 2),
sd = round(sd(Gesamtnote, na.rm = TRUE), 2),
N = length(Gesamtnote))
#> # A tibble: 4 x 4
#> bildung_vater mean sd N
#> <fct> <dbl> <dbl> <int>
#> 1 Hauptschule 4.05 0.67 41
#> 2 Realschule 4.38 0.65 93
#> 3 Abitur 4.5 0.65 39
#> 4 Hochschule 4.69 0.68 91Descriptively, higher educational levels of the father are related to a higher overall grade average of students.
The standard deviations of the DV seem to be similar across groups. leveneTest() is used to test the assumption of homogeneity of variances.
library(car)
leveneTest(grades$Gesamtnote, grades$bildung_vater,
center = median)
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 3 0.4906 0.6891
#> 260The non-significance of the Levene test allows to maintain the assumption of homoscedasticity.
Now we can compute the ANOVA using the aov() function, save the output in a results object and then use the summary() function to access the output. aov() is a wrapper function for the more general lm() function (linear model, see next chapter) designed to extract the relevant information for an ANOVA-type of analysis (which is based on a general linear model or GLM).
The TukeyHSD function can be used to get all pairwise comparisons (adjusted confidence intervals and Tukey \(p\)-values).
anova1 <- aov(Gesamtnote ~ bildung_vater, data = grades)
summary(anova1)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> bildung_vater 3 12.36 4.120 9.272 7.58e-06 ***
#> Residuals 260 115.53 0.444
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
TukeyHSD(anova1, ordered = TRUE)
#> Tukey multiple comparisons of means
#> 95% family-wise confidence level
#> factor levels have been ordered
#>
#> Fit: aov(formula = Gesamtnote ~ bildung_vater, data = grades)
#>
#> $bildung_vater
#> diff lwr upr p adj
#> Realschule-Hauptschule 0.3269866 0.003864173 0.6501091 0.0461134
#> Abitur-Hauptschule 0.4437774 0.058237843 0.8293169 0.0167437
#> Hochschule-Hauptschule 0.6397481 0.315540988 0.9639551 0.0000039
#> Abitur-Realschule 0.1167907 -0.212031612 0.4456131 0.7950495
#> Hochschule-Realschule 0.3127614 0.058608643 0.5669142 0.0088548
#> Hochschule-Abitur 0.1959707 -0.133917530 0.5258589 0.4174570Beside the TukeyHSD() function there is another way to obtain post-hoc pairwise comparisons: pairwise.t.test()
Among others, the methods p.adjust.method = c("bonferroni", "holm") are available. The pairwise.t.test() function works independently of the ANOVA procedure (it performs pairwise adjusted t-tests without an overall test).
pairwise.t.test(grades$Gesamtnote, grades$bildung_vater,
p.adjust.method = "holm", data = grades)
#>
#> Pairwise comparisons using t tests with pooled SD
#>
#> data: grades$Gesamtnote and grades$bildung_vater
#>
#> Hauptschule Realschule Abitur
#> Realschule 0.0282 - -
#> Abitur 0.0128 0.3593 -
#> Hochschule 3.9e-06 0.0082 0.2515
#>
#> P value adjustment method: holmOne-way ANOVA in jmv: Like SPSS, jmv provides different procedures (and syntax) for one-way and factorial ANOVA.
anovaOneW(
formula = Gesamtnote ~ bildung_vater,
data = adolescents,
fishers = TRUE,
desc = TRUE,
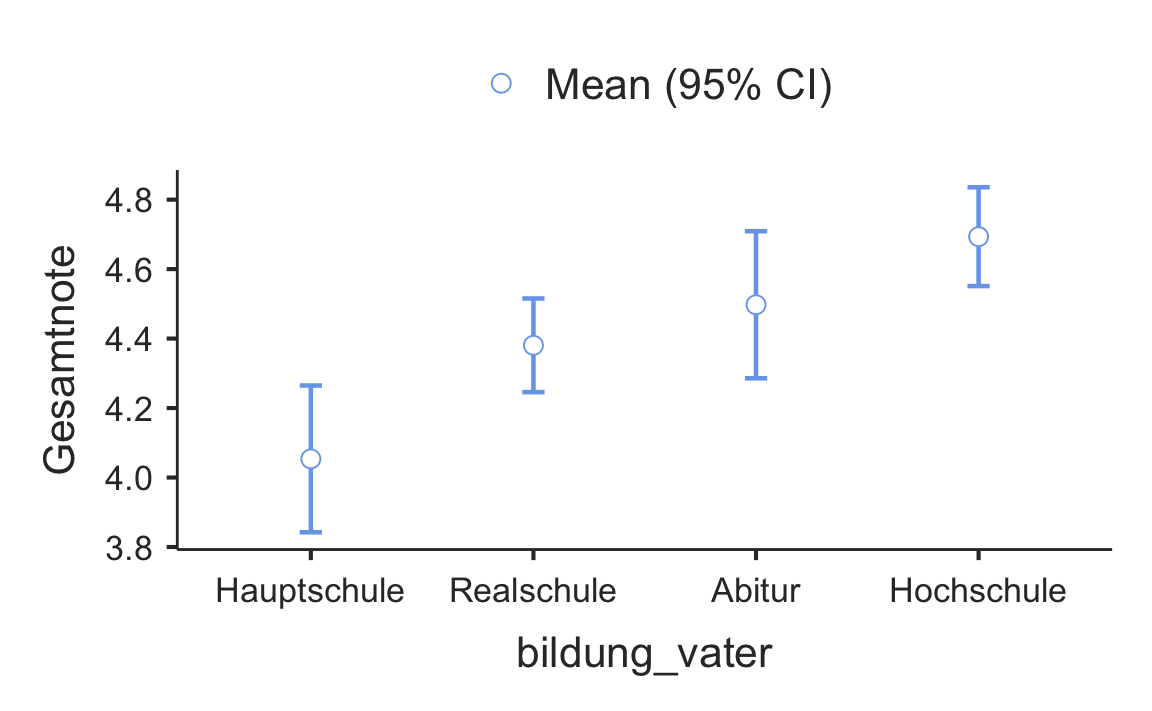
descPlot = TRUE,
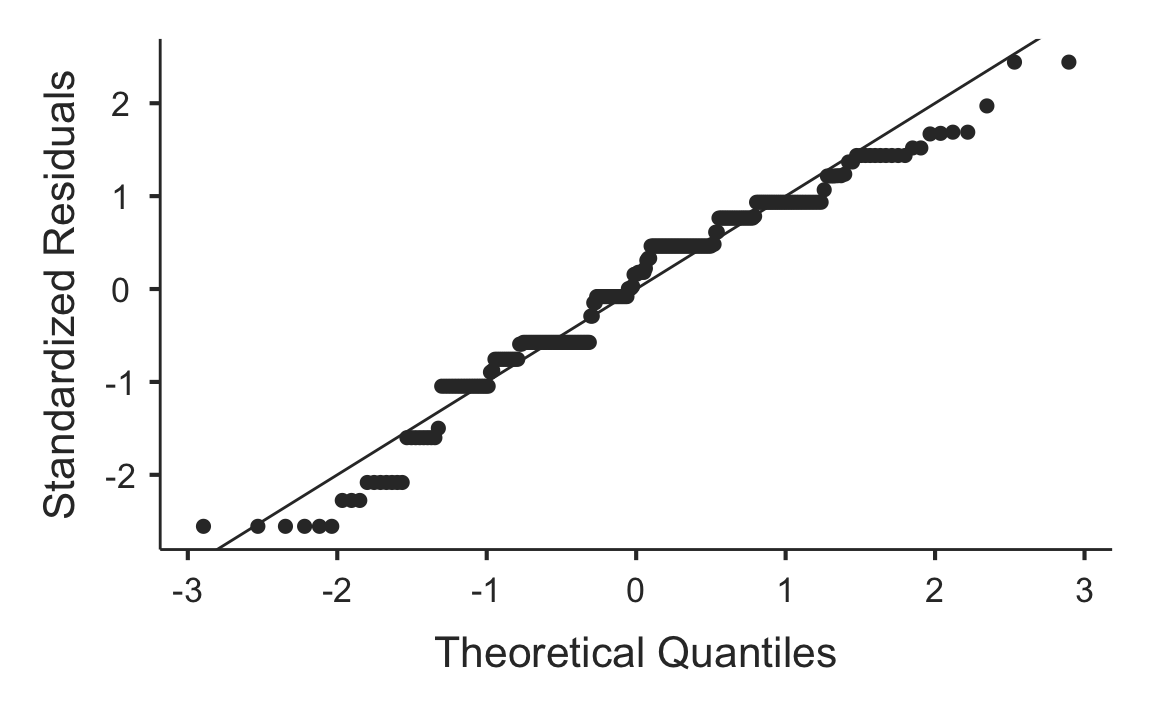
qq = TRUE,
eqv = TRUE,
phMethod = "tukey",
phTest = TRUE)
#>
#> ONE-WAY ANOVA
#>
#> One-Way ANOVA
#> ──────────────────────────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────────────────────────
#> Gesamtnote Welch's 8.95 3 108 < .001
#> Fisher's 9.27 3 260 < .001
#> ──────────────────────────────────────────────────────────
#>
#>
#> Group Descriptives
#> ────────────────────────────────────────────────────────────────
#> bildung_vater N Mean SD SE
#> ────────────────────────────────────────────────────────────────
#> Gesamtnote Hauptschule 41 4.05 0.669 0.1045
#> Realschule 93 4.38 0.655 0.0679
#> Abitur 39 4.50 0.653 0.1046
#> Hochschule 91 4.69 0.683 0.0716
#> ────────────────────────────────────────────────────────────────
#>
#>
#> ASSUMPTION CHECKS
#>
#> Test for Equality of Variances (Levene's)
#> ──────────────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────────────
#> Gesamtnote 0.603 3 260 0.613
#> ──────────────────────────────────────────────
#>
#>
#> POST HOC TESTS
#>
#> Tukey Post-Hoc Test – Gesamtnote
#> ───────────────────────────────────────────────────────────────────────────────────────
#> Hauptschule Realschule Abitur Hochschule
#> ───────────────────────────────────────────────────────────────────────────────────────
#> Hauptschule Mean difference — -0.327 -0.444 -0.640
#> t-value — -2.62 -2.976 -5.10
#> df — 260 260 260
#> p-value — 0.046 0.017 < .001
#>
#> Realschule Mean difference — -0.117 -0.313
#> t-value — -0.918 -3.18
#> df — 260 260
#> p-value — 0.795 0.009
#>
#> Abitur Mean difference — -0.196
#> t-value — -1.54
#> df — 260
#> p-value — 0.417
#>
#> Hochschule Mean difference —
#> t-value —
#> df —
#> p-value —
#> ───────────────────────────────────────────────────────────────────────────────────────
Kruskal-Wallis test (H-test)
The H-test is a nonparametric alternative to the one-way analysis of variance. It is an extension of the Wilcoxon rank sum test to multiple samples. The Kruskal-Wallis test is usually carried out asymptotically, since an exact test requires a lot of computing power - at least with larger samples - and is usually not necessary.
First, let’s get the medians using dplyr:
grades %>%
group_by(bildung_vater) %>%
summarise(median = median(Gesamtnote))
#> # A tibble: 4 x 2
#> bildung_vater median
#> <fct> <dbl>
#> 1 Hauptschule 4
#> 2 Realschule 4
#> 3 Abitur 4.6
#> 4 Hochschule 5The Kruskal-Wallis H test is obtained by:
kruskal.test(Gesamtnote ~ bildung_vater, data = grades)
#>
#> Kruskal-Wallis rank sum test
#>
#> data: Gesamtnote by bildung_vater
#> Kruskal-Wallis chi-squared = 29.008, df = 3, p-value = 2.231e-06A box-plot illustrates the median differences:
grades %>%
ggplot(aes(x = bildung_vater, y = Gesamtnote)) +
geom_boxplot() +
geom_jitter(width = 0.1) +
xlab("Bildung des Vaters") +
theme_classic()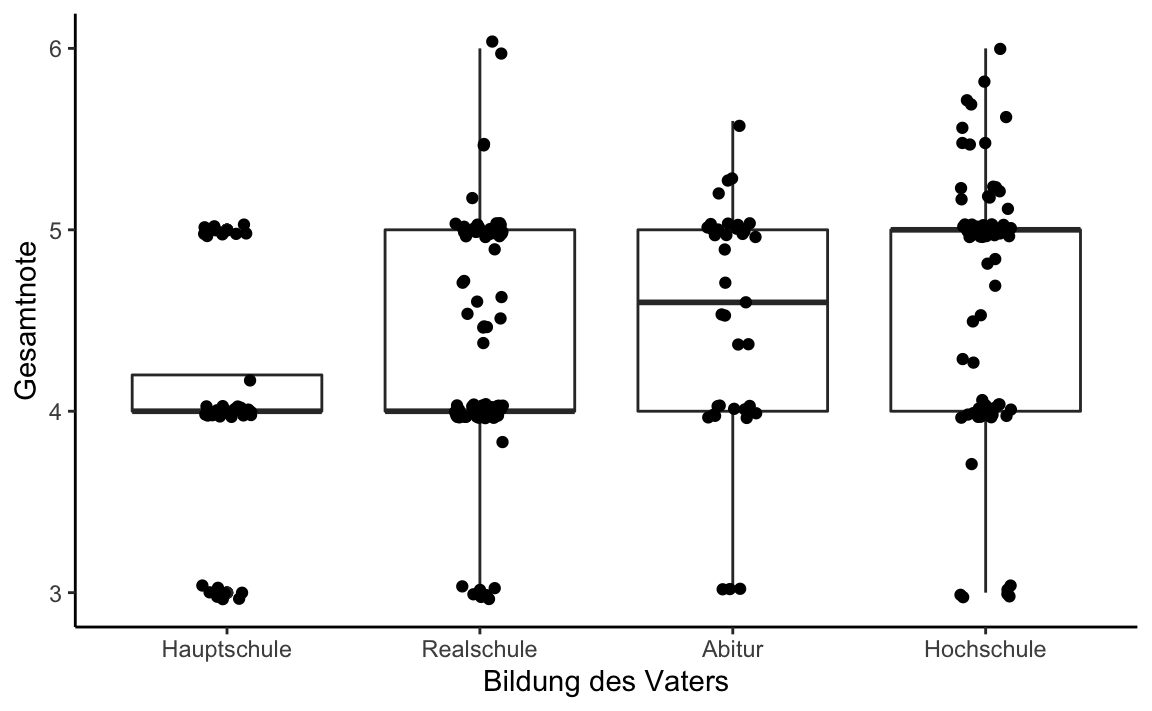
The Kruskal-Wallis test can also be performed by anovaNP() from the jmv package. It includes a method for post-hoc comparisons for pairs of groups:
library(jmv)
anovaNP(
formula = Gesamtnote ~ bildung_vater,
data = grades,
es = TRUE,
pairs = TRUE)
#>
#> ONE-WAY ANOVA (NON-PARAMETRIC)
#>
#> Kruskal-Wallis
#> ───────────────────────────────────────────────
#> χ² df p ε²
#> ───────────────────────────────────────────────
#> Gesamtnote 29.0 3 < .001 0.110
#> ───────────────────────────────────────────────
#>
#>
#> DWASS-STEEL-CRITCHLOW-FLIGNER PAIRWISE COMPARISONS
#>
#> Pairwise comparisons - Gesamtnote
#> ───────────────────────────────────────────────
#> W p
#> ───────────────────────────────────────────────
#> Hauptschule Realschule 3.38 0.079
#> Hauptschule Abitur 4.16 0.017
#> Hauptschule Hochschule 6.76 < .001
#> Realschule Abitur 1.75 0.603
#> Realschule Hochschule 5.31 0.001
#> Abitur Hochschule 2.57 0.266
#> ───────────────────────────────────────────────Factorial ANOVA
We would like to analyse the joint effect of two factors on adolescents’ grade average: A) educational level of the father (bildung_vater) and B) gender (geschlecht) .
Again, let’s first look at descriptive statistics using summarise():
grades %>%
group_by(bildung_vater, geschlecht) %>%
summarise(mean = round(mean(Gesamtnote, na.rm = TRUE), 2),
sd = round(sd(Gesamtnote, na.rm = TRUE), 3),
var = round(var(Gesamtnote, na.rm = TRUE), 3),
N = length(Gesamtnote))
#> # A tibble: 8 x 6
#> # Groups: bildung_vater [4]
#> bildung_vater geschlecht mean sd var N
#> <fct> <fct> <dbl> <dbl> <dbl> <int>
#> 1 Hauptschule männlich 3.86 0.64 0.409 22
#> 2 Hauptschule weiblich 4.27 0.651 0.423 19
#> 3 Realschule männlich 4.13 0.626 0.392 48
#> 4 Realschule weiblich 4.65 0.578 0.334 45
#> 5 Abitur männlich 4.39 0.694 0.481 21
#> 6 Abitur weiblich 4.63 0.595 0.354 18
#> # … with 2 more rows
grades %>%
group_by(geschlecht) %>%
summarise(mean = round(mean(Gesamtnote, na.rm = TRUE), 2),
sd = round(sd(Gesamtnote, na.rm = TRUE), 3),
var = round(var(Gesamtnote, na.rm = TRUE), 3),
N = length(Gesamtnote))
#> # A tibble: 2 x 5
#> geschlecht mean sd var N
#> <fct> <dbl> <dbl> <dbl> <int>
#> 1 männlich 4.29 0.723 0.522 145
#> 2 weiblich 4.65 0.612 0.375 119Then we carry out the Levene test to check the homoscadasticity assumption:
library(car)
leveneTest(grades$Gesamtnote ~ grades$bildung_vater*grades$geschlecht,
center = median)
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 7 1.1221 0.3495
#> 256First, we perform the two-factorial analysis of variance using aov():
anova2 <- aov(Gesamtnote ~ bildung_vater*geschlecht, data = grades)
Anova(anova2, type = 3)
#> Anova Table (Type III tests)
#>
#> Response: Gesamtnote
#> Sum Sq Df F value Pr(>F)
#> (Intercept) 328.41 1 799.1587 < 2.2e-16 ***
#> bildung_vater 9.90 3 8.0335 3.891e-05 ***
#> geschlecht 1.71 1 4.1714 0.04214 *
#> bildung_vater:geschlecht 0.85 3 0.6875 0.56041
#> Residuals 105.20 256
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1For factorial ANOVAS it is essential to request the summary of the ANOVA object using Anova() from the car package. Only this way Type II or Type III sums of squares (type = 2 ortype = 3) can be obtained. summary() only returns Type I sums of squares (no further option).
The most common method (and the one known from SPSS) is Type III sums of squares where all levels of effect terms are partialled for each other (in terms of cell frequencies in unbalanced designs). The default for Anova() is type = 2 since some important developers for statistical analyses in R prefer Type II sums of squares that return marginal sums of squares for lower order effects (not partialled for higher order effects; here: main effects independent of the interaction effect). Finally, Type I sums of squares return a sequential partialization of all effects (including those of the same order; here: only the main effect that enters the model second is partialled for the one entered first, but not the other way round as in Type II).
Let’s look at the differences:
anova3 <- aov(Gesamtnote ~ bildung_vater*geschlecht, data = grades)
Anova(anova3, type = 2)
#> Anova Table (Type II tests)
#>
#> Response: Gesamtnote
#> Sum Sq Df F value Pr(>F)
#> bildung_vater 13.421 3 10.8863 9.380e-07 ***
#> geschlecht 9.484 1 23.0781 2.651e-06 ***
#> bildung_vater:geschlecht 0.848 3 0.6875 0.5604
#> Residuals 105.202 256
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# anova3 has the same sum of squares as the following main effect only model:
anova4 <- aov(Gesamtnote ~ bildung_vater + geschlecht, data = grades)
Anova(anova4, type = 2)
#> Anova Table (Type II tests)
#>
#> Response: Gesamtnote
#> Sum Sq Df F value Pr(>F)
#> bildung_vater 13.421 3 10.926 8.827e-07 ***
#> geschlecht 9.484 1 23.162 2.533e-06 ***
#> Residuals 106.049 259
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Sequential partialling (Type I) A:
anova5 <- aov(Gesamtnote ~ bildung_vater*geschlecht, data = grades)
summary(anova5)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> bildung_vater 3 12.36 4.120 10.026 2.86e-06 ***
#> geschlecht 1 9.48 9.484 23.078 2.65e-06 ***
#> bildung_vater:geschlecht 3 0.85 0.283 0.687 0.56
#> Residuals 256 105.20 0.411
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Sequential partialling (Type I) B:
anova6 <- aov(Gesamtnote ~ geschlecht*bildung_vater, data = grades)
summary(anova6)
#> Df Sum Sq Mean Sq F value Pr(>F)
#> geschlecht 1 8.42 8.424 20.498 9.15e-06 ***
#> bildung_vater 3 13.42 4.474 10.886 9.38e-07 ***
#> geschlecht:bildung_vater 3 0.85 0.283 0.687 0.56
#> Residuals 256 105.20 0.411
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Factorial ANOVA with jmv includes options for contrast analysis and post-hoc comparisons (unfortunately the post-hoc comparisons do not work in this online script but they do work when used in a regular R script or Rmd-File, try it!)
ANOVA(
formula = Gesamtnote ~ bildung_vater + geschlecht + bildung_vater:geschlecht,
data = adolescents,
effectSize = c("eta", "partEta", "omega"),
homo = TRUE,
contrasts = list(
list(
var="bildung_vater",
type="helmert"),
list(
var="geschlecht",
type="none")))
#>
#> ANOVA
#>
#> ANOVA
#> ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Sum of Squares df Mean Square F p η² η²p ω²
#> ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> bildung_vater 12.717 3 4.239 10.315 < .001 0.101 0.108 0.091
#> geschlecht 7.316 1 7.316 17.802 < .001 0.058 0.065 0.055
#> bildung_vater:geschlecht 0.848 3 0.283 0.687 0.560 0.007 0.008 -0.003
#> Residuals 105.202 256 0.411
#> ────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#>
#>
#> ASSUMPTION CHECKS
#>
#> Homogeneity of Variances (Levene's)
#> ───────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────
#> 1.54 7 256 0.154
#> ───────────────────────────────────
#>
#>
#> CONTRASTS
#>
#> Contrasts - bildung_vater
#> ─────────────────────────────────────────────────────────────────────────────────────────
#> Estimate SE t p
#> ─────────────────────────────────────────────────────────────────────────────────────────
#> Hauptschule - Realschule, Abitur, Hochschule -0.470 0.1108 -4.24 < .001
#> Realschule - Abitur, Hochschule -0.224 0.0908 -2.47 0.014
#> Abitur - Hochschule -0.213 0.1236 -1.73 0.086
#> ─────────────────────────────────────────────────────────────────────────────────────────
# postHoc = ~ bildung_vater:geschlecht,
# postHocCorr = c("none", "bonf", "holm"))9.3.2 Multiple dependent groups
(One-way) repeated measures ANOVA
As an example, let’s look at the fictitious study on “Honeymoon or Hangover” (using an example from the book by [Budischewski & Kriens, 2012] (https://www.beltz.de/fachmedien/psychologie/books/produkt_produktdetails/4144-aufgabensammlung_statistik.html). In this study, \(n = 10\) employees from two companies (\(n = 5\) each) were interviewed at the beginning of their employment (Anfang) as well as at two further measurement points (Drei Monate, Sechs Monate) regarding their job satisfaction (Zufriedenheit). The hypothesis was that employees are very satisfied at the beginning, as they enthusiastically approach the new task (“honeymoon”), then due to the heavy workload at a new entry a phase of lesser satisfaction follows (“hangover”) before satisfaction levels off again (here after six months). In general, we ask about the differences in the mean values of job satisfaction over time. We start with only one company (company 1).
For the Repeated Measures ANOVA we have to create long format dataset first. Let’s import the SPSS dataset honeymoon_hangover_2companies.sav and then use the pivot_longer() function from tidyr to convert from wide to long.
library(haven)
Honeymoon <- read_sav("data/honeymoon_hangover_2Firmen.sav")
Honeymoon$ID <- as.factor(Honeymoon$ID)
Honeymoon$Firma <- as.factor(Honeymoon$Firma)
Honeymoon
#> # A tibble: 10 x 5
#> ID Firma Anfang Drei_Monate Sechs_Monate
#> <fct> <fct> <dbl> <dbl> <dbl>
#> 1 1 1 9 4 5
#> 2 2 1 9 4 8
#> 3 3 1 9 7 14
#> 4 4 1 10 9 5
#> 5 5 1 8 1 3
#> 6 6 2 10 10 10
#> # … with 4 more rowsHoneymoon_long <- Honeymoon %>%
pivot_longer(-c(ID, Firma), names_to = "Messzeitpunkt", values_to = "Zufriedenheit"
) %>%
mutate(Messzeitpunkt = factor(Messzeitpunkt)) %>%
arrange(Firma, ID)
Honeymoon_long
#> # A tibble: 30 x 4
#> ID Firma Messzeitpunkt Zufriedenheit
#> <fct> <fct> <fct> <dbl>
#> 1 1 1 Anfang 9
#> 2 1 1 Drei_Monate 4
#> 3 1 1 Sechs_Monate 5
#> 4 2 1 Anfang 9
#> 5 2 1 Drei_Monate 4
#> 6 2 1 Sechs_Monate 8
#> # … with 24 more rowsLet’s get the means of the DV:
Honeymoon_long %>%
group_by(Firma, Messzeitpunkt) %>%
summarise(Bedingungsmittelwert = mean(Zufriedenheit))
#> # A tibble: 6 x 3
#> # Groups: Firma [2]
#> Firma Messzeitpunkt Bedingungsmittelwert
#> <fct> <fct> <dbl>
#> 1 1 Anfang 9
#> 2 1 Drei_Monate 5
#> 3 1 Sechs_Monate 7
#> 4 2 Anfang 10
#> 5 2 Drei_Monate 10.8
#> 6 2 Sechs_Monate 11First, we only want to examine the development of job satisfaction in the first company:
First, let’s use the classic aov() method again:
rm_anova <- aov(Zufriedenheit ~ Messzeitpunkt + Error(ID/Messzeitpunkt), data = Honeymoon_long_F1)
summary(rm_anova)
#>
#> Error: ID
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Residuals 4 60 15
#>
#> Error: ID:Messzeitpunkt
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Messzeitpunkt 2 40 20.00 2.963 0.109
#> Residuals 8 54 6.75The package ezANOVA() provides more functionality for repeated measures ANOVAs, including shericity tests and corrections:
install.packages("ez")
library(ez)
#> Registered S3 methods overwritten by 'lme4':
#> method from
#> cooks.distance.influence.merMod car
#> influence.merMod car
#> dfbeta.influence.merMod car
#> dfbetas.influence.merMod car
ezANOVA(Honeymoon_long_F1, dv = Zufriedenheit,
wid = ID, within = Messzeitpunkt,
detailed = TRUE)
#> $ANOVA
#> Effect DFn DFd SSn SSd F p p<.05 ges
#> 1 (Intercept) 1 4 735 60 49.000000 0.00219213 * 0.8657244
#> 2 Messzeitpunkt 2 8 40 54 2.962963 0.10890896 0.2597403
#>
#> $`Mauchly's Test for Sphericity`
#> Effect W p p<.05
#> 2 Messzeitpunkt 0.6872428 0.569725
#>
#> $`Sphericity Corrections`
#> Effect GGe p[GG] p[GG]<.05 HFe p[HF] p[HF]<.05
#> 2 Messzeitpunkt 0.7617555 0.1308327 1.134177 0.108909Since the Mauchly test is not significant, we can maintain the null hypothesis of a spherical variance-covariance matrix (sphericity assumption) and therefore do not need to make any corrections.
The effect of the factor Messzeitpunkt is not significant. Our very small sample of n = 5 is associated with a very low statistical power, though.
Because of the low power of the Mauchly test we could still apply the corrections according to Greenhouse Geisser-\(\epsilon\) (GGe) or Huynh-Feldt-$$ (HFe): also the p[GG] and p[HF] are both non-significant.
\(~\)
Post-hoc tests can be obtained using the pairwise.t.test() from stats, where we have to specify paired = TRUE. Here we use both the uncorrected pairwise comparisons (p.adjust.method = "none") and the Bonferroni-Holm corrected comparisons (p.adjust.method = "holm"). This is done for demonstration purposes even though the overall effect was non-significant.
pairwise.t.test(Honeymoon_long_F1$Zufriedenheit,
Honeymoon_long_F1$Messzeitpunkt,
p.adjust.method = "none",
paired = TRUE,
data = Honeymoon_long_F1)
#>
#> Pairwise comparisons using paired t tests
#>
#> data: Honeymoon_long_F1$Zufriedenheit and Honeymoon_long_F1$Messzeitpunkt
#>
#> Anfang Drei_Monate
#> Drei_Monate 0.022 -
#> Sechs_Monate 0.351 0.333
#>
#> P value adjustment method: none
pairwise.t.test(Honeymoon_long_F1$Zufriedenheit,
Honeymoon_long_F1$Messzeitpunkt,
p.adjust.method = "holm",
paired = TRUE,
data = Honeymoon_long_F1)
#>
#> Pairwise comparisons using paired t tests
#>
#> data: Honeymoon_long_F1$Zufriedenheit and Honeymoon_long_F1$Messzeitpunkt
#>
#> Anfang Drei_Monate
#> Drei_Monate 0.065 -
#> Sechs_Monate 0.665 0.665
#>
#> P value adjustment method: holmWe can do the RM ANOVA also with jmv. In jmv we need a wide dataset again since part of the philosophy of jmv and [jamovi] (https://www.jamovi.org) is to provide similar functionality to former SPSS users.
Let’s select company 1 from the Honeymooon_wide dataset:
The syntax of the jmv::anovaRM() function is quite complicated (because of the untidy wide dataset):
anovaRM(
data = Honeymoon_wide_F1,
rm = list( # Definition of RM factor / factor levels
list(
label = "Messzeitpunkt",
levels = c("Anfang", "Drei_Monate", "Sechs_Monate"))),
rmCells = list( # Assignment of the DV (measure)
list( # to the cells (factor levels)
measure = "Anfang",
cell = "Anfang"),
list(
measure = "Drei_Monate",
cell = "Drei_Monate"),
list(
measure = "Sechs_Monate",
cell = "Sechs_Monate")),
rmTerms = list( # Calling those RM model terms that should
"Messzeitpunkt"), # be used in the current model
effectSize = c("eta", "omega"),
spherTests = TRUE,
spherCorr = c("none", "GG", "HF"))
#>
#> REPEATED MEASURES ANOVA
#>
#> Within Subjects Effects
#> ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Sphericity Correction Sum of Squares df Mean Square F p η² ω²
#> ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Messzeitpunkt None 40.0 2 20.00 2.96 0.109 0.260 0.165
#> Greenhouse-Geisser 40.0 1.52 26.26 2.96 0.131 0.260 0.165
#> Huynh-Feldt 40.0 2.00 20.00 2.96 0.109 0.260 0.165
#>
#> Residual None 54.0 8 6.75
#> Greenhouse-Geisser 54.0 6.09 8.86
#> Huynh-Feldt 54.0 8.00 6.75
#> ──────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Note. Type 3 Sums of Squares
#>
#>
#> Between Subjects Effects
#> ───────────────────────────────────────────────────────────────────────────────────
#> Sum of Squares df Mean Square F p η² ω²
#> ───────────────────────────────────────────────────────────────────────────────────
#> Residual 60.0 4 15.0
#> ───────────────────────────────────────────────────────────────────────────────────
#> Note. Type 3 Sums of Squares
#>
#>
#> ASSUMPTIONS
#>
#> Tests of Sphericity
#> ──────────────────────────────────────────────────────────────────────────────────
#> Mauchly's W p Greenhouse-Geisser ε Huynh-Feldt ε
#> ──────────────────────────────────────────────────────────────────────────────────
#> Messzeitpunkt 0.687 0.570 0.762 1.00
#> ──────────────────────────────────────────────────────────────────────────────────Friedman Repeated Measures ANOVA for Rank Data
The Friedman test is a nonparametric alternative to the repeated measures ANOVA. It is an extension of the Wilcoxon signed rank test to multiple connected samples. The Friedman test is usually performed asymptotically, because an exact test requires quite some computing power (with large samples).
Unfortunately, the Friedman test does not work with ID being a factor, so we have to convert ID into a numeric vector first.
Honeymoon_long_F1$ID <- as.numeric(Honeymoon_long_F1$ID)
friedman.test(Zufriedenheit ~ Messzeitpunkt | ID,
data = Honeymoon_long_F1)
#>
#> Friedman rank sum test
#>
#> data: Zufriedenheit and Messzeitpunkt and ID
#> Friedman chi-squared = 6.4, df = 2, p-value = 0.04076Let’s look at the median differences using box plot:
Honeymoon_long_F1 %>%
ggplot(aes(x = Messzeitpunkt, y = Zufriedenheit)) +
geom_boxplot() +
geom_point() +
theme_classic()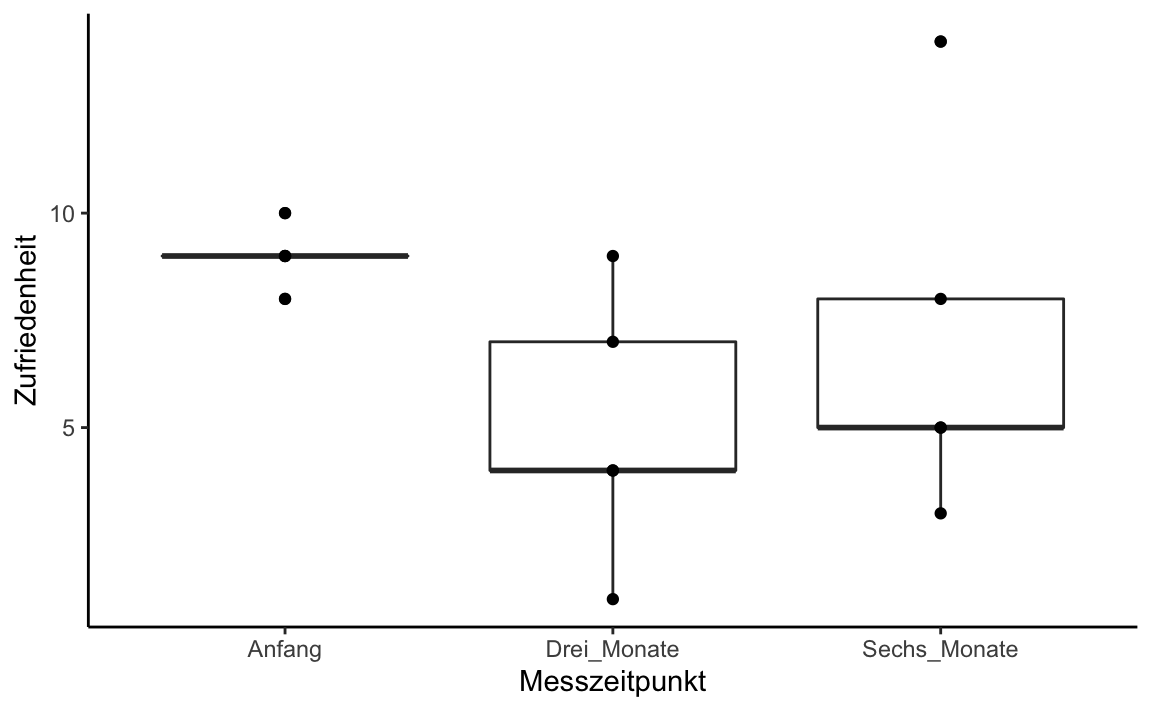
\(~\)
The Friedman test is also in jmv. For anovaRMNP() we need the wide data set again:
library(jmv)
anovaRMNP(
data = Honeymoon_wide_F1,
measures = vars(Anfang, Drei_Monate, Sechs_Monate),
pairs = TRUE,
plots = TRUE,
plotType = "medians")
#>
#> REPEATED MEASURES ANOVA (NON-PARAMETRIC)
#>
#> Friedman
#> ───────────────────────
#> χ² df p
#> ───────────────────────
#> 6.40 2 0.041
#> ───────────────────────
#>
#>
#> Pairwise Comparisons (Durbin-Conover)
#> ──────────────────────────────────────────────────────────
#> Statistic p
#> ──────────────────────────────────────────────────────────
#> Anfang - Drei_Monate 3.77 0.005
#> Anfang - Sechs_Monate 1.89 0.096
#> Drei_Monate - Sechs_Monate 1.89 0.096
#> ──────────────────────────────────────────────────────────
Mixed (within-between) design ANOVA
We now want to compare the development of job satisfaction across the two companies.
Honeymoon_long %>%
group_by(Firma, Messzeitpunkt) %>%
summarise(Bedingungsmittelwert = mean(Zufriedenheit))
#> # A tibble: 6 x 3
#> # Groups: Firma [2]
#> Firma Messzeitpunkt Bedingungsmittelwert
#> <fct> <fct> <dbl>
#> 1 1 Anfang 9
#> 2 1 Drei_Monate 5
#> 3 1 Sechs_Monate 7
#> 4 2 Anfang 10
#> 5 2 Drei_Monate 10.8
#> 6 2 Sechs_Monate 11With aov() the mixed-design ANOVA is obtained by:
mixed_anova <- aov(Zufriedenheit ~ Firma*Messzeitpunkt + Error(ID/Messzeitpunkt), data = Honeymoon_long)
summary(mixed_anova)
#>
#> Error: ID
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Firma 1 97.2 97.20 8.877 0.0176 *
#> Residuals 8 87.6 10.95
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Error: ID:Messzeitpunkt
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Messzeitpunkt 2 13.4 6.700 1.874 0.1857
#> Firma:Messzeitpunkt 2 29.4 14.700 4.112 0.0362 *
#> Residuals 16 57.2 3.575
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
There are aov() formula notations for more ad advanced ANOVA designs (http://www.cookbook-r.com/Statistical_analysis/ANOVA/):
Two withinfactors ww_anova <- aov(y ~ RM1RM2 + Error(subject/(w1w2)), data = data_long)
One between factor and two within factors bww_anova <- aov(y ~ b1w1w2 + Error(subject/(w1*w2)) + b1, data=data_long)
Two between factors and one within factor bww_anova <- aov(y ~ b1b2w1 + Error(subject/(w1)) + b1*b2, data=data_long)
With ezANOVA() the mixed-design ANOVA is obtained by defining the variable Messzeitpunkt as within-factor and Firma as between-factor:
library(ez)
ezANOVA(Honeymoon_long, dv = Zufriedenheit,
wid = ID, within = Messzeitpunkt,
between = Firma, detailed = TRUE)
#> $ANOVA
#> Effect DFn DFd SSn SSd F p p<.05
#> 1 (Intercept) 1 8 2323.2 87.6 212.164384 4.837731e-07 *
#> 2 Firma 1 8 97.2 87.6 8.876712 1.761704e-02 *
#> 3 Messzeitpunkt 2 16 13.4 57.2 1.874126 1.856652e-01
#> 4 Firma:Messzeitpunkt 2 16 29.4 57.2 4.111888 3.622639e-02 *
#> ges
#> 1 0.94132901
#> 2 0.40165289
#> 3 0.08470291
#> 4 0.16877153
#>
#> $`Mauchly's Test for Sphericity`
#> Effect W p p<.05
#> 3 Messzeitpunkt 0.7122598 0.3049541
#> 4 Firma:Messzeitpunkt 0.7122598 0.3049541
#>
#> $`Sphericity Corrections`
#> Effect GGe p[GG] p[GG]<.05 HFe p[HF]
#> 3 Messzeitpunkt 0.7765541 0.19689735 0.9289728 0.18928790
#> 4 Firma:Messzeitpunkt 0.7765541 0.05071043 0.9289728 0.04029652
#> p[HF]<.05
#> 3
#> 4 *To do this in jmv we need the wide data set again (Honeymoon, including both companies).
We get the mixed-design ANOVA by adding the arguments bs = 'Firma' (definition of the between subjects factor) and bsTerms = "Firma" to the previous code for the RM ANOVA. The latter argument indicates which of the factors listed under bs should be used in the model. The interaction effect between the bs factor and the rm factor is included automatically.
anovaRM(
data = Honeymoon,
rm = list( # Definition of RM factor / factor levels
list(
label = "Messzeitpunkt",
levels = c("Anfang", "Drei_Monate", "Sechs_Monate"))),
rmCells = list( # Assignment of the DV (measure)
list( # to the cells (factor levels)
measure = "Anfang",
cell = "Anfang"),
list(
measure = "Drei_Monate",
cell = "Drei_Monate"),
list(
measure = "Sechs_Monate",
cell = "Sechs_Monate")),
rmTerms = list( # Calling those RM model terms that should
"Messzeitpunkt"), # be used in the current model
bs = "Firma", # Definition of between factor
bsTerms = list( # Calling those "between" model terms that should
"Firma"), # be used in the current model
effectSize = c("eta", "omega"),
spherTests = TRUE,
spherCorr = c("none", "GG", "HF"))
#>
#> REPEATED MEASURES ANOVA
#>
#> Within Subjects Effects
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Sphericity Correction Sum of Squares df Mean Square F p η² ω²
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Messzeitpunkt None 13.4 2 6.70 1.87 0.186 0.047 0.022
#> Greenhouse-Geisser 13.4 1.55 8.63 1.87 0.197 0.047 0.022
#> Huynh-Feldt 13.4 1.86 7.21 1.87 0.189 0.047 0.022
#>
#> Messzeitpunkt:Firma None 29.4 2 14.70 4.11 0.036 0.103 0.077
#> Greenhouse-Geisser 29.4 1.55 18.93 4.11 0.051 0.103 0.077
#> Huynh-Feldt 29.4 1.86 15.82 4.11 0.040 0.103 0.077
#>
#> Residual None 57.2 16 3.58
#> Greenhouse-Geisser 57.2 12.42 4.60
#> Huynh-Feldt 57.2 14.86 3.85
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> Note. Type 3 Sums of Squares
#>
#>
#> Between Subjects Effects
#> ──────────────────────────────────────────────────────────────────────────────────────
#> Sum of Squares df Mean Square F p η² ω²
#> ──────────────────────────────────────────────────────────────────────────────────────
#> Firma 97.2 1 97.2 8.88 0.018 0.341 0.292
#> Residual 87.6 8 10.9
#> ──────────────────────────────────────────────────────────────────────────────────────
#> Note. Type 3 Sums of Squares
#>
#>
#> ASSUMPTIONS
#>
#> Tests of Sphericity
#> ──────────────────────────────────────────────────────────────────────────────────
#> Mauchly's W p Greenhouse-Geisser ε Huynh-Feldt ε
#> ──────────────────────────────────────────────────────────────────────────────────
#> Messzeitpunkt 0.712 0.305 0.777 0.929
#> ──────────────────────────────────────────────────────────────────────────────────
A full-factorial model including all main effects and interactions is specified by combining the factors using the multiplication sign on the right-hand side of the formula:
factor_A*factor_B. This is equivalent tofactorA + factorB + factorA:factorB.