pacman::p_load(tidyverse, ggplot2, ggthemes, psych, haven, EFAutilities, knitr, lavaan, semPlot, psychTools)6 Konfirmatorische Faktorenanalyse (CFA)
6.1 Setup
Das Beispieldaten-Setup für die CFA ist identisch mit dem Setup der Kapitel zu PCA und EFA, bis auf eine kleine Änderung bei den Variablennamen.
Packages laden, Daten einlesen und aufbereiten:
# Daten einlesen
lifesat <- read_csv("https://github.com/methodenlehre/data/blob/master/statistik_IV/lifesat.csv?raw=true") Die Daten der Lebenszufriedenheit bestehen aus 10 Items, welche sich auf verschiedene Aspekte/Bereiche der Lebenszufriedenheit beziehen. Die Jugendlichen wurden gefragt:
“Wie zufrieden bist Du…”
| Fragen | |
|---|---|
| leben1 | mit deinen Schulnoten? |
| leben2 | mit deinem Aussehen und deiner Erscheinung? |
| leben3 | mit der Beziehung zu deinen Lehrern? |
| leben4 | mit allem, was mit der Schule zu tun hat? |
| leben5 | mit allem, was mit deiner Beziehung zu anderen Menschen zu tun hat? |
| leben6 | mit deiner Person? |
| leben7 | mit der Beziehung zu deinen Freunden? |
| leben8 | mit der Beziehung zu deinen Eltern? |
| leben9 | mit dem Zusammenleben mit den anderen Familienmitgliedern? |
| leben10 | mit dem Lebensstandard und dem Ansehen deiner Familie? |
Geantwortet wurde auf einer 7-stufigen Skala von 1 = “überhaupt nicht zufrieden” bis 7 = “sehr zufrieden”.
Die Fragen zur Lebenszufriedenheit können in vier Aspekte/Bereiche gegliedert werden:
Familie: Items 8, 9 und 10
Schule: Items 1, 3 und 4
Selbst: Items 2 und 6
Freunde: Items 7 und 5
Entsprechend ändern wir jetzt die Namen der Variablen, damit die Zuordnung etwas klarer wird. Um die Reihenfolge der Variablen mit ihrer inhaltlichen Ausrichtung in Übereinstimmung zu bringen, ändern wir die Reihenfolge noch mit select().
lifesat <- lifesat |>
rename(fam1 = leben8,
fam2 = leben9,
fam3 = leben10,
schule1 = leben1,
schule2 = leben3,
schule3 = leben4,
selbst1 = leben2,
selbst2 = leben6,
freund1 = leben5,
freund2 = leben7) |>
select(schule1, schule2, schule3,
selbst1, selbst2,
freund1, freund2,
fam1, fam2, fam3)summary(lifesat) schule1 schule2 schule3 selbst1
Min. :1.000 Min. :1.000 Min. :1.000 Min. :2.000
1st Qu.:4.000 1st Qu.:4.000 1st Qu.:4.000 1st Qu.:5.000
Median :5.000 Median :5.000 Median :5.000 Median :6.000
Mean :4.824 Mean :4.851 Mean :4.518 Mean :5.365
3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:5.000 3rd Qu.:6.000
Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
selbst2 freund1 freund2 fam1
Min. :3.000 Min. :3.000 Min. :4.000 Min. :2.000
1st Qu.:5.000 1st Qu.:5.000 1st Qu.:6.000 1st Qu.:5.000
Median :6.000 Median :6.000 Median :6.000 Median :6.000
Mean :5.812 Mean :5.671 Mean :6.243 Mean :6.004
3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:7.000 3rd Qu.:7.000
Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
fam2 fam3
Min. :2.000 Min. :3.000
1st Qu.:5.000 1st Qu.:5.000
Median :6.000 Median :6.000
Mean :5.796 Mean :5.949
3rd Qu.:6.000 3rd Qu.:7.000
Max. :7.000 Max. :7.000 6.2 lavaan
Lavaan ist ein kostenloses Open-Source-Paket für die latente Variablenmodellierung in R. Man kann Lavaan verwenden, um eine Vielzahl von statistischen Modellen zu schätzen. Zum Beispiel Pfadanalysen, Strukturgleichungsmodelle und eben auch konfirmatorische Faktorenanalysen (CFA).
Der Name lavaan kommt von latent variable analysis.
In dieser Übung beschränken wir uns vor allem auf die cfa()-Funktion von lavaan.
Die Berechnung einer CFA mit lavaan besteht aus zwei Schritten. Zuerst muss ein Modell definiert werden, dann kann das Modell mit der cfa()-Funktion geschätzt werden. Diese Funktion nimmt als Input unsere Daten und unsere Modelldefinition.
6.2.1 Modell definieren
Modelldefinitionen in lavaan folgen alle der selben Syntax.
In der Syntax sind gewisse Zeichen (Operatoren) vordefiniert und es werden auch bestimmte Voreinstellungen vorgenommen, die man ggf. überschreiben muss. Z.B. wird per default die Skalierung der latenten Variablen über die Fixierung (auf den Wert 1) des Ladungsparameters des jeweils ersten Indikators (manifeste Variable) für eine bestimmte latente Variable erreicht. Ausserdem müssen die Ladungsparameter des Modells nicht explizit definiert werden, genauso wenig wie die Varianzparameter der Residualvariablen der manifesten Variablen.
=~ bedeutet, dass die zu bildende latente Variable (hier z.B. Faktor1, Name frei wählbar) links von dem Operator durch alle Variablen rechts davon definiert wird. Die manifesten (gemessenen) Variablen auf der rechten Seite werden mit einem + separiert. Diese müssen im Datenframe vorhanden sein.
Ein Beispiel für sechs Items, welche durch zwei Faktoren (latente Variablen) erklärt werden:
bsp_model <- "
# Die Reihenfolge, mit der die Faktoren definiert werden, spielt keine Rolle.
Faktor1 =~ var1 + var2 + var3
Faktor2 =~ var4 + var5 + var6
# Die Reihenfolge der manifesten Variablen ist nur für die Fixierung einer Ladung
# pro Faktor von Bedeutung. Hier werden die Ladungen von `var1` und `var4` auf
# den Wert 1 fixiert.
# Zudem haben wir Kommentare im String, die von lavaan ignoriert werden.
"Eine weitere Voreinstellung ist, dass für alle latenten Variablen in einer CFA automatisch eine Faktor-Kovarianz spezifiziert wird. Der Operator für die Spezifikation einer Kovarianz ist ~~. D.h. wir könnten in diesem Beispiel auch noch eine weitere Zeile mit Faktor1 ~~ Faktor2 hinzufügen, ohne dass sich an der Modelldefinition etwas ändern würde.
6.2.2 Modell schätzen
Ein Modell kann mit folgender Syntax geschätzt werden: cfa(model = bsp_model, data = dataframe)
Die direkte Ausführung dieser Syntax ergibt allerdings nur einen sehr begrenzten Output, der nur die Anzahl der geschätzten Parameter, der Anzahl Beobachtungen sowie die Chi-Quadrat-Statistik enthält.
Daher muss das Ergebnis von cfa() zunächst in einem Output-Objekt (z.B. fit_bsp_model) abgespeichert und der ausführliche Output (mit den Parameterschätzern) mit summary(fit_bsp_model) extrahiert werden. Für die summary()-Funktion gibt es einige zusätzliche Argumente: fit.measures = TRUE gibt beispielsweise eine Reihe globaler Fitindizes (z.B. SRMR, RMSEA, CLI, TLI) sowie Informationskriterien (z.B. AIC und BIC) aus, und mit standardized = TRUE erhalten wir neben den unstandardisierten Parameterschätzern auch die standardisierten Parameterschätzer.
6.3 CFA zu Lebenszufriedenheitsbereichen
In diesem Kapitel fitten wir unterschiedlich komplexe CFA-Modelle auf unsere ls-Daten und vergleichen die Modelle anschliessend miteinander. Zunächst schauen wir uns theoriegeleitet ein 4-Faktor-Modell an, dann als Alternative dazu ein (sparsameres, da weniger Parameter schätzendes) 3-Faktor-Modell. In einem Vertiefungsteil schauen wir uns dann noch eine alternative Formulierung des 3-Faktor-Modells an, um zu zeigen, dass das 3-Faktor-Modell im 4-Faktor-Modell genestet ist (und damit ein Modellvergleich mittels LR-Test möglich ist). Die Modelle in diesem Kapitel sind Modelle mit Faktoren erster Ordnung. In Kapitel 6.3.4 betrachten wir dann noch ein Modell mit einem zusätzlichen Gesamt-Lebenszufriedenheitsfaktor zweiter Ordnung.
6.3.1 CFA mit vier Faktoren
Aus theoretischen Gründen schätzen wir zunächst ein Modell mit vier Faktoren. Für jeden inhaltlich definierten Lebenszufriedenheitsbereich (Schule, Selbst, Freunde, Familie) definieren wir einen Faktor. Ausserdem postulieren wir wie üblich eine Einfachstruktur, d.h. alle potentiellen Querladungen werden auf den Wert 0 restringiert (indem manifeste Variablen in der Modelldefinition nur in der Gleichung des zugehörigen Faktor auftauchen).
6.3.1.1 Modell definieren
model_4f <- "
# Der erste Faktor bezieht sich auf den Bereich `schule`
schule =~ schule1 + schule2 + schule3
# Der zweite Faktor bezieht sich auf den Bereich `selbst`
selbst =~ selbst1 + selbst2
# Der dritte Faktor bezieht sich auf den Bereich `freunde`
freunde =~ freund1 + freund2
# Der vierte Faktor bezieht sich auf den Bereich `familie`
familie =~ fam1 + fam2 + fam3
"Das Modell kann man sich folgendermassen vorstellen:
Typische Aufgabe: Schritt für Schritt
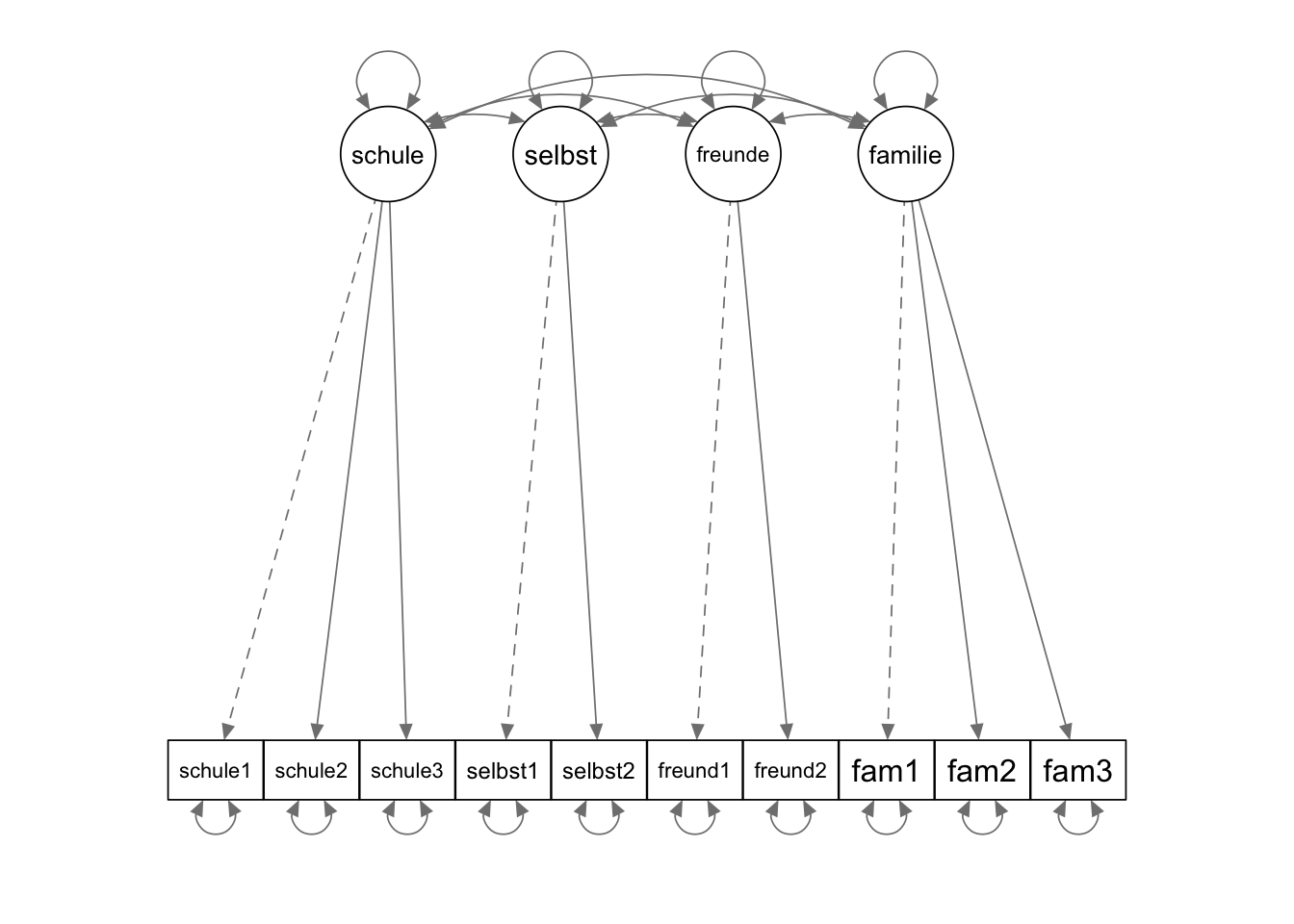
In diesem Abschnitt schauen wir uns zusammen die Struktur des CFA-Modells genauer an. Dabei hilft uns die obige Visualisierung des Modells. Fragen zur Struktur des Modells (e.g. Freiheitsgrade des Modells oder Anzahl latenter Variablen) eignen sich sehr gut, um das Verständnis von CFA-Modellen zu überprüfen.
Wie viele und welche manifeste Variablen hat das Modell?
10 manifeste Variablen: schule1, schule2, schule3, selbst1, selbst2, freund1, freund2, fam1, fam2, fam3
Wie viele Informationen \((n_{Info})\) enthält die Varianz-Kovarianz-Matrix der manifesten Variablen?
\(n_{Info} = \frac{p \cdot (p + 1)}{2} = \frac{10\cdot11}{2} = 55\)
Das könnte man auch ganz einfach zählen, wenn man sich die Varianz-Kovarianz Matrix der manifesten Variablen ansieht und dann die Einträge in dieser Matrix zählt.
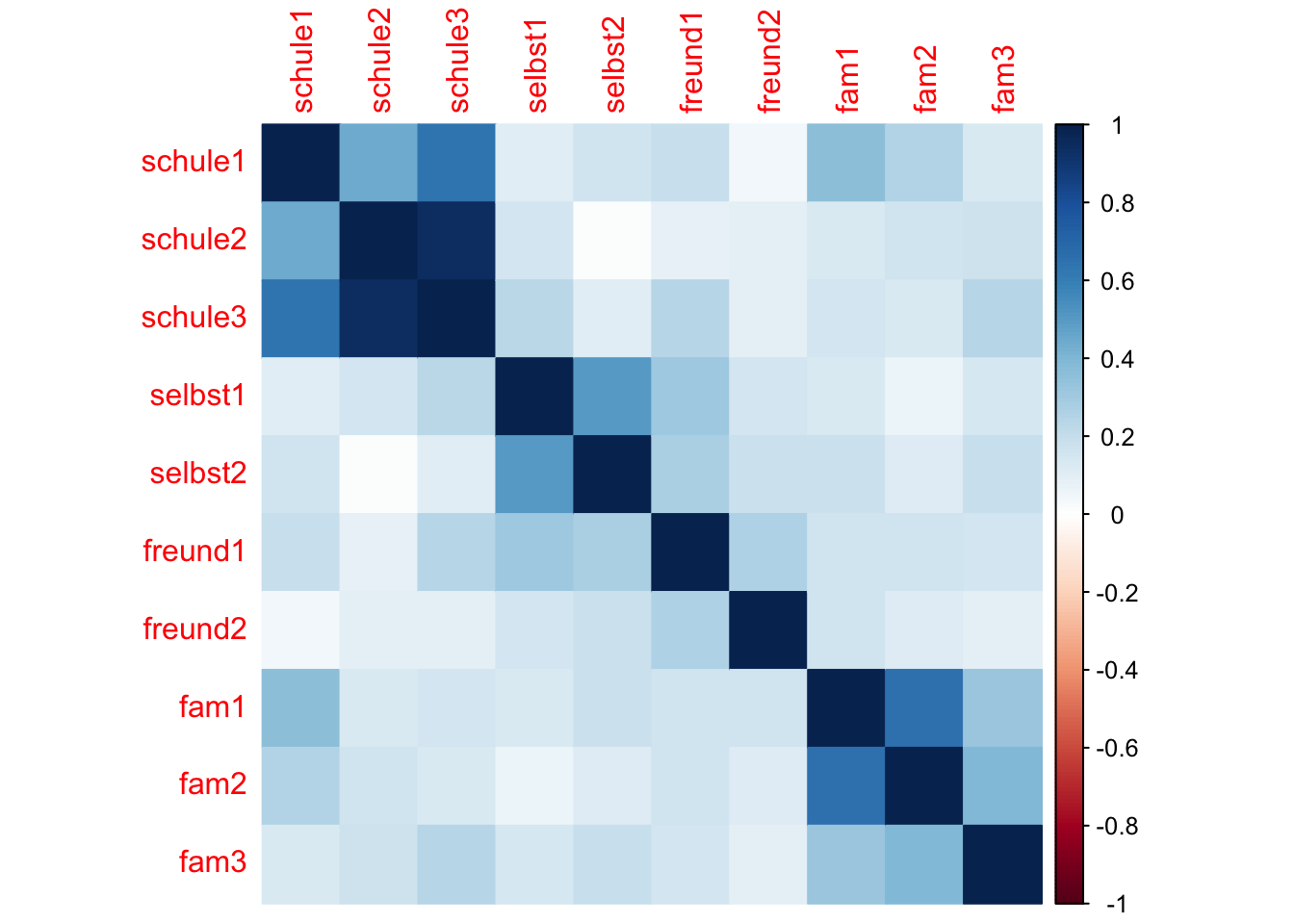
Beachte dabei, dass wie immer jeder Kovarianz-Wert doppelt vorkommt (die Matrix ist symmetrisch). Wir dürfen aber nur jeweils einen davon zählen. Hier zählen wir das untere Dreieck der Matrix (und die Diagonale, auf der sich die Varianz-Werte befinden).
schul1 schul2 schul3 slbst1 slbst2 frend1 frend2 fam1 fam2 fam3
schule1 1
schule2 2 11
schule3 3 12 20
selbst1 4 13 21 28
selbst2 5 14 22 29 35
freund1 6 15 23 30 36 41
freund2 7 16 24 31 37 42 46
fam1 8 17 25 32 38 43 47 50
fam2 9 18 26 33 39 44 48 51 53
fam3 10 19 27 34 40 45 49 52 54 55Wie viele und welche latenten Variablen hat das Modell?
14 latente Variablen: 4 Faktoren (familie, schule, selbst, freunde) und 10 Residualvariablen der manifesten Variablen (ohne Namen)
Wie viele und welche Parameter müssen geschätzt werden? \((n_{Par})\)
6 Faktorladungen
10 Varianzen der Residualvariablen der manifesten Variablen
4 Varianzen der latenten Faktoren
6 Kovarianzen zwischen den latenten Faktoren
\(n_{Par} = 6 + 10 + 4 + 6 = 26\)
Wie viele Freiheitsgrade besitzt das Modell?
\(df = n_{Info} - n_{Par} = 55 - 26 = 29\)
6.3.1.2 Modell schätzen
fit_mod4f <- cfa(model_4f, data = lifesat)
summary(fit_mod4f, fit.measures = TRUE, standardized = TRUE)lavaan 0.6-19 ended normally after 40 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 26
Number of observations 255
Model Test User Model:
Test statistic 51.433
Degrees of freedom 29
P-value (Chi-square) 0.006
Model Test Baseline Model:
Test statistic 583.039
Degrees of freedom 45
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.958
Tucker-Lewis Index (TLI) 0.935
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3427.760
Loglikelihood unrestricted model (H1) -3402.044
Akaike (AIC) 6907.520
Bayesian (BIC) 6999.593
Sample-size adjusted Bayesian (SABIC) 6917.166
Root Mean Square Error of Approximation:
RMSEA 0.055
90 Percent confidence interval - lower 0.029
90 Percent confidence interval - upper 0.079
P-value H_0: RMSEA <= 0.050 0.341
P-value H_0: RMSEA >= 0.080 0.045
Standardized Root Mean Square Residual:
SRMR 0.053
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
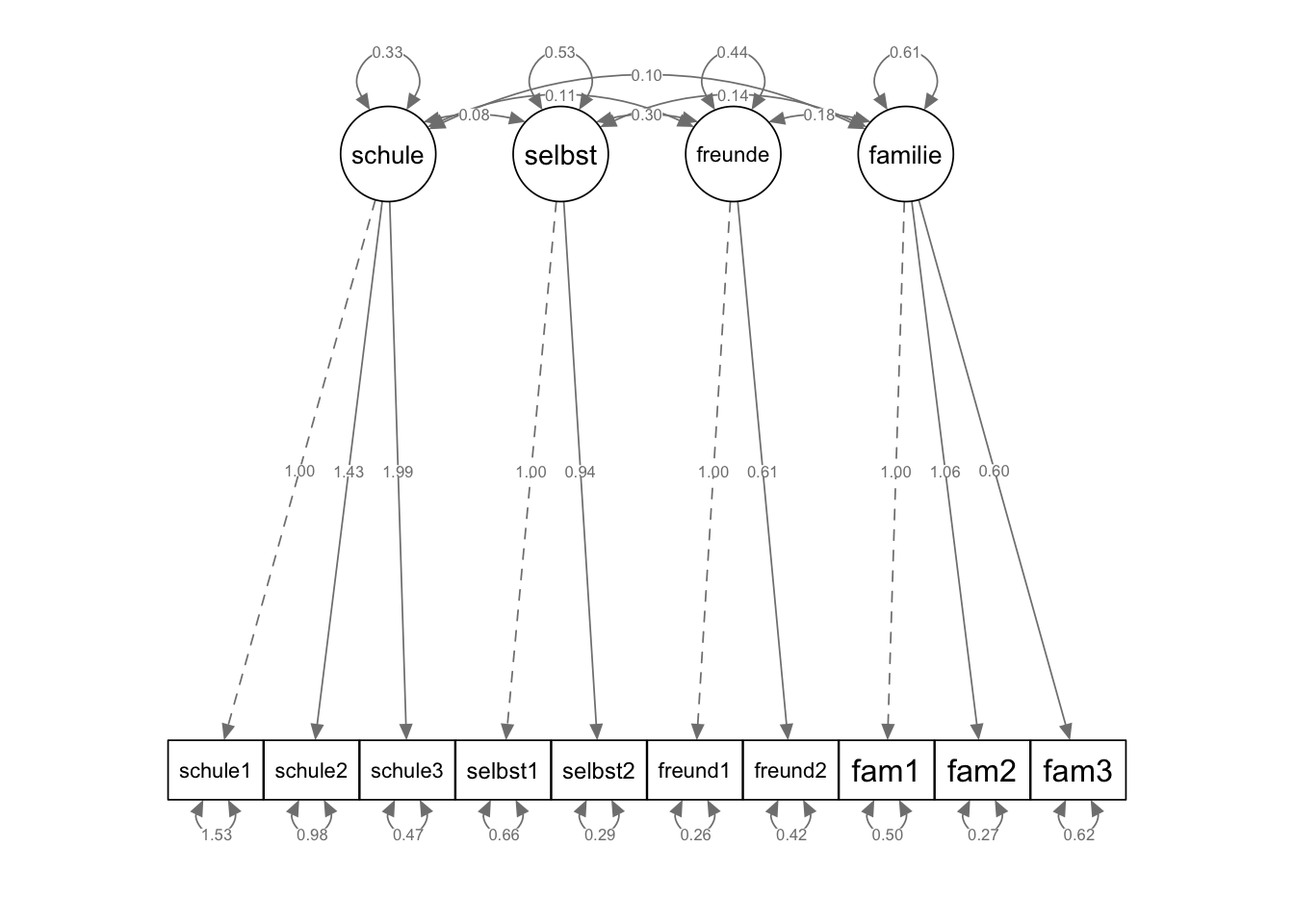
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
schule =~
schule1 1.000 0.572 0.420
schule2 1.431 0.257 5.572 0.000 0.819 0.638
schule3 1.995 0.403 4.947 0.000 1.141 0.858
selbst =~
selbst1 1.000 0.730 0.669
selbst2 0.940 0.156 6.028 0.000 0.685 0.784
freunde =~
freund1 1.000 0.661 0.791
freund2 0.614 0.117 5.235 0.000 0.406 0.531
familie =~
fam1 1.000 0.782 0.742
fam2 1.061 0.129 8.233 0.000 0.830 0.846
fam3 0.598 0.084 7.136 0.000 0.467 0.510
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
schule ~~
selbst 0.075 0.039 1.947 0.052 0.180 0.180
freunde 0.111 0.039 2.862 0.004 0.293 0.293
familie 0.098 0.040 2.427 0.015 0.219 0.219
selbst ~~
freunde 0.296 0.059 5.049 0.000 0.614 0.614
familie 0.142 0.052 2.735 0.006 0.249 0.249
freunde ~~
familie 0.178 0.048 3.700 0.000 0.344 0.344
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.schule1 1.528 0.147 10.414 0.000 1.528 0.824
.schule2 0.978 0.137 7.130 0.000 0.978 0.593
.schule3 0.469 0.209 2.245 0.025 0.469 0.265
.selbst1 0.656 0.100 6.575 0.000 0.656 0.552
.selbst2 0.295 0.076 3.865 0.000 0.295 0.386
.freund1 0.262 0.079 3.301 0.001 0.262 0.375
.freund2 0.419 0.047 8.948 0.000 0.419 0.718
.fam1 0.498 0.079 6.336 0.000 0.498 0.449
.fam2 0.274 0.077 3.574 0.000 0.274 0.285
.fam3 0.622 0.061 10.240 0.000 0.622 0.740
schule 0.327 0.109 3.001 0.003 1.000 1.000
selbst 0.532 0.120 4.452 0.000 1.000 1.000
freunde 0.437 0.095 4.594 0.000 1.000 1.000
familie 0.611 0.109 5.593 0.000 1.000 1.000\(~\)
Interpretation des Modells
Eine korrekte Interpretation des R Outputs ist ein wichtiger Bestandteil der Lernziele für die CFA.
Wie sehen die Faktorladungen aus? Sind alle signifikant?
Alle Faktorladungen sind signifikant (\(p < 0.001\)). Die standardisierten Ladungen (Std.all) schwanken zwischen 0.420 (schule =~ schule1) und 0.858 (schule =~ schule3).
Sind die Kovarianzen/Korrelationen zwischen den Faktoren signifikant?
Bis auf schule ~~ selbst (\(p = 0.052\)) sind alle Kovarianzen signifikant. Die stärkste Kovarianz/Korrelation findet sich mit 0.296/0.614 zwischen freunde ~~ selbst, also zwischen den beiden Faktoren, die in der EFA zusammen auf einem Faktor geladen haben.
Sind die Faktorvarianzen sowie Varianzen der Residualvariablen signifikant?
Ja, alle Residualvarianzen sind signifikant (\(p < 0.05\)).
Wie gross sind die Kommunalitäten der manifesten Variablen?
Die Kommunalitäten erhalten wir entweder über eine Quadrierung der zu einer manifesten Variablen gehörenden standardisierten Ladung oder über die Differenz 1 minus die standardisierte Residualvarianz (Uniqueness) einer manifesten Variablen.
Die höchste Kommunalität ist daher die von schule3 mit \(0.858^2 = 1 - 0.265 \approx 0.735\) und die niedrigste die von schule1 mit \(0.420^2 = 1 - 0.824 \approx 0.176\).
6.3.1.3 Modell visualisieren
Wir visualisieren Strukturgleichungsmodelle mit dem Package semPlot.
semPaths(fit_mod4f, "par",
weighted = FALSE, nCharNodes = 7, shapeMan = "rectangle",
sizeMan = 8, sizeMan2 = 5
)
6.3.1.4 Lokaler Fit: Vergleich der empirischen mit der vom Modell implizierten Varianz-Kovarianz-Matrix
Lokaler Fit bezieht sich auf die Frage, wie gut das Modell einzelne beobachtete Varianzen und Kovarianzen abbildet/repräsentiert. Wir vergleichen dafür die vom Modell implizierte Varianz-Kovarianz-Matrix mit der empirischen Varianz-Kovarianz-Matrix (der gemessenen Variablen).
Die Funktion lavInspect() aus dem Package lavaan ermöglicht die Extraktion von Informationen aus einem lavaan-Objekt. Mit dem Argument what spezifiziert man, welche Informationen extrahiert werden sollen. Der Wert sampstat dieses Arguments steht für “sample statistics”, also für die empirische Varianz-Kovarianz-Matrix:
lavInspect(fit_mod4f, what = "sampstat")$cov
schul1 schul2 schul3 slbst1 slbst2 frend1 frend2 fam1 fam2 fam3
schule1 1.855
schule2 0.444 1.648
schule3 0.640 0.944 1.771
selbst1 0.104 0.156 0.235 1.189
selbst2 0.167 0.015 0.105 0.500 0.765
freund1 0.193 0.088 0.249 0.312 0.271 0.699
freund2 0.043 0.095 0.098 0.151 0.183 0.268 0.584
fam1 0.369 0.134 0.159 0.136 0.189 0.170 0.168 1.110
fam2 0.258 0.162 0.137 0.067 0.118 0.164 0.116 0.656 0.962
fam3 0.136 0.173 0.242 0.144 0.198 0.160 0.099 0.326 0.394 0.841Die vom Modell implizierte Varianz-Kovarianz-Matrix erhält man mit what = 'implied':
lavInspect(fit_mod4f, what = "implied")$cov
schul1 schul2 schul3 slbst1 slbst2 frend1 frend2 fam1 fam2 fam3
schule1 1.855
schule2 0.468 1.648
schule3 0.653 0.934 1.771
selbst1 0.075 0.108 0.150 1.189
selbst2 0.071 0.101 0.141 0.500 0.765
freund1 0.111 0.159 0.221 0.296 0.278 0.699
freund2 0.068 0.097 0.136 0.182 0.171 0.268 0.584
fam1 0.098 0.140 0.196 0.142 0.134 0.178 0.109 1.110
fam2 0.104 0.149 0.208 0.151 0.142 0.189 0.116 0.649 0.962
fam3 0.059 0.084 0.117 0.085 0.080 0.106 0.065 0.365 0.388 0.841Je kleiner die Unterschiede zwischen diesen beiden Matrizen, desto besser passt das Modell auf die Daten, d.h. desto näher kommen die aus den geschätzten Parametern zurückgerechneten Varianzen und Kovarianzen an die empirischen Varianzen und Kovarianzen heran.
# Differenz der Matrizen berechnen und Ergebnis (Residualmatrix)
# in einem Objekt abspeichern
residualmatrix <-
lavInspect(fit_mod4f, what = "sampstat")$cov -
lavInspect(fit_mod4f, what = "implied")$cov
residualmatrix schul1 schul2 schul3 slbst1 slbst2 frend1 frend2 fam1 fam2 fam3
schule1 0.000
schule2 -0.024 0.000
schule3 -0.013 0.009 0.000
selbst1 0.028 0.049 0.085 0.000
selbst2 0.096 -0.086 -0.036 0.000 0.000
freund1 0.082 -0.070 0.028 0.016 -0.007 0.000
freund2 -0.025 -0.002 -0.038 -0.031 0.012 0.000 0.000
fam1 0.271 -0.007 -0.037 -0.006 0.055 -0.008 0.059 0.000
fam2 0.154 0.013 -0.071 -0.084 -0.023 -0.024 0.001 0.007 0.000
fam3 0.077 0.089 0.125 0.059 0.118 0.054 0.034 -0.040 0.006 0.000Eine direkte Extraktion der Residualmatrix ist mit dem Argument what = "resid" möglich:
residualmatrix2 <- lavInspect(fit_mod4f, what = "resid")$covUm das ganze in diesem Dokument nicht doppelt darzustellen, zeigen wir lediglich, dass der Inhalt der beiden Objekte residualmatrix und residualmatrix2 exakt gleich ist:
all.equal(residualmatrix, residualmatrix2)[1] TRUEFür die lokale Fit-Diagnose besonders relevant ist die Varianz-Kovarianz-Matrix der standardisierten Residuen. Diese extrahieren wir nicht mit lavInspect(), sondern direkt mit resid().
resid(fit_mod4f, type = "standardized")$cov schul1 schul2 schul3 slbst1 slbst2 frend1 frend2 fam1 fam2 fam3
schule1 0.000
schule2 -0.640 0.000
schule3 -1.035 2.314 0.000
selbst1 0.336 0.698 1.529 0.000
selbst2 1.437 -1.738 -1.196 0.000 0.000
freund1 1.331 -1.659 1.254 1.235 -0.901 0.000
freund2 -0.421 -0.044 -0.843 -1.100 0.680 0.000 0.000
fam1 3.298 -0.106 -0.764 -0.126 1.645 -0.266 1.560 0.000
fam2 2.081 0.243 -2.382 -2.080 -1.010 -1.338 0.017 2.679 0.000
fam3 1.064 1.357 1.960 1.080 2.829 1.386 0.892 -2.809 0.790 0.000\(~\)
Interpretation der Residuen
Betrachten Sie die Sample-(Ko-)Varianzmatrix und die Implizierte (Ko-)Varianzmatrix. Welches sind die drei stärksten Abweichungen zwischen beiden Matrizen? Werden die ensprechenden Varianzen/Kovarianzen vom Modell unter- oder überschätzt?
Dazu betrachten wir die unstandardisierte Residualmatrix.
fam1 ~~ schule1 = 0.271
fam2 ~~ schule1 = 0.154
fam3 ~~ schule3 = 0.125
Bei den drei grössten Abweichungen sind die empirischen Kovarianzen grösser als die vom Modell implizierten. Sie werden also durch das Modell unterschätzt, daher sind die zugehörigen Residualkovarianzen alle positiv. Inhaltlich erklärbar sind diese Abweichungen dadurch, dass im Modell keine Querladungen zugelassen sind, also z.B. Item schule1 (Schulnoten) nicht auf dem Familien-Faktor laden „darf”.
Welche sind signifikant?
Dazu benötigen wir die standardisierte Residualmatrix. Dort schauen wir, welche Werte (absolut) grösser sind als unsere z-verteilte Prüfgrösse \((\geq 2,58\: \widehat=\: p\leq 0.01)\).
Nämlich:
fam1 ~~ schule1 = 3.298
fam3 ~~ selbst2 = 2.829
fam3 ~~ fam1 = -2.809
fam2 ~~ fam1 = 2.679
Interessanterweise beziehen sich zwei der vier signifikanten Residualkovarianzen auf solche innerhalb des Familien-Faktors!
6.3.1.5 Globaler Fit
\(CFI = 0.958\) und \(NNFI/TLI = 0.935\) (siehe Output unter 3.2) nehmen Werte knapp unter empfohlenen Cut-Off-Kriterien für einen guten Fit von 0.97 bzw. 0.95 an.
Der \(RMSEA = 0.055\) liegt zwar knapp über dem Cut-Off für einen guten Model Fit von 0.05, ist aber nicht signifikant \((p = 0.341)\) grösser als dieser, und gleichzeitig signifikant kleiner als der Cut-off von 0.08, ab dem der Model Fit als schlecht gilt \((p = 0.045)\). Das 90 %-CI des RMSEA von \([0.029; 0.079]\) beinhaltet dementsprechend den Wert 0.05, nicht aber den Wert 0.08.
Auch nach dem \(SRMR = 0.053\) ist der Model Fit als gut (< 0.08) zu beurteilen.
\(~\)
CFI und NNFI/TLI sowie die Informationskriterien AIC und BIC von Hand berechnet
Wie in der Vorlesung erwähnt, sind diese Formeln prüfungsrelevant.
\(\begin{aligned} CFI &= 1-\frac{\chi_{t}^{2}-d f_{t}}{\chi_{i}^{2}-d f_{i}}\\ &= 1-\frac{51.433-29}{583.039 -45}\\ &= 1-\frac{22.433}{538.039}\\ &= 0.958 \end{aligned}\)
\(~\)
\(\begin{aligned} NNFI/TLI &= \left(\frac{\chi_{i}^{2}}{d f_{i}}-\frac{\chi_{t}^{2}}{d f_{t}}\right)/\left({\frac{\chi_{i}^{2}}{d f_{i}}-1}\right) \\ &= \left(\frac{583.039}{45}-\frac{51.433}{29}\right)/\left({\frac{583.039}{45}-1}\right) \\ &= \frac{12.956-1.774}{12.956-1} \\ &= 0.935 \end{aligned}\)
\(~\)
\(\begin{aligned} AIC &=\chi^{2}+2 \cdot t\\ &= 51.433+ 2 \cdot 26 \\ &= 103.433 \end{aligned}\)
\(~\)
\(\begin{aligned} BIC &=\chi^{2}+ \ln (n) \cdot t \\ &=51.433 + 26 \cdot \ln (255)\\ &=51.433+26 \cdot 5.541\\ &= 195.499 \end{aligned}\)
\(~\)
AIC und BIC unterscheiden sich von den von lavaan berechneten Werten, da letztere auf Basis der -2 Log-Likelihood und nicht auf der Basis von Chi-Quadrat berechnet werden. Für Modellvergleiche (s.u.) spielt es aber keine Rolle, welche dieser beiden Model-Fit-Statistiken man als Ausgangspunkt für die Berechnung von AIC und BIC nimmt. Da sich Chi-Quadrat und -2 Log-Likelihood nur um eine zu vernachlässigende Konstante voneinander unterscheiden, weist z.B. der AIC zweier Modelle immer dieselbe Differenz unabhängig von der Berechnungsart auf.
6.3.2 CFA mit drei Faktoren
6.3.2.1 Modell definieren
Wir definieren hier ein Modell mit drei Faktoren, da wir bei der EFA gesehen haben, dass ein solches möglicherweise ein sparsameres Alternativmodell sein könnte.
model_3f <- "
# Der erste Faktor ist `schule`
schule =~ schule1 + schule2 + schule3
# Als zweiten Faktor kombinieren wir jetzt `selbst` und `freunde`
selbstfreunde =~ selbst1 + selbst2 + freund1 + freund2
# Zum Schluss die `familie`
familie =~ fam1 + fam2 + fam3
"6.3.2.2 Modell schätzen
fit_mod3f <- cfa(model_3f, data = lifesat)
summary(fit_mod3f, fit.measures = TRUE, standardized = TRUE)lavaan 0.6-19 ended normally after 39 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 23
Number of observations 255
Model Test User Model:
Test statistic 79.522
Degrees of freedom 32
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 583.039
Degrees of freedom 45
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.912
Tucker-Lewis Index (TLI) 0.876
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3441.804
Loglikelihood unrestricted model (H1) -3402.044
Akaike (AIC) 6929.609
Bayesian (BIC) 7011.058
Sample-size adjusted Bayesian (SABIC) 6938.142
Root Mean Square Error of Approximation:
RMSEA 0.076
90 Percent confidence interval - lower 0.055
90 Percent confidence interval - upper 0.098
P-value H_0: RMSEA <= 0.050 0.021
P-value H_0: RMSEA >= 0.080 0.408
Standardized Root Mean Square Residual:
SRMR 0.064
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
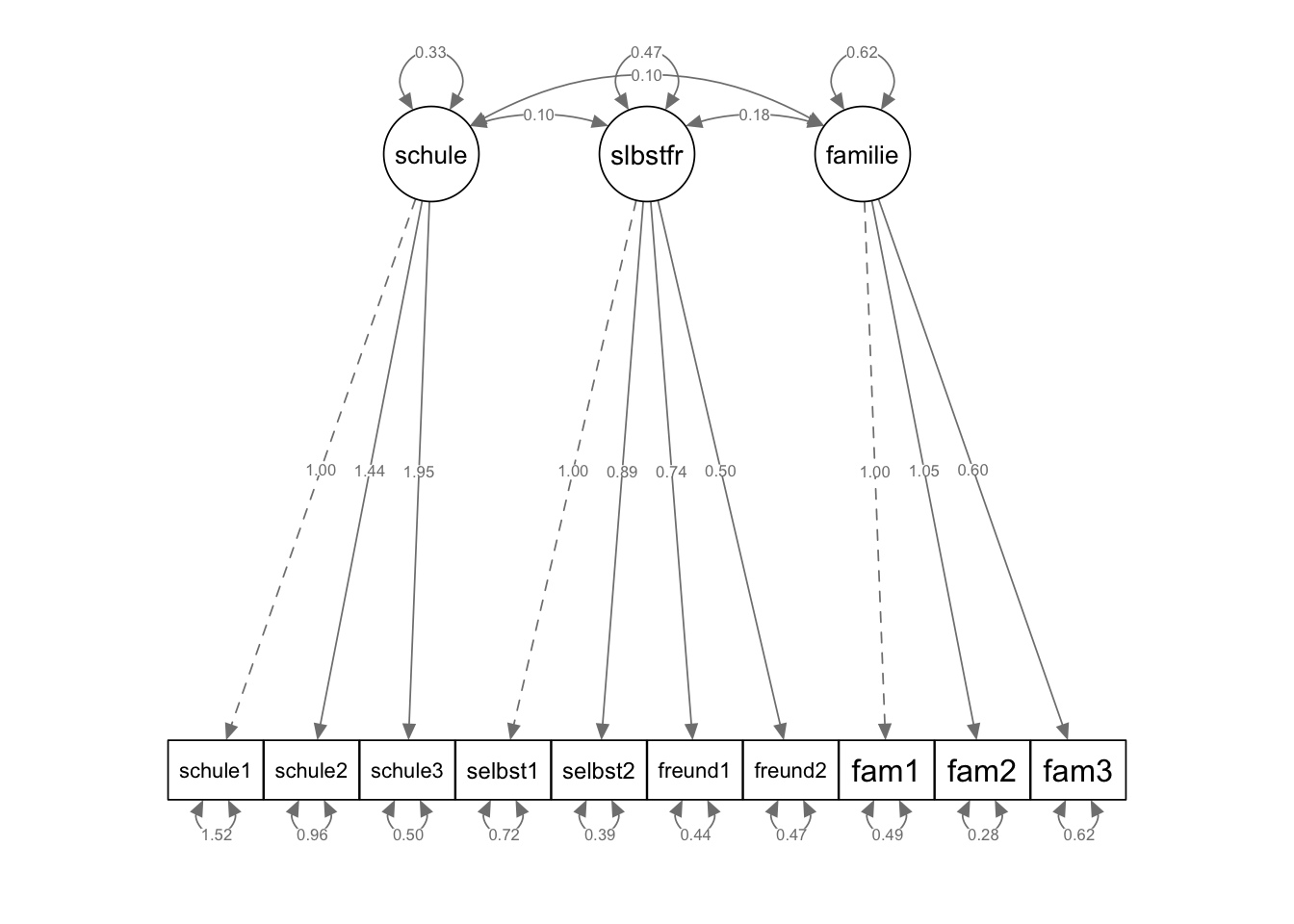
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
schule =~
schule1 1.000 0.577 0.424
schule2 1.436 0.258 5.574 0.000 0.828 0.645
schule3 1.954 0.393 4.971 0.000 1.127 0.847
selbstfreunde =~
selbst1 1.000 0.686 0.629
selbst2 0.889 0.127 7.006 0.000 0.610 0.698
freund1 0.741 0.110 6.722 0.000 0.509 0.608
freund2 0.502 0.092 5.465 0.000 0.344 0.450
familie =~
fam1 1.000 0.787 0.747
fam2 1.048 0.128 8.191 0.000 0.824 0.840
fam3 0.596 0.084 7.131 0.000 0.469 0.511
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
schule ~~
selbstfreunde 0.103 0.039 2.616 0.009 0.261 0.261
familie 0.102 0.041 2.468 0.014 0.225 0.225
selbstfreunde ~~
familie 0.178 0.051 3.507 0.000 0.331 0.331
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.schule1 1.522 0.147 10.379 0.000 1.522 0.821
.schule2 0.962 0.139 6.926 0.000 0.962 0.584
.schule3 0.501 0.206 2.429 0.015 0.501 0.283
.selbst1 0.718 0.087 8.236 0.000 0.718 0.604
.selbst2 0.393 0.057 6.907 0.000 0.393 0.513
.freund1 0.441 0.051 8.572 0.000 0.441 0.630
.freund2 0.466 0.046 10.154 0.000 0.466 0.797
.fam1 0.491 0.079 6.189 0.000 0.491 0.443
.fam2 0.283 0.077 3.700 0.000 0.283 0.295
.fam3 0.621 0.061 10.222 0.000 0.621 0.739
schule 0.333 0.110 3.019 0.003 1.000 1.000
selbstfreunde 0.470 0.103 4.571 0.000 1.000 1.000
familie 0.619 0.110 5.607 0.000 1.000 1.0006.3.2.3 Modell visualisieren
semPaths(fit_mod3f, "par",
weighted = FALSE, nCharNodes = 7, shapeMan = "rectangle",
sizeMan = 8, sizeMan2 = 5
)
\(~\)
Und jetzt mit standardisierten Parameterschätzern:
semPaths(fit_mod3f, "std",
weighted = FALSE, nCharNodes = 7, shapeMan = "rectangle",
sizeMan = 8, sizeMan2 = 5
)
6.3.2.4 Globaler Fit
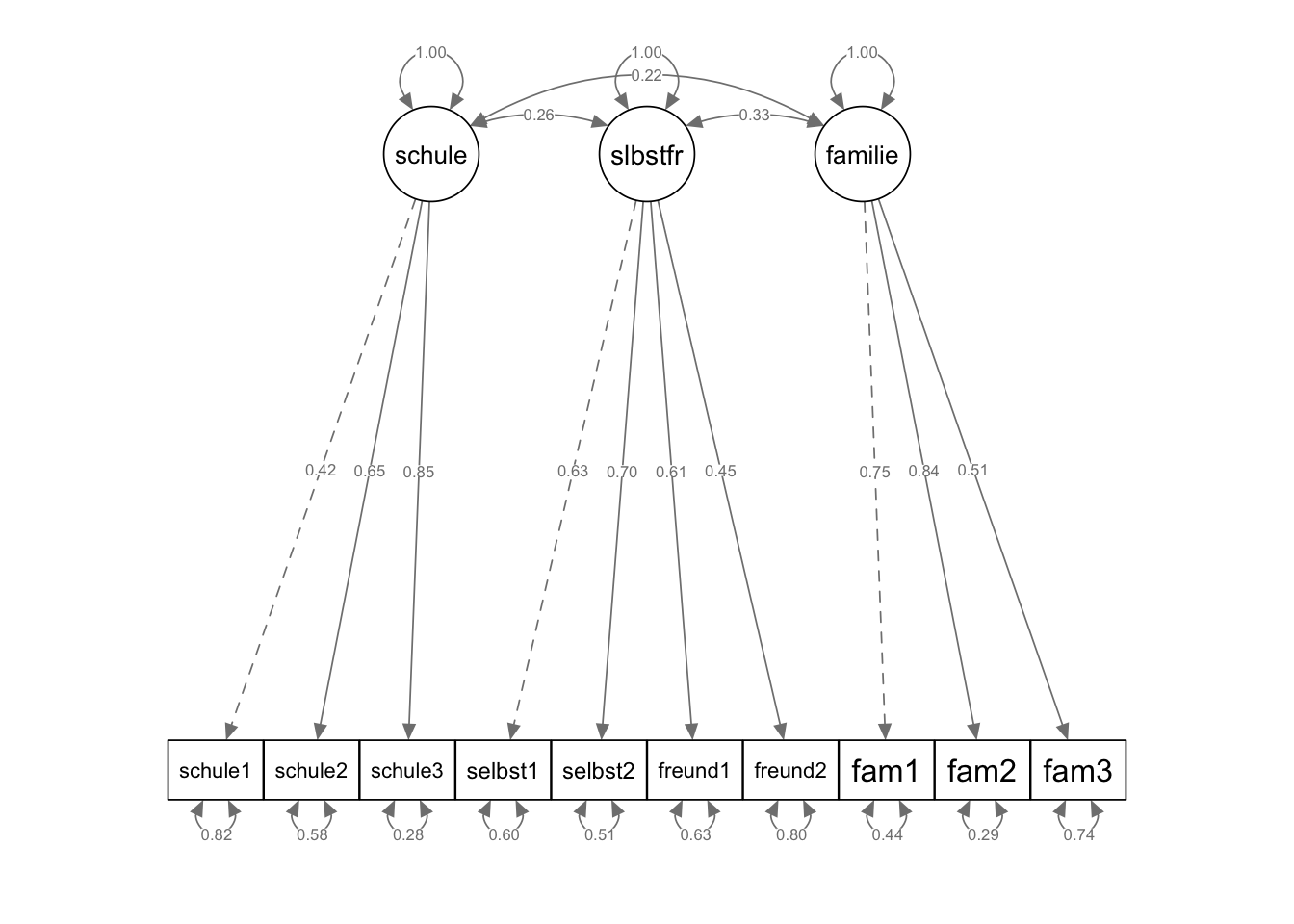
\(CFI = 0.912\) und \(NNFI/TLI = 0.876\) sind jetzt deutlich niedriger als die empfohlenen Cut-Off-Kriterien.
Der \(RMSEA = 0.076\) ist jetzt auch signifikant grösser als der Cut-Off von 0.05 \((p = 0.021)\) und nicht mehr signifikant kleiner als 0.08 \((p = 0.408)\). Das 90 %-CI des RMSEA von \([0.055; 0.098]\) beinhaltet dementsprechend den Wert 0.05 nicht, den Wert 0.08 aber schon.
Lediglich nach dem \(SRMR = 0.064\) ist der Model Fit noch als gut (< 0.08) zu beurteilen.
CFI und NNFI/TLI sowie die Informationskriterien AIC und BIC von Hand berechnet
\(\begin{aligned} CFI &= 1-\frac{\chi_{t}^{2}-d f_{t}}{\chi_{i}^{2}-d f_{i}}\\ &= 1-\frac{79.522-32}{583.039 -45}\\ &=1-\frac{47.522}{538.039}\\ &=0.912 \end{aligned}\)
\(~\)
\(\begin{aligned} NNFI/TLI &= \left(\frac{\chi_{i}^{2}}{d f_{i}}-\frac{\chi_{t}^{2}}{d f_{t}}\right)/\left({\frac{\chi_{i}^{2}}{d f_{i}}-1}\right) \\ &= \left(\frac{583.039}{45}-\frac{79.522}{32}\right)/\left({\frac{583.039}{45}-1}\right) \\ &= \frac{12.956-2.485}{12.956-1} \\ &= 0.876 \end{aligned}\)
\(~\)
\(\begin{aligned} AIC &= \chi^{2}+2 \cdot t\\ &= 79.522+ 2 \cdot 23 \\ &= 125.522 \end{aligned}\)
\(~\)
\(\begin{aligned} BIC &= \chi^{2}+t \cdot \ln (n)\\ &=79.522 + 23 \cdot \ln (255)=79.522+23 \cdot 5.541\\ &= 206.965 \end{aligned}\)
\(~\)
Vertiefung: Alternative Spezifikation des 3-Faktor-Modells
Ein 3-Faktor-Modell ist alternativ spezifizierbar, indem bestimmte Parameter des 4-Faktor-Modells restringiert werden. Damit können wir zeigen, dass das 3-Faktor-Modell im 4-Faktor-Modell genestet ist.
Um aus dem 4-Faktor-Modell ein 3-Faktor-Modell mit einem kombinierten Selbst- und Freunde-Faktor zu machen, muss durch Parameterrestriktionen dafür gesorgt werden, dass die Faktoren freunde und selbst sich wie ein einziger Faktor verhalten. Damit diese zwei Faktoren zu einem werden, muss zum einen die Kovarianz zwischen den beiden Faktoren auf den Wert 1 gesetzt werden (Syntax siehe unten). Damit eine Kovarianz von 1 wirklich eine exakte Gleichheit der beiden Faktoren bedeutet, müssen auch die Varianzen der beiden latenten Variablen gleich 1 sein (damit wird dann auch die Korrelation zwischen den latenten Variablen 1). Die einfachste Möglichkeit, um das zu erreichen, ist die Festlegung der Varianzen aller latenten Variablen auf den Wert 1 mit dem cfa()-Argument std.lv = TRUE, das gleichzeitg dafür sorgt, dass auch die Ladungen der ersten manifesten Variablen jedes Faktors frei geschätzt werden. Dieser Aspekt wird also nicht in der Modelldefinition, sondern erst bei der Modellschätzung festgelegt!
Zum anderen müssen die Zusammenhänge der Faktoren mit allen anderen Faktoren für beide Faktoren (freunde und selbst) identisch sein. Dies können wir erreichen, indem wir die Parameter der Faktoren-Kovarianzen benennen (d.h. explizit spezifizieren) und gleichzeitig den beiden gleichzusetzenden Parametern denselben Namen geben. Z.B. soll die Kovarianz von freunde und schule genau gleich geschätzt werden wie die Kovarianz zwischen selbst und schule. Wenn wir beide zu schätzende Parameter mit a benennen, erkennt lavaan, dass für beide Kovarianzen derselbe Wert geschätzt werden soll.
Dieses Modell nennen wir model_4f_res.
Modell definieren
model_4f_res <- "
schule =~ schule1 + schule2 + schule3
selbst =~ selbst1 + selbst2
freunde =~ freund1 + freund2
familie =~ fam1 + fam2 + fam3
# Restriktion Kovarianz
freunde ~~ 1 * selbst
# Gleichheitsrestriktionen: Kovarianzen mit gleichbenannten Parametern
freunde ~~ a * schule
selbst ~~ a * schule
freunde ~~ b * familie
selbst ~~ b * familie
"Modell schätzen
fit_mod4f_res <- cfa(model_4f_res, std.lv = TRUE, data = lifesat)
summary(fit_mod4f_res, fit.measures = TRUE, standardized = TRUE)lavaan 0.6-19 ended normally after 26 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 25
Number of equality constraints 2
Number of observations 255
Model Test User Model:
Test statistic 79.522
Degrees of freedom 32
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 583.039
Degrees of freedom 45
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.912
Tucker-Lewis Index (TLI) 0.876
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3441.804
Loglikelihood unrestricted model (H1) -3402.044
Akaike (AIC) 6929.609
Bayesian (BIC) 7011.058
Sample-size adjusted Bayesian (SABIC) 6938.142
Root Mean Square Error of Approximation:
RMSEA 0.076
90 Percent confidence interval - lower 0.055
90 Percent confidence interval - upper 0.098
P-value H_0: RMSEA <= 0.050 0.021
P-value H_0: RMSEA >= 0.080 0.408
Standardized Root Mean Square Residual:
SRMR 0.064
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
schule =~
schule1 0.577 0.096 6.037 0.000 0.577 0.424
schule2 0.828 0.097 8.499 0.000 0.828 0.645
schule3 1.127 0.111 10.109 0.000 1.127 0.847
selbst =~
selbst1 0.686 0.075 9.141 0.000 0.686 0.629
selbst2 0.610 0.060 10.126 0.000 0.610 0.698
freunde =~
freund1 0.509 0.058 8.829 0.000 0.509 0.608
freund2 0.344 0.054 6.378 0.000 0.344 0.450
familie =~
fam1 0.787 0.070 11.214 0.000 0.787 0.747
fam2 0.824 0.066 12.461 0.000 0.824 0.840
fam3 0.469 0.060 7.783 0.000 0.469 0.511
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
selbst ~~
freunde 1.000 1.000 1.000
schule ~~
freunde (a) 0.261 0.081 3.216 0.001 0.261 0.261
selbst (a) 0.261 0.081 3.216 0.001 0.261 0.261
freunde ~~
familie (b) 0.331 0.077 4.304 0.000 0.331 0.331
selbst ~~
familie (b) 0.331 0.077 4.304 0.000 0.331 0.331
schule ~~
familie 0.225 0.077 2.922 0.003 0.225 0.225
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.schule1 1.522 0.147 10.379 0.000 1.522 0.821
.schule2 0.962 0.139 6.926 0.000 0.962 0.584
.schule3 0.501 0.206 2.429 0.015 0.501 0.283
.selbst1 0.718 0.087 8.236 0.000 0.718 0.604
.selbst2 0.393 0.057 6.907 0.000 0.393 0.513
.freund1 0.441 0.051 8.572 0.000 0.441 0.630
.freund2 0.466 0.046 10.154 0.000 0.466 0.797
.fam1 0.491 0.079 6.189 0.000 0.491 0.443
.fam2 0.283 0.077 3.700 0.000 0.283 0.295
.fam3 0.621 0.061 10.222 0.000 0.621 0.739
schule 1.000 1.000 1.000
selbst 1.000 1.000 1.000
freunde 1.000 1.000 1.000
familie 1.000 1.000 1.000Modell visualisieren
Mit standardisierten Parameterschätzern:
semPaths(fit_mod4f_res, "std", "par",
weighted = FALSE, nCharNodes = 7,
shapeMan = "rectangle", sizeMan = 8, sizeMan2 = 5
)
Um bei allen Parametern exakt die gleichen standardisierten Parameterschätzer zu erhalten wie im “normal” definierten 3-Faktor-Modell oben, muss letzteres auch mit der Option std.lv = TRUE geschätzt werden. Sonst ergeben sich hier aufgrund der unterschiedlichen Festlegung der Skalierung der latenten Variablen kleine Unterschiede bei den Ladungen und bei den Residualvarianzen.
fit_mod3f_alt <- cfa(model_3f, std.lv = TRUE, data = lifesat)
semPaths(fit_mod3f_alt, "std", "par",
weighted = FALSE, nCharNodes = 7,
shapeMan = "rectangle", sizeMan = 8, sizeMan2 = 5
)
Modellvergleich von 3-Faktor-Modell und alternativem 3-Faktor-Modell
Ein Modellvergleich sollte jetzt zeigen, dass das 3-Faktor-Modell und das restringierte 4-Faktor-Modell gleich gut fitten, weil sie identisch sind.
Wir testen das:
anova(fit_mod3f, fit_mod4f_res)
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_mod3f 32 6929.6 7011.1 79.522
fit_mod4f_res 32 6929.6 7011.1 79.522 2.2919e-10 0 0 Das ist der Fall! (Die sehr kleine Zahl bei Chisq diff kommt durch minimale numerische Ungenauigkeiten bei der ML-Schätzung zu Stande.)
6.3.3 Modellvergleich 3-Faktor-Modell und 4-Faktor-Modell
Ausserdem wollen wir noch das 3-Faktor-Modell gegen das ursprüngliche 4-Faktormodell testen.
Dieser Test überprüft, ob die Nullhypothese, dass das 3-Faktor-Modell nicht schlechter als das 4-Faktor-Modell auf die Daten passt, aufrechterhalten werden kann oder abgelehnt werden muss.
anova(fit_mod3f, fit_mod4f)
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_mod4f 29 6907.5 6999.6 51.433
fit_mod3f 32 6929.6 7011.1 79.522 28.089 0.1811 3 3.479e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Vergleich ist signifikant. Das 3-Faktormodell passt also signifikant schlechter auf die Daten als das 4-Faktor-Modell.
Diese Schlussfolgerung ergibt sich auch aufgrund der oben bereits von Hand berechneten Informationskriterien AIC und BIC:
Beim AIC ergab sich für das 4-Faktor-Modell ein Wert von 103.433 und für das 3-Faktor-Modell ein Wert von 125.522 (respektive die von lavaan ausgegebenen AIC-Werte von 6907.52 und 6929.609). Nach dem AIC ist also das 4-Faktor-Modell zu bevorzugen (kleinerer AIC).
Beim BIC ergibt sich ein ähnliches Bild: von Hand gerechnet beim 4-Faktor-Modell BIC = 195.499 und beim 3-Faktor-Modell BIC = 206.965 (von lavaan ausgegebene Werte: 6999.593 und 7011.058). Auch nach dem (im Vergleich zum AIC) eher sparsamere Modelle (mit weniger Parametern) bevorzugenden BIC sollte also das 4-Faktor-Modell ausgewählt werden.
6.3.4 Modell mit Lebenszufriedenheitsfaktor zweiter Ordnung
Wie wir sehen können, sind die vier Faktoren im 4-Faktor-Modell alle positiv untereinander korreliert und diese Korrelationen sind mit einer Ausnahme \((r_{SchuleSelbst}=0.18, \; p = 0.052)\) auch signifikant. Dies und die Tatsache, dass die Lebenszufriedenheit in der psychologischen Forschung nicht nur bereichsspezifisch, sondern auch (und sogar vorwiegend) global konzeptualisiert wird, lassen vermuten, dass ein übergeordneter Faktor (higher order factor, 2nd order factor) Lebenszufriedenheit existiert, der die Korrelationen der bereichsspezifischen Lebenszufriedenheitsfaktoren erklären kann.
In der CFA können wir einen solchen Faktor zweiter Ordnung modellieren. Ein weiterer Faktor scheint das Modell zunächst komplizierter zu machen, doch das kann täuschen: Tatsächlich werden in einem Modell mit einem übergeordneten Faktor insgesamt zwei Parameter weniger geschätzt als im Modell mit vier Faktoren: Anstelle von sechs Kovarianzen zwischen den Faktoren werden jetzt vier Ladungen (bzw. drei Ladungen und eine Varianz des Faktors zweiter Ordnung) geschätzt.
6.3.4.1 Modell definieren
model_4f_2order <- "
schule =~ schule1 + schule2 + schule3
selbst =~ selbst1 + selbst2
freunde =~ freund1 + freund2
familie =~ fam1 + fam2 + fam3
# Übergeordneter Faktor Zufriedenheit
zufriedenheit =~ schule + selbst + freunde + familie
"6.3.4.2 Modell schätzen
fit_mod4f_2order <- cfa(model_4f_2order, lifesat)
summary(fit_mod4f_2order, fit.measures = TRUE, standardized = TRUE)lavaan 0.6-19 ended normally after 67 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of observations 255
Model Test User Model:
Test statistic 53.372
Degrees of freedom 31
P-value (Chi-square) 0.008
Model Test Baseline Model:
Test statistic 583.039
Degrees of freedom 45
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.958
Tucker-Lewis Index (TLI) 0.940
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3428.730
Loglikelihood unrestricted model (H1) -3402.044
Akaike (AIC) 6905.459
Bayesian (BIC) 6990.450
Sample-size adjusted Bayesian (SABIC) 6914.364
Root Mean Square Error of Approximation:
RMSEA 0.053
90 Percent confidence interval - lower 0.027
90 Percent confidence interval - upper 0.077
P-value H_0: RMSEA <= 0.050 0.387
P-value H_0: RMSEA >= 0.080 0.030
Standardized Root Mean Square Residual:
SRMR 0.060
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
schule =~
schule1 1.000 0.555 0.407
schule2 1.439 0.261 5.508 0.000 0.799 0.622
schule3 2.118 0.449 4.713 0.000 1.175 0.883
selbst =~
selbst1 1.000 0.736 0.675
selbst2 0.924 0.153 6.040 0.000 0.680 0.777
freunde =~
freund1 1.000 0.662 0.792
freund2 0.612 0.117 5.229 0.000 0.405 0.530
familie =~
fam1 1.000 0.780 0.741
fam2 1.068 0.131 8.136 0.000 0.833 0.849
fam3 0.595 0.084 7.106 0.000 0.465 0.507
zufriedenheit =~
schule 1.000 0.322 0.322
selbst 2.720 0.985 2.763 0.006 0.661 0.661
freunde 3.397 1.250 2.717 0.007 0.917 0.917
familie 1.686 0.661 2.550 0.011 0.386 0.386
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.schule1 1.547 0.148 10.481 0.000 1.547 0.834
.schule2 1.011 0.139 7.278 0.000 1.011 0.613
.schule3 0.390 0.231 1.689 0.091 0.390 0.220
.selbst1 0.647 0.100 6.442 0.000 0.647 0.544
.selbst2 0.303 0.075 4.020 0.000 0.303 0.396
.freund1 0.261 0.080 3.277 0.001 0.261 0.373
.freund2 0.420 0.047 8.958 0.000 0.420 0.719
.fam1 0.501 0.079 6.317 0.000 0.501 0.452
.fam2 0.268 0.078 3.429 0.001 0.268 0.279
.fam3 0.625 0.061 10.256 0.000 0.625 0.743
.schule 0.276 0.095 2.915 0.004 0.896 0.896
.selbst 0.305 0.091 3.369 0.001 0.563 0.563
.freunde 0.070 0.106 0.661 0.509 0.159 0.159
.familie 0.518 0.097 5.360 0.000 0.851 0.851
zufriedenheit 0.032 0.021 1.536 0.125 1.000 1.0006.3.4.3 Modell visualisieren
Hier jetzt gleich mit standardisierten Parametern:
semPaths(fit_mod4f_2order, "std",
weighted = FALSE, nCharNodes = 7,
shapeMan = "rectangle", sizeMan = 8, sizeMan2 = 5
)
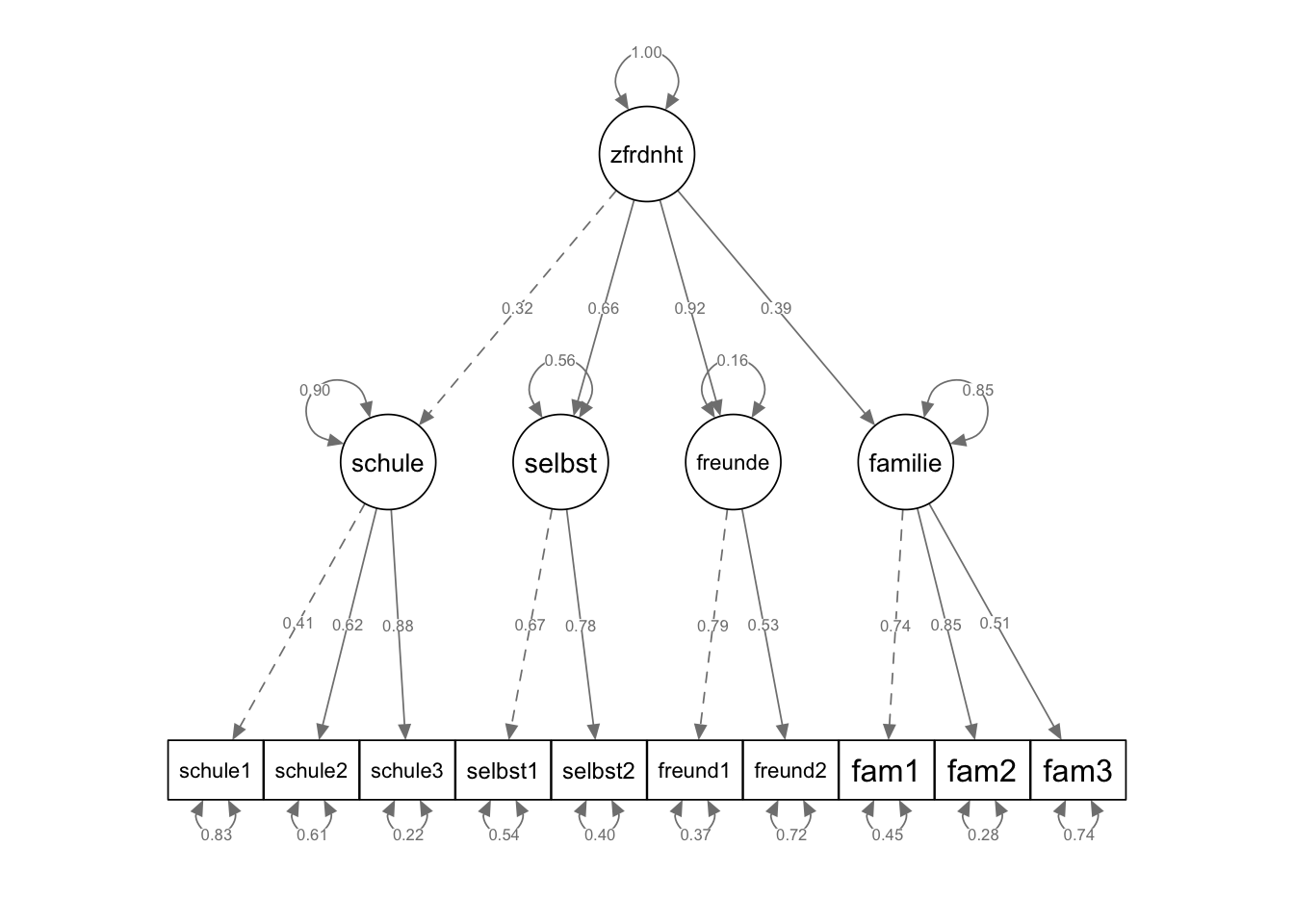
Die Parameterschätzer zeigen, dass die stärkste standardisierte Ladung der Bereichsfaktoren (Faktoren erster Ordnung) diejenige des Bereichs Freunde ist, während die niedrigste diejenige des Bereichs Schule ist. Das Ladungsmuster zeigt sich insgesamt relativ heterogen.
6.3.4.4 Model Fit und Modellvergleiche
CFI = 0.958 und NNFI/TLI = 0.94 sind sehr ähnlich wie beim 4-Faktor-Modell. Der RMSEA = 0.053 ist noch etwas niedriger als bei letzterem und nicht signifikant grösser als 0.05 (90 %-CI = [0.027; 0.077]). Der SRMR = 0.06 fällt dagegen etwas höher als beim 4-Faktor-Modell aus.
AIC = 101.372 und BIC = 186.356 (nach der Eid-Formel mit Chi-Quadrat berechnet) sind beide niedriger als die entsprechenden Werte des 4-Faktor-Modells (AIC = 103.433 und BIC = 195.499). Nach diesen Informationskriterien ist also das Modell mit Faktor zweiter Ordnung gegenüber dem 4-Faktor-Modell zu bevorzugen.
Jetzt vergleichen wir noch alle drei Modelle (in aufsteigender Reihenfolge der Anzahl geschätzter Parameter: 3-Faktor-Modell, 4-Faktor-Modell mit Faktor zweiter Ordnung, 4-Faktor-Modell) über sequentielle Likelihood-Ratio-Tests. Die Voraussetzung für die Gültigkeit dieser Tests ist wie wir wissen die Nestung der eingeschränkten Modelle (mit weniger Parameter) in den Modellen mit weniger Restriktionen (mit mehr Parametern). Für das 3-Faktor- und das 4-Faktor-Modell haben wir die Nestung oben nachgewiesen. Aber auch das 4-Faktor-Modell mit Faktor zweiter Ordnung ist im 4-Faktor-Modell genestet: alle Modelle, die die gleichen vier Faktoren erster Ordnung haben, sind im 4-Faktor-Modell genestet, da es sich bei diesem um ein gesättigtes Modell auf der Ebene der latenten Variablen handelt.
anova(fit_mod3f, fit_mod4f_2order, fit_mod4f)
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_mod4f 29 6907.5 6999.6 51.433
fit_mod4f_2order 31 6905.5 6990.4 53.372 1.9395 0.00000 2 0.3792
fit_mod3f 32 6929.6 7011.1 79.522 26.1494 0.31405 1 3.16e-07
fit_mod4f
fit_mod4f_2order
fit_mod3f ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Modellvergleich zeigt, dass das 4-Faktor-Modell mit Faktor zweiter Ordnung nicht signifikant schlechter auf die Daten passt als das weniger sparsame 4-Faktor-Modell (\(\Delta\chi^2=\) 1.9395, \(p =\) 0.3792). Der zweite Test zeigt dagegen einen signifikanten Modellvergleich des 3-Faktor-Modells mit dem 4-Faktor-Modell mit Faktor zweiter Ordnung an (\(\Delta\chi^2=\) 26.1494, \(p =\) 0). Das 3-Faktor-Modell passt also auch hier signifikant schlechter.
Das beste dieser drei Modelle ist also das 4-Faktor-Modell mit Faktor zweiter Ordnung. Dieses weist auch die jeweils niedrigsten von lavaan ausgegebenen Informationskriterien aller Modelle auf (AIC = 6905.5, BIC = 6990.4).