pacman::p_load(tidyverse, nlme, lme4, lmerTest, ggplot2, ggthemes)3 Modelle mit Messwiederholung
3.1 Lineare Trendmodelle | Psychotherapie und Wohlbefinden
Für die folgenden Modelle benutzen wir das Package nlme und dessen Funktion lme(), das für RM-HLM Modelle besser geeignet ist als lme4 mit der Funktion lmer(). Die Syntax unterscheidet sich kaum, der einzige grössere Unterschied bezieht sich auf die Formulierung des zufälligen Teils des Modells: statt + (woche | id) (für einen random effect des Intercepts und des Level-1-Prädiktors woche, die in id genestet sind) schreibt man , random = ~woche | id
Packages und Daten laden:
Wir laden alle Packages mit pacman.
Das Beispiel ist aus dem Buch von Eid, Gollwitzer, und Schmitt (2017). Die Daten sind in den Online-Materialien verfügbar.
Da wir die Variablen teilweise anders benennen und die Variable bedingung direkt mit den korrekten Faktorstufen-Bezeichnungen einlesen wollen, stellen wir sie unter folgendem Link angepasst zur Verfügung:
therapie <- read_csv("https://raw.githubusercontent.com/methodenlehre/data/master/therapie.csv") |>
mutate(
id = as.factor(id),
bedingung = as.factor(bedingung)
)
glimpse(therapie)Rows: 563
Columns: 4
$ id <fct> 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, …
$ woche <dbl> 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 5, 6, 0, 1, 2, 3, 4, …
$ wohlbefinden <dbl> 2.4, 2.0, 3.2, 1.8, 1.6, 2.0, 1.6, 1.6, 3.6, 4.0, 3.4, 3.…
$ bedingung <fct> Kontrollgruppe, Kontrollgruppe, Kontrollgruppe, Kontrollg…summary(therapie) id woche wohlbefinden bedingung
1 : 8 Min. :0.000 Min. :1.000 Kontrollgruppe:276
4 : 8 1st Qu.:1.000 1st Qu.:2.800 Therapiegruppe:287
6 : 8 Median :3.000 Median :3.800
7 : 8 Mean :3.259 Mean :3.717
14 : 8 3rd Qu.:5.000 3rd Qu.:4.800
16 : 8 Max. :7.000 Max. :6.000
(Other):515 # nur Therapiegruppe
therapie_gr1 <- therapie |>
filter(bedingung == "Therapiegruppe")3.1.1 Level-1-Modelle (nur Therapiegruppe)
Eine Psychotherapeutin erhebt zu acht Messzeitpunkten das Wohlbefinden ihrer \(n = 41\) Klienten mithilfe eines stetigen Merkmals, einmal zu Beginn der Therapie und dann in den folgenden sieben Wochen jeweils einmal im Anschluss an die jeweilige Therapiesitzung. Sie nimmt an, dass das Wohlbefinden mit jeder Woche (Therapiesitzung) konstant steigt, d.h. dass die UV Messzeitpunkt kodiert mit den Werten 0 bis 7 für die Messungen beginnend mit der Baseline vor Beginn der Therapie \((X= 0)\) bis nach der siebten Therapiewoche \((X = 7)\) einen positiven linearen Trend aufweist.
3.1.1.1 Intercept-Only-Modell (Modell 1) und Intraklassenkorrelation
Wir können davon ausgehen, dass sich die Personen in Bezug auf ihr Wohlbefinden insgesamt unterscheiden und es daher substantielle Level-2-Varianz in der AV gibt. Trotzdem wollen wir den Anteil der Level-2-Varianz (Personenvarianz) an der Gesamtvarianz der abhängigen Variablen quantifizieren (Intraklassenkorrelation).
Das Intercept-Only-Modell enthält keine Prädiktorvariable, nur der Intercept wird als Kombination eines festen (durchschnittlichen) Effekts und einer zufälligen Abweichung von diesem (Level-2-Residuum, Abweichung des durchschnittlichen Wohlbefindens einer Person vom Durchschnitt aller Personen) modelliert:
Gesamtmodell: \(\boldsymbol {WB_{mi}=\gamma_{00} + \upsilon_{0i}+\epsilon_{mi}}\)
\(~\)
intercept.only <- lme(wohlbefinden ~ 1,
random = ~ 1 | id,
therapie_gr1, method = "ML"
)
summary(intercept.only)Linear mixed-effects model fit by maximum likelihood
Data: therapie_gr1
AIC BIC logLik
857.5725 868.551 -425.7863
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 1.041132 0.9042715
Fixed effects: wohlbefinden ~ 1
Value Std.Error DF t-value p-value
(Intercept) 3.821784 0.1718299 246 22.24167 0
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.56699824 -0.48832807 0.05519999 0.58938383 3.07033213
Number of Observations: 287
Number of Groups: 41 Da lme() standardmässig nur die Standardabweichungen der random effects ausgibt, benutzt man die Funktion VarCorr(), um zusätzlich auch die Varianzen zu erhalten:
VarCorr(intercept.only)id = pdLogChol(1)
Variance StdDev
(Intercept) 1.0839548 1.0411315
Residual 0.8177069 0.9042715Intraklassenkorrelation: \(\hat\rho = \frac{\hat\sigma^2_{\upsilon_0}}{\hat\sigma^2_{\upsilon_0}+ \hat\sigma^2_\varepsilon} = \frac {1.084}{1.084+0.8177} = 0.57\)
\(\Rightarrow\) 57 % der Gesamtvarianz sind auf Level-2-(Personen-)Unterschiede im Wohlbefinden zurückzuführen.
3.1.1.2 Random-Intercept-Modell (Modell 2)
Gibt es insgesamt (d.h. im Durchschnitt über alle Personen) einen konstanten (= linearen) Anstieg des Wohlbefindens über die Dauer der Therapie?
Berechnen Sie ein Random-Intercept-Modell (Modell 2) mit dem Level-1-Prädiktor woche (Messzeitpunkte mit den Werten 0-7) und und bestimmen Sie den Anteil der durch diesen linearen Trend erklärten Level-1-Varianz der AV wohlbefinden.
Dieses Modell enthält einen Level-1-Prädiktor, der jedoch als fester Effekt konzeptualisiert wird (kein Random Slope, nur Random Intercept).
Gesamtmodell: \(\boldsymbol {WB_{mi}=\gamma_{00} + \gamma_{10} \cdot WOCHE_{mi} + \upsilon_{0i}+\varepsilon_{mi}}\)
\(~\)
random.intercept <- lme(wohlbefinden ~ woche,
random = ~ 1 | id,
therapie_gr1, method = "ML"
)
summary(random.intercept)Linear mixed-effects model fit by maximum likelihood
Data: therapie_gr1
AIC BIC logLik
835.5876 850.2256 -413.7938
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 1.044078 0.8615528
Fixed effects: wohlbefinden ~ woche
Value Std.Error DF t-value p-value
(Intercept) 3.446048 0.18746082 245 18.382766 0
woche 0.114275 0.02285371 245 5.000283 0
Correlation:
(Intr)
woche -0.4
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.8761965 -0.5191788 0.1015888 0.5007727 3.3528652
Number of Observations: 287
Number of Groups: 41 VarCorr(random.intercept)id = pdLogChol(1)
Variance StdDev
(Intercept) 1.0900982 1.0440777
Residual 0.7422733 0.8615528Die Ergebnisse zeigen, dass der fixed effect von woche positiv signifikant ist mit \(\hat\gamma_{10} = 0.114\). Über alle Klienten hinweg steigt das vorhergesagte Wohlbefinden also mit jeder Therapiewoche um 0.114 Einheiten an.
Wieviel Level-1-Varianz wurde durch woche erklärt?
\(R^2_{Level-1} = \frac{\hat\sigma^2_{\varepsilon_1} - \hat\sigma^2_{\varepsilon_2}}{\hat\sigma^2_{\varepsilon_1}} = \frac{{0.8177}-{0.7423}}{0.8177} = {0.0922}\)
\(\Rightarrow\) ca. 9.22 % der Level-1-Varianz von wohlbefinden wurde durch woche (linearer Trend) erklärt.
3.1.1.3 Random-Coefficients-Modell (Modell 3)
Variiert der Effekt von woche (linearer Trend) signifikant zwischen den Personen?
Berechnen Sie ein Random-Coefficients-Modell (Modell 3) und überprüfen Sie mittels LR-Test (Vergleich mit Random-Intercept-Modell), ob sich die zufälligen Regressionsgewichte von woche signifikant zwischen den Personen (= Level-2-Einheiten) unterscheiden (Test von \({\hat\sigma^2_{\upsilon_1}}\) und \({\hat\sigma_{\upsilon_0\upsilon_1}}\) gegen 0).
Gesamtmodell: \(\boldsymbol {WB_{mi}=\gamma_{00} + \gamma_{10} \cdot WOCHE_{mi} + \upsilon_{0i} + \upsilon_{1i} \cdot WOCHE_{mi} + \varepsilon_{mi}}\)
\(~\)
random.coefficients <- lme(wohlbefinden ~ woche,
random = ~ woche | id,
therapie_gr1, method = "ML"
)
summary(random.coefficients)Linear mixed-effects model fit by maximum likelihood
Data: therapie_gr1
AIC BIC logLik
830.5041 852.461 -409.252
Random effects:
Formula: ~woche | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 1.0290556 (Intr)
woche 0.1381025 -0.182
Residual 0.8005709
Fixed effects: wohlbefinden ~ woche
Value Std.Error DF t-value p-value
(Intercept) 3.455749 0.18260414 245 18.924809 0e+00
woche 0.114028 0.03074723 245 3.708548 3e-04
Correlation:
(Intr)
woche -0.384
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.78023820 -0.45874982 0.05703886 0.46723020 3.37849517
Number of Observations: 287
Number of Groups: 41 VarCorr(random.coefficients)id = pdLogChol(woche)
Variance StdDev Corr
(Intercept) 1.05895541 1.0290556 (Intr)
woche 0.01907231 0.1381025 -0.182
Residual 0.64091383 0.8005709 Die Standardabweichung des Effekts von Woche ist \(\sqrt {\hat \sigma^2_{\upsilon_1}} = \hat \sigma_{\upsilon_1} = 0.1381\). Diese kann man sich als eine Art durchschnittliche Abweichung des linearen Trends einer Person vom durchschnittlichen linearen Trend vorstellen.
Schauen wir uns dazu mit ranef() einen Teil der Level-2-Residuen des woche-Effekts an:
ranef(random.coefficients)["woche"] |>
round(2) |>
tail(20) woche
52 0.00
54 0.00
58 0.05
59 -0.03
61 -0.04
64 0.14
66 -0.04
67 0.05
68 -0.15
71 0.00
72 -0.12
74 0.02
75 0.11
80 0.00
81 -0.11
83 0.06
84 -0.05
85 -0.27
88 -0.04
91 0.24Es handelt sich wohlgemerkt um die Residuen des Random Slopes, also um die Abweichungen vom durchschnittlichen woche-Effekt \(\hat\gamma_{10} = 0.114\). Die Standardabweichung dieser Abweichungswerte (und damit auch der individuellen woche-Effekte) ist wie schon gesagt \(\hat \sigma_{\upsilon_1} = 0.1381\).
Wenn wir das Random-Coefficients-Modell mittels LR-Test mit dem Random-Intercept-Modell vergleichen, werden zwei Parameter gleichzeitig getestet: die Level-2-Varianz des Slopes (\(\hat\sigma^2_{\upsilon_1}\)) und die Level-2-Kovarianz/Korrelation zwischen Intercept und Slope (\(\hat\sigma_{\upsilon_0\upsilon_1}\)).
anova(random.coefficients, random.intercept) Model df AIC BIC logLik Test L.Ratio
random.coefficients 1 6 830.5041 852.4610 -409.2520
random.intercept 2 4 835.5876 850.2256 -413.7938 1 vs 2 9.083551
p-value
random.coefficients
random.intercept 0.0107Das Ergebnis zeigt einen signifikanten LR-Test, die Klienten der Therapiegruppe unterscheiden sich also signifikant bezüglich der (linearen) Veränderung des Wohlbefindens über den Therapieverlauf. Die exakte Bestimmung des p-Werts erfolgt durch die Mittelung der p-Werte der beiden Verteilungen (oder durch Vergleich mit dem kritischen Wert von 5.14 für diese Mischverteilung):
0.5 * pchisq(9.083551, 1, lower.tail = FALSE) +
0.5 * pchisq(9.083551, 2, lower.tail = FALSE)[1] 0.00661683\(~\)
Code
therapie_gr1$random.coefficients.preds <- predict(random.coefficients)
ggplot(aes(x = woche, y = random.coefficients.preds, group = id), data = therapie_gr1) +
geom_smooth(aes(color = id), method = "lm", se = FALSE, fullrange = TRUE, linewidth = .2) +
geom_smooth(aes(group = 1), method = "lm", se = FALSE, fullrange = TRUE, color = "black") +
ggtitle("Lineares Random-Coefficients-Modell (nur Therapiegruppe)") +
geom_jitter(aes(y = wohlbefinden, color = id), alpha = .4, width = 0.1, height = 0.1) +
guides(color = "none") + # Legends removed
xlab("Woche") +
ylab("Wohlbefinden") +
theme_tufte()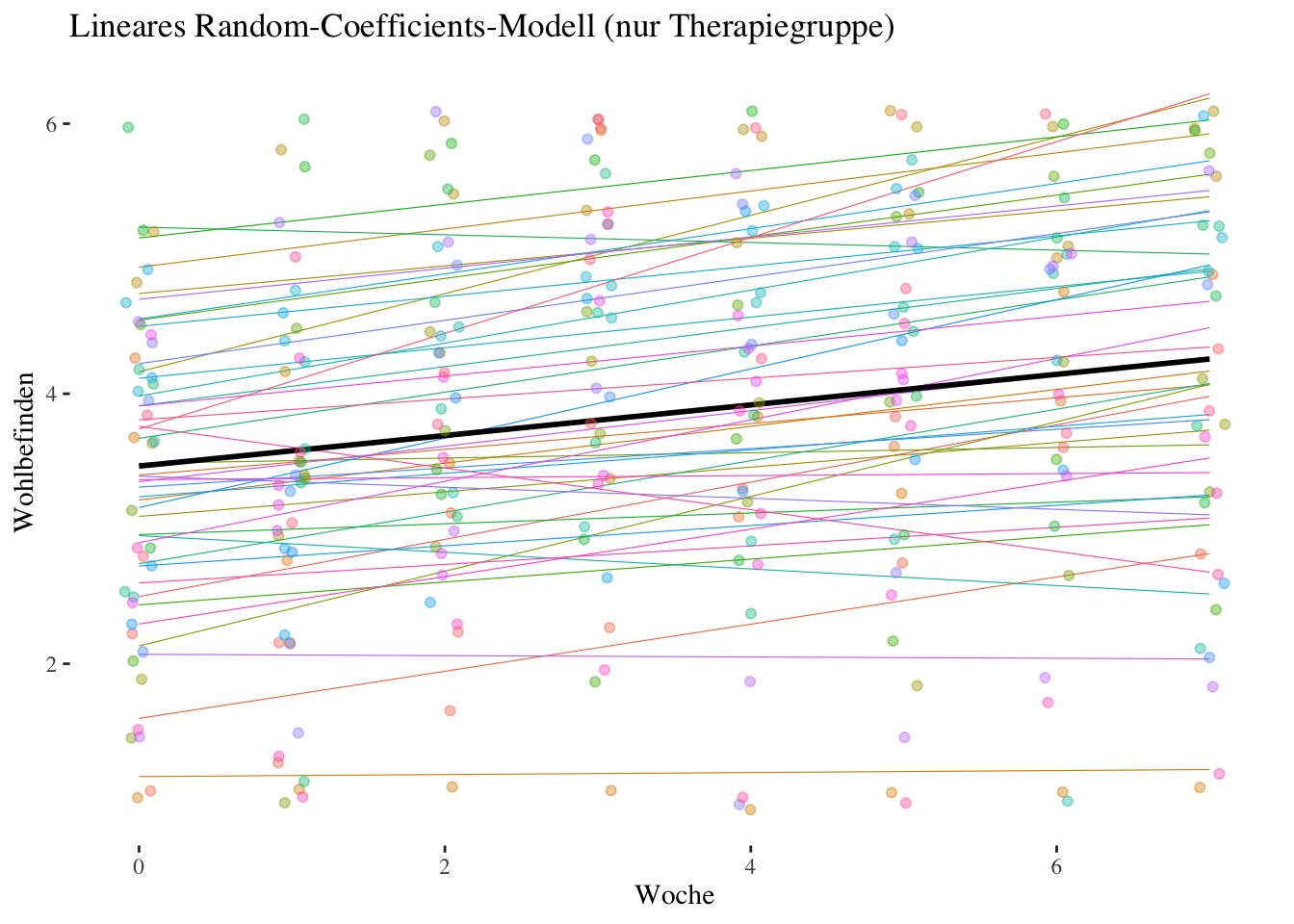
3.1.2 Level-2-Modelle (Therapie- und Kontrollgruppe)
Zusätzlich zu der in den Aufgaben 1-3 betrachteten Therapiegruppe \((n = 41)\) wurde auch eine Kontrollgruppe erhoben \((n = 44)\). Die Dummy-Variable bedingung ist jetzt ein Level-2-(Personen-)Merkmal \(Z\). Wir erwarten, dass der lineare Anstieg des Wohlbefindens in der Therapiegruppe stärker ausfällt als in der Kontrollgruppe (Referenzkategorie von bedingung).
3.1.2.1 Slope-as-Outcome Modell (Modell 5)
Ist die Cross-Level-Interaktion signifikant und geht sie in die erwartete Richtung? Berechnen Sie für die Gesamtstichprobe ein Slope-as-Outcome Modell (Modell mit Cross-Level-Interaktion, Modell 5) mit dem Level-2-Prädiktor bedingung.
Level-1-Modell:
\(\boldsymbol {WB_{mi}=\beta_{0i} + \beta_{1i} \cdot WOCHE_{mi} + \varepsilon_{mi}}\)
Level-2-Modell:
\(\boldsymbol {\beta_{0i}=\gamma_{00} + \gamma_{01} \cdot BEDINGUNG_i + \upsilon_{0i}}\)
\(\boldsymbol {\beta_{1i}=\gamma_{10} + \gamma_{11} \cdot BEDINGUNG_i + \upsilon_{1i}}\)
Gesamtmodell:
\(\boldsymbol {WB_{mi}=\gamma_{00} + \gamma_{10} \cdot WOCHE_{mi} + \gamma_{01} \cdot BEDINGUNG_i + }\) \(\boldsymbol { + \gamma_{11} \cdot WOCHE_{mi} \cdot BEDINGUNG_i + \upsilon_{0i} + \upsilon_{1i} \cdot WOCHE_{mi} + \varepsilon_{mi}}\)
Wichtig
Jetzt muss der vollständige Datensatz therapie verwendet werden!
slope.outcome <- lme(wohlbefinden ~ woche * bedingung,
random = ~ woche | id,
data = therapie, method = "ML"
)
summary(slope.outcome)Linear mixed-effects model fit by maximum likelihood
Data: therapie
AIC BIC logLik
1562.275 1596.941 -773.1373
Random effects:
Formula: ~woche | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 1.0847725 (Intr)
woche 0.1388061 -0.26
Residual 0.7409710
Fixed effects: wohlbefinden ~ woche * bedingung
Value Std.Error DF t-value p-value
(Intercept) 3.591048 0.18137152 476 19.799404 0.0000
woche -0.007404 0.03038093 476 -0.243695 0.8076
bedingungTherapiegruppe -0.133607 0.26096310 83 -0.511975 0.6100
woche:bedingungTherapiegruppe 0.121185 0.04251483 476 2.850423 0.0046
Correlation:
(Intr) woche bdngnT
woche -0.393
bedingungTherapiegruppe -0.695 0.273
woche:bedingungTherapiegruppe 0.281 -0.715 -0.400
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.17091724 -0.47081098 0.03428825 0.49678310 3.62043764
Number of Observations: 563
Number of Groups: 85 VarCorr(slope.outcome)id = pdLogChol(woche)
Variance StdDev Corr
(Intercept) 1.17673129 1.0847725 (Intr)
woche 0.01926715 0.1388061 -0.26
Residual 0.54903808 0.7409710 Die Cross-Level-Interaktion ist signifikant positiv mit \(\hat\gamma_{11} = 0.121\). In der Therapiegruppe ist die Steigung von woche - die lineare Zunahme des Wohlbefindens pro Woche - also um 0.121 höher als in der Kontrollgruppe.
Der Haupteffekt von woche \((\hat\gamma_{10} = -0.007)\) ist jetzt der bedingte Effekt (simple slope) von woche in der Kontrollgruppe. In der Kontrollgruppe gibt es daher keine signifikante Zunahme des Wohlbefindens über den Therapieverlauf. Der Haupteffekt von Bedingung \((\hat\gamma_{01} = -0.134)\) ist jetzt der Unterschied im Wohlbefinden zwischen den beiden Gruppen bei der ersten Messung \((woche= 0)\). Der Unterschied zu Beginn war also nicht signifikant.
Welcher Anteil der Varianz des linearen Trendeffekts von woche wird durch bedingung erklärt? Oder um es anders auszudrücken: Um welchen Anteil reduziert sich \({\hat\sigma^2_{\upsilon_1}}\) im Vergleich zu einem Modell ohne CLI-Effekt? Dazu muss zusätzlich ein Intercept-as-Outcome-Modell (Modell 4) berechnet werden, das sich nur dadurch von Modell 5 unterscheidet, dass es keine CLI enthält.
Intercept-as-Outcome Modell (Modell 4)
intercept.outcome <- lme(wohlbefinden ~ woche + bedingung,
random = ~ woche | id,
data = therapie, method = "ML"
)
summary(intercept.outcome)Linear mixed-effects model fit by maximum likelihood
Data: therapie
AIC BIC logLik
1567.995 1598.328 -776.9973
Random effects:
Formula: ~woche | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 1.0978840 (Intr)
woche 0.1528629 -0.296
Residual 0.7401163
Fixed effects: wohlbefinden ~ woche + bedingung
Value Std.Error DF t-value p-value
(Intercept) 3.445564 0.1749099 477 19.699078 0.0000
woche 0.054394 0.0224303 477 2.425020 0.0157
bedingungTherapiegruppe 0.165298 0.2391333 83 0.691236 0.4913
Correlation:
(Intr) woche
woche -0.302
bedingungTherapiegruppe -0.659 -0.020
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.126104779 -0.466024529 0.007887565 0.492033382 3.585481939
Number of Observations: 563
Number of Groups: 85 VarCorr(intercept.outcome)id = pdLogChol(woche)
Variance StdDev Corr
(Intercept) 1.20534930 1.0978840 (Intr)
woche 0.02336708 0.1528629 -0.296
Residual 0.54777210 0.7401163 Anteil der durch bedingung erklärten Slope-Varianz:
\(R^2_{Cross-level} = \frac{\hat\sigma^2_{\upsilon_14} - \hat\sigma^2_{\upsilon_15}}{\hat\sigma^2_{\upsilon_14}} = \frac{{0.0234}-{0.0193}}{0.0234} = {0.1752}\)
\(\Rightarrow\) 17.52 % der Varianz zwischen den Personen in Bezug auf den linearen Trend (Effekt von woche) können durch die Zugehörigkeit zur Therapie- versus Kontrollgruppe erklärt werden.
Zu guter Letzt können wir noch überprüfen, ob die im Modell 5 verbliebene Slope-Varianz \({\hat\sigma^2_{\upsilon_1}} = 0.0193\) noch signifikant ist. Den entsprechenden Modellvergleich erhält man über ranova(). Diese Funktion ist aber nur für mit lmer() aus lme4 gefittete Modelle verfügbar. Bei den linearen Trendmodellen macht es eigentlich keinen Unterschied, welche der beiden Funktionen/Packages wir verwenden. Daher fitten wir Modell 5 für diesen Zweck einfach nochmals mit lmer() und wenden ranova() dann auf dieses Modell an:
slope.outcome2 <- lmer(wohlbefinden ~ woche * bedingung + (woche | id),
data = therapie, REML = FALSE
)
ranova(slope.outcome2)ANOVA-like table for random-effects: Single term deletions
Model:
wohlbefinden ~ woche + bedingung + (woche | id) + woche:bedingung
npar logLik AIC LRT Df Pr(>Chisq)
<none> 8 -773.14 1562.3
woche in (woche | id) 6 -785.45 1582.9 24.619 2 4.509e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Vergleich zeigt, dass auch nach Berücksichtung der Gruppenzugehörigkeit eine signifikante Zwischen-Personen-Varianz des linearen Trends verbleibt. Auf die Berechnung des exakten p-Werts für diesen Vergleich verzichten wir an dieser Stelle, da der Vergleich auf jeden Fall hochsignifikant ist.
Code
therapie$slope.outcome.preds <- predict(slope.outcome)
ggplot(aes(x = woche, y = slope.outcome.preds, group = id), data = therapie) +
geom_smooth(aes(linetype = bedingung, color = id), method = "lm", se = FALSE, fullrange = TRUE, size = .2) +
geom_smooth(aes(group = bedingung, linetype = bedingung), method = "lm", se = FALSE, fullrange = TRUE, color = "black") +
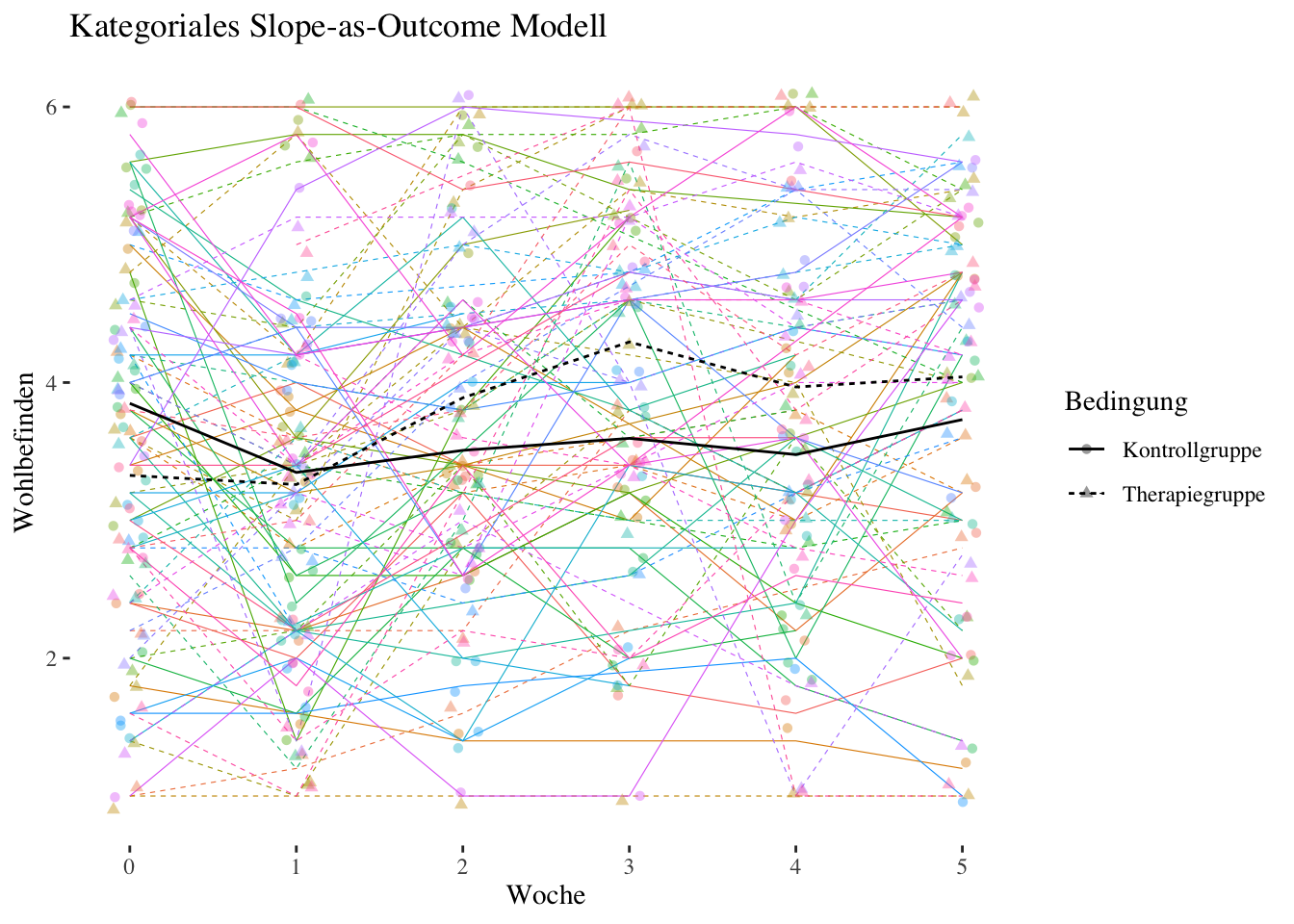
ggtitle("Lineares Slope-as-Outcome Modell") +
guides(color = FALSE) + # Color legend removed
geom_jitter(aes(y = wohlbefinden, shape = bedingung, color = id), alpha = .4, width = 0.1, height = 0.1) +
labs(linetype = "Bedingung", shape = "Bedingung") +
xlab("Woche") +
ylab("Wohlbefinden") +
theme_tufte()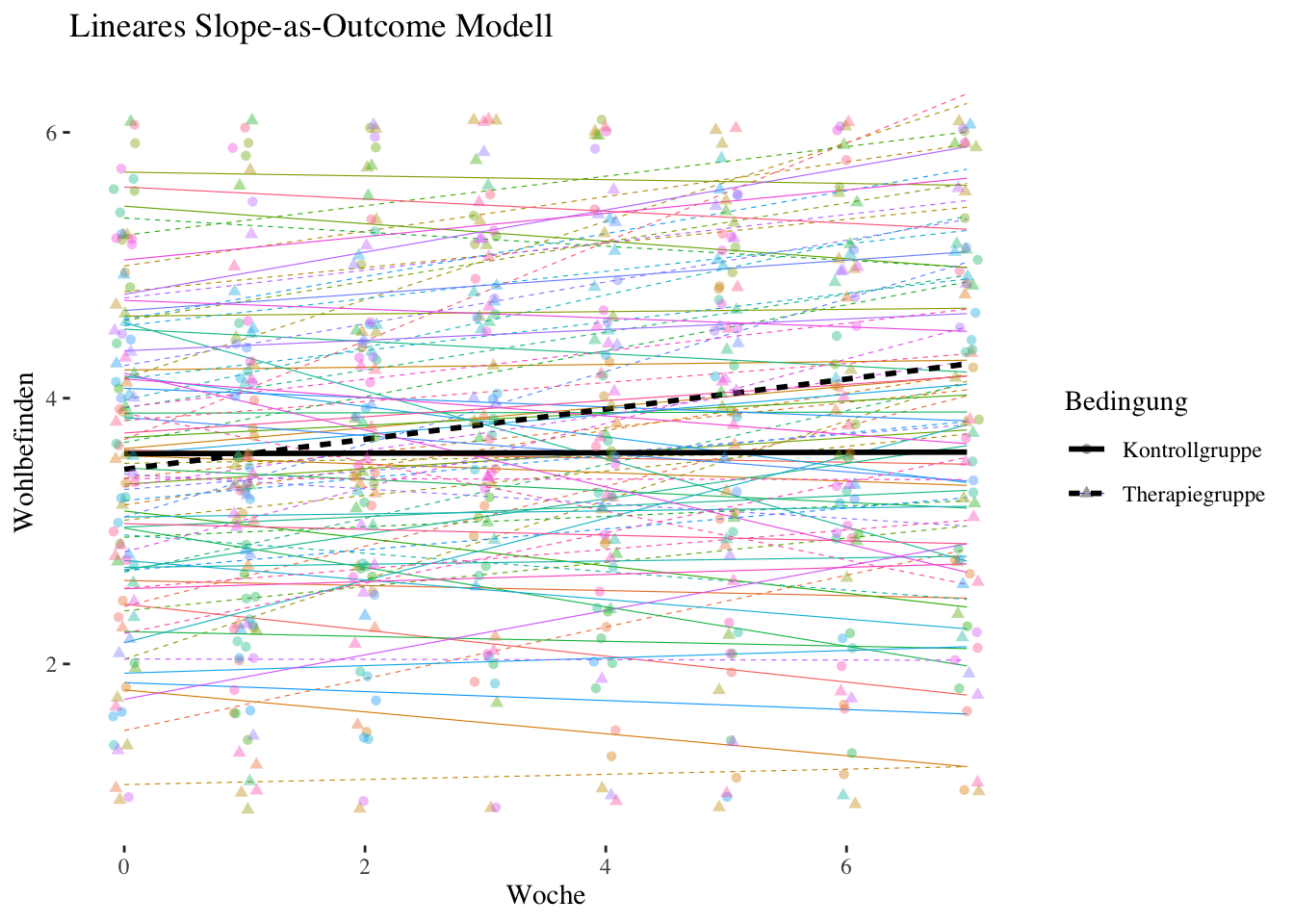
\(~\)
3.1.3 Zusammenfassung
Im Intercept-Only-Modell (Modell 1) der Therapiegruppe waren 57 % der Varianz der abhängigen Variablen wohlbefinden auf Unterschiede zwischen den Personen zurückzuführen. Auch wenn wir die Level-2-Varianz hier nicht auf Signifikanz getestet haben, ist offensichtlich, dass sie substantiell ist und wir daher den Personenfaktor berücksichtigen müssen (etwas anderes wäre auch nicht zu erwarten - Varianz zwischen Personen in Bezug auf ein psychologisches Merkmal gibt es so gut wie immer).
Im Random-Intercept-Modell (Modell 2) der Therapiegruppe sahen wir, dass der Effekt von woche signifikant positiv war, dass es also in dieser Gruppe einen konstanten Anstieg des Wohlbefindens gab. Allerdings konnte dieser lineare Trend nur knapp 10 % der Varianz des Wohlbefindens zwischen den Messzeitpunkten (innerhalb der Personen) erklären. In Folgeanalysen wäre es sinnvoll, die Unterschiede zwischen den Messzeitpunkten mit Hilfe von kontrastkodierten Variablen genauer zu analysieren (s.u.).
Über einen Vergleich von Random-Coefficients-Modell (Modell 3) und Random-Intercept-Modell (Modell 2) konnten wir feststellen, dass sich der lineare Anstieg des Wohlbefindens zwischen den Personen signifikant unterscheidet, dass also manche Personen einen stärkeren, andere einen schwächeren (bzw. manche sogar negativen) linearen Trend des Wohlbefindens aufwiesen.
Im Modell mit Cross-Level-Interaktion (Modell 5) haben wir zuletzt mit allen Daten (inkl. Kontrollgruppe) untersucht, ob sich in der Therapiegruppe ein stärkerer Anstieg des Wohlbefindens ergab. Die signifikante und vom Vorzeichen her positive CLI zeigte uns, dass genau dies der Fall war. Ein substantieller Anteil (17.5 %) der Unterschiedlichkeit der Verläufe zwischen den Personen war auf die Gruppenzugehörigkeit zurückzuführen. Diesen Wert erhielten wir aus dem Vergleich der Slope-Varianzen aus Modell 4 (Intercept-as-Outcome-Modell) und Modell 5.
3.2 Kontrastmodelle | Psychotherapie und Wohlbefinden
In Kontrastmodellen werden die Veränderungen über die Messzeitpunkte statt über einen linearen Trend direkt als (Mittelwerts-)Unterschiede zwischen den Messzeitpunkten mit Hilfe von Codiervariablen (hier: Dummy-Codierung) modelliert. Es handelt sich also um eine Art Varianzanalyse mit Messwiederholung, mit dem HLM-Kontrast-Modell sind aber weniger strenge Annahmen in Bezug auf die Varianz-Kovarianzstruktur verbunden als in der Varianzanalyse mit Messwiederholung (dort: Compound Symmetry bzw. Sphärizität). Für weitere Informationen siehe die Vorlesungsunterlagen.
Wir betrachten ein Kontrastmodell mit 6 Messzeitpunkten (Wochen 0-5). Das Modell mit allen 8 Messzeitpunkten braucht wegen seiner Komplexität sehr viel Rechenzeit und ist daher für diese Übung ungeeignet.
Erstellen des Datensatzes nur für die Therapiegruppe beschränkt auf die Wochen 0-5 mit neuer Faktorvariable woche_f:
therapie05_gr1 <- therapie_gr1 |>
filter(woche <= 5) |>
mutate(woche_f = as.factor(woche))Erstellen des Datensatzes für beide Gruppen beschränkt auf die Wochen 0-5 mit neuer Faktorvariable woche_f:
therapie05 <- therapie |>
filter(woche <= 5) |>
mutate(woche_f = as.factor(woche))3.2.1 Level-1-Modelle (nur Therapiegruppe)
Bevor wir uns dem Random-Coefficients-Modell (Modell 3) als endgültigen Kontrastmodell zuwenden, wie es in Eid, Gollwitzer, und Schmitt (2017) als saturiertes Modell ohne Level-1-Residuum beschrieben ist, wollen wir zunächst ein Random-Intercept-Modell betrachten (inkl. Level-1-Residuum).
Dieses Modell dient einerseits der Testung des Gesamteffekts von woche_f (über einen Modellvergleich mit dem Intercept-Only-Modell) sowie der Überprüfung der Frage, ob überhaupt ein Kontrastmodell notwendig ist oder ob ggf. das oben besprochene lineare Trendmodell bzw. ein Modell mit polynomialen Trends, das weniger Parameter schätzt als das Kontrastmodell, ausreicht.
3.2.1.1 Random-Intercept-Modell (Modell 2)
random.intercept.05.c <- lme(wohlbefinden ~ woche_f,
random = ~ 1 | id,
data = therapie05_gr1,
method = "ML"
)
summary(random.intercept.05.c)Linear mixed-effects model fit by maximum likelihood
Data: therapie05_gr1
AIC BIC logLik
667.7816 695.1459 -325.8908
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 1.019026 0.8380026
Fixed effects: wohlbefinden ~ woche_f
Value Std.Error DF t-value p-value
(Intercept) 3.298903 0.2127571 180 15.505486 0.0000
woche_f1 -0.029438 0.1933249 180 -0.152271 0.8791
woche_f2 0.593702 0.1975901 180 3.004716 0.0030
woche_f3 0.987673 0.1998182 180 4.942858 0.0000
woche_f4 0.661877 0.1981677 180 3.339985 0.0010
woche_f5 0.713265 0.1965381 180 3.629141 0.0004
Correlation:
(Intr) wch_f1 wch_f2 wch_f3 wch_f4
woche_f1 -0.468
woche_f2 -0.456 0.502
woche_f3 -0.454 0.499 0.490
woche_f4 -0.458 0.503 0.494 0.495
woche_f5 -0.461 0.507 0.498 0.496 0.500
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.96644596 -0.54297993 0.04957161 0.53007502 3.08147650
Number of Observations: 226
Number of Groups: 41 VarCorr(random.intercept.05.c)id = pdLogChol(1)
Variance StdDev
(Intercept) 1.0384137 1.0190259
Residual 0.7022484 0.8380026Die Ergebnisse zeigen einen nicht signifikanten Effekt der ersten Dummy-Variable \((D_1)\) von \(\hat\gamma_{10}= -0.029\). Zwischen der Baseline und Woche 1 zeigt sich in der Therapiegruppe also keine statistisch bedeutsame Veränderung des Wohlbefindens. Die Effekte der zweiten bis fünften Dummy-Variablen \((D_2 - D_5)\) sind dagegen signifikant mit \(\hat\gamma_{20}= 0.594, \hat\gamma_{30}= 0.988, \hat\gamma_{40}= 0.662, \hat\gamma_{50}= 0.713\). Von Woche 0 zu den Wochen 2, 3, 4 und 5 zeigt sich also jeweils eine statistisch bedeutsame Zunahme des Wohlbefindens.
Gibt es auch einen signifikanten Gesamteffekt? Dazu müssen wir das Random-Intercept-Modell mit einem Modell ohne Prädiktoren vergleichen, also einem Intercept-Only-Modell:
intercept.only.05 <- lme(wohlbefinden ~ 1,
random = ~ 1 | id,
data = therapie05_gr1,
method = "ML"
)
anova(random.intercept.05.c, intercept.only.05) Model df AIC BIC logLik Test L.Ratio
random.intercept.05.c 1 8 667.7816 695.1459 -325.8908
intercept.only.05 2 3 697.8729 708.1345 -345.9365 1 vs 2 40.09131
p-value
random.intercept.05.c
intercept.only.05 <.0001Ja, auch insgesamt zeigen sich Unterschiede zwischen den verschiedenen Messzeitpunkten in der Variable wohlbefinden.
Vergleich mit dem linearen Modell
Es könnte ja sein, dass die oben berechneten linearen Modelle ausreichen, um die Veränderung des Wohlbefindens über die Zeit zu modellieren. Das können wir über einen Modellvergleich des RI-Kontrast-Modells mit dem RI-linearen Modell herausfinden. Das lineare Modell haben wir oben für alle 8 Messzeitpunkte (0-7) berechnet. Wir müssen es daher nochmal beschränkt auf die ersten sechs Messzeitpunkte berechnen, um den Vergleich durchführen zu können.
random.intercept.05.l <- lme(wohlbefinden ~ woche,
random = ~ 1 | id,
data = therapie05_gr1,
method = "ML"
)
anova(random.intercept.05.c, random.intercept.05.l) Model df AIC BIC logLik Test L.Ratio
random.intercept.05.c 1 8 667.7816 695.1459 -325.8908
random.intercept.05.l 2 4 676.1171 689.7992 -334.0586 1 vs 2 16.33551
p-value
random.intercept.05.c
random.intercept.05.l 0.0026Das lineare Modell passt signifikant schlechter auf die Daten als das Kontrast-Modell. Somit ist es notwendig, die nicht-linearen Anteile des Verlaufs zu berücksichtigen.
Vertiefung: Vergleich mit polynomialen Trendmodellen
Man kann jetzt noch überprüfen, ob ggf. ein polynomiales Trendmodell (mit quadratischem, kubischem oder quartischem) Effekt ausreicht, man also die Nicht-Linearität des Verlaufs nicht unbedingt mit dem Kontrastmodell beschreiben muss, sondern auf ein (etwas) sparsameres Modell ausweichen kann.
Um das Kontrastmodell mit den verschiedenen polynomialen Trendmodellen vergleichen zu können, müssen diese zunächst geschätzt werden. Da wir uns hier nicht für die einzelnen Trendeffekte im Detail interessieren, verzichten wir auf die Ausgabe der geschätzten Parameter dieser Modelle mit summary(). Stattdessen führen wir gleich die Modellvergleiche mit dem Kontrastmodell durch:
random.intercept.05.quad <- lme(wohlbefinden ~ woche + I(woche^2),
random = ~ 1 | id,
data = therapie05_gr1,
method = "ML"
)
random.intercept.05.cub <- lme(wohlbefinden ~ woche + I(woche^2) + I(woche^3),
random = ~ 1 | id,
data = therapie05_gr1,
method = "ML"
)
random.intercept.05.quart <- lme(wohlbefinden ~ woche + I(woche^2) + I(woche^3) + I(woche^4),
random = ~ 1 | id,
data = therapie05_gr1,
method = "ML"
)
anova(random.intercept.05.c, random.intercept.05.quart, random.intercept.05.cub, random.intercept.05.quad, random.intercept.05.l) Model df AIC BIC logLik Test L.Ratio
random.intercept.05.c 1 8 667.7816 695.1459 -325.8908
random.intercept.05.quart 2 7 666.0751 690.0189 -326.0376 1 vs 2 0.293525
random.intercept.05.cub 3 6 671.3163 691.8395 -329.6582 2 vs 3 7.241181
random.intercept.05.quad 4 5 671.7553 688.8580 -330.8777 3 vs 4 2.439023
random.intercept.05.l 5 4 676.1171 689.7992 -334.0586 4 vs 5 6.361775
p-value
random.intercept.05.c
random.intercept.05.quart 0.5880
random.intercept.05.cub 0.0071
random.intercept.05.quad 0.1183
random.intercept.05.l 0.0117Der hierarchische Modellvergleich der fünf Modelle (Kontrastmodell, Modell mit quartischem Trend I(woche^4), Modell mit kubischem Trend I(woche^3), Modell mit quadratischem Trend I(woche^2), Modell mit linearem Trend woche) zeigt, dass sich der Model-Fit (Devianz) des Kontrastmodells nicht signifikant von dem des quartischen Trendmodells unterscheidet (\(p = 0.5880\)), sich aber das letztere signifikant vom kubischen Trendmodell unterscheidet (\(p = 0.0071\)). Das bedeutet, dass für eine angemessene Beschreibung des Verlaufs des Wohlbefindens (mindestens) ein quartisches Trendmodell (d.h. ein Modell mit mindestens drei Richtungsänderungen) benötigt wird. Dass der folgende Modellvergleich zwischen dem kubischen Trendmodell und dem quadratischen Trendmodell dann wieder nicht signifikant ist (\(p = 0.1183\)), spielt keine Rolle mehr, da wir beim ersten signifikanten Modellvergleich (quartisch vs. kubisch) stoppen müssen, da das kubische Trendmodell schon keine ausreichende Passung mehr aufweist.
Für unsere Zwecke ist es nicht sonderlich relevant, dass wir streng genommen kein Kontrastmodell benötigen, sondern ein quartisches polynomiales Trendmodell (mit einem Parameter weniger) ausreicht, da dieses nur geringfügig weniger komplex und zudem schwieriger zu interpretieren ist als das Kontrastmodell.
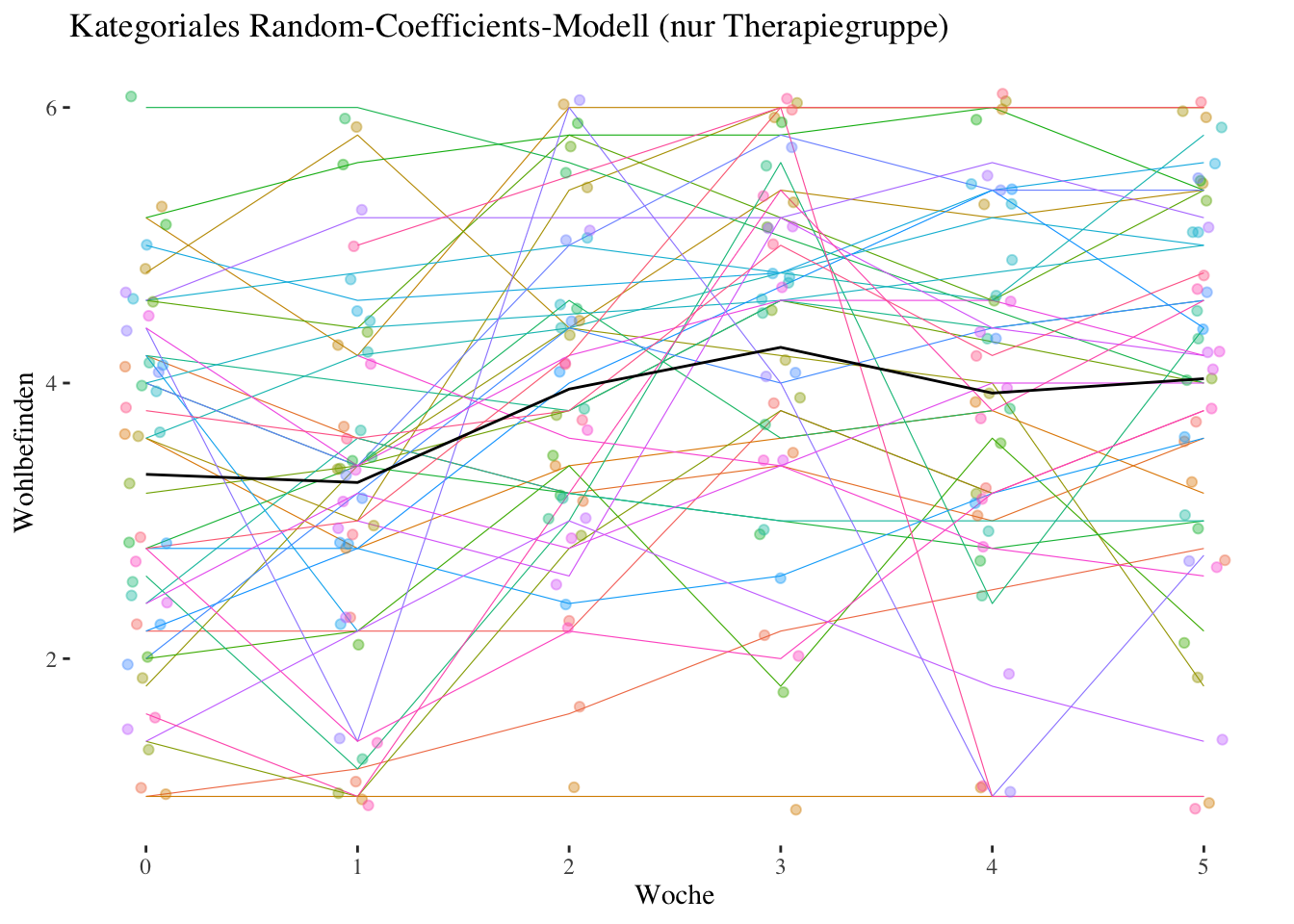
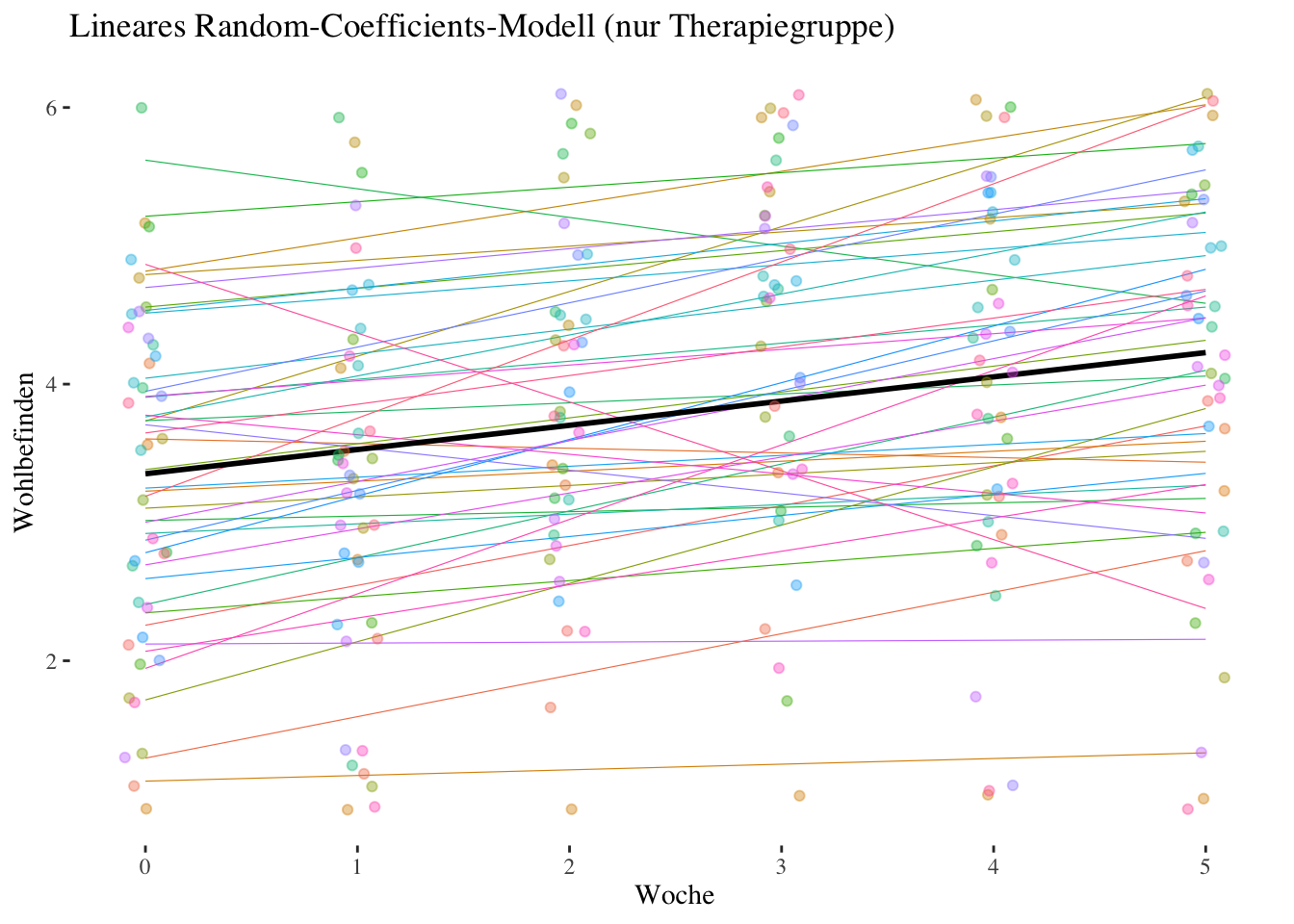
3.2.1.2 Random-Coefficients-Modell (Modell 3)
Bei den Kontrastmodellen spielt das Random-Coefficients-Modell eine besondere Rolle, da es sich bei diesem Modell um ein saturiertes Modell handelt, d.h. um ein Modell ohne Level-1-Residuum, da auf Ebene 1 alle Variation der Beobachtungen durch die Modellparameter (fixed und random effects) repräsentiert ist. Im Lehrbuch von Eid, Gollwitzer, und Schmitt (2017) wird im Abschnitt zu den Kontrastmodellen nur dieses Random-Coefficients-Modell beschrieben, ein Random-Intercept-Modell wie wir es oben beschrieben haben, wird dort gar nicht erwähnt.
Da die lme()-Funktion - wenn wir sie nicht daran hindern - auch in diesem Modell versucht, eine Level-1-Residualvarianz zu schätzen, müssen wir die lme()-Modellsyntax folgendermassen mit einem control-Argument ergänzen:
control = list(opt = "optim", sigma = 1e-7)
Hier wird zum einen ein Optimizer für den Schätzalgorithmus namens optim festgelegt, und zum anderen sigma, d.h. die Level-1-Residual-Standardabweichung (Quadratwurzel aus der Level-1-Residualvarianz) auf einen sehr kleinen, d.h. sehr nahe bei 0 liegenden Wert festgesetzt (eine Festsetzung auf exakt 0 ist nicht möglich).
random.coefficients.05.c <- lme(wohlbefinden ~ woche_f,
random = ~ woche_f | id,
data = therapie05_gr1,
method = "ML",
control = list(opt = "optim", sigma = 1e-7)
)
summary(random.coefficients.05.c)Linear mixed-effects model fit by maximum likelihood
Data: therapie05_gr1
AIC BIC logLik
-6442.107 -6349.752 3248.053
Random effects:
Formula: ~woche_f | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 1.2845973 (Intr) wch_f1 wch_f2 wch_f3 wch_f4
woche_f1 0.9129692 -0.297
woche_f2 0.8557933 -0.379 0.223
woche_f3 1.2249201 -0.474 0.244 0.592
woche_f4 1.4606758 -0.515 0.432 0.416 0.595
woche_f5 1.3621709 -0.483 0.165 0.314 0.643 0.859
Residual 0.0000001
Fixed effects: wohlbefinden ~ woche_f
Value Std.Error DF t-value p-value
(Intercept) 3.337688 0.2052587 180 16.260884 0.0000
woche_f1 -0.059310 0.1484144 180 -0.399627 0.6899
woche_f2 0.618576 0.1420488 180 4.354675 0.0000
woche_f3 0.921607 0.2020530 180 4.561216 0.0000
woche_f4 0.589726 0.2361702 180 2.497038 0.0134
woche_f5 0.694147 0.2205539 180 3.147289 0.0019
Correlation:
(Intr) wch_f1 wch_f2 wch_f3 wch_f4
woche_f1 -0.313
woche_f2 -0.379 0.236
woche_f3 -0.469 0.255 0.570
woche_f4 -0.515 0.434 0.410 0.582
woche_f5 -0.486 0.183 0.316 0.630 0.851
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-4.884981e-07 -9.381385e-08 6.661338e-09 9.769963e-08 4.529710e-07
Number of Observations: 226
Number of Groups: 41 VarCorr(random.coefficients.05.c)id = pdLogChol(woche_f)
Variance StdDev Corr
(Intercept) 1.650190e+00 1.2845973 (Intr) wch_f1 wch_f2 wch_f3 wch_f4
woche_f1 8.335127e-01 0.9129692 -0.297
woche_f2 7.323822e-01 0.8557933 -0.379 0.223
woche_f3 1.500429e+00 1.2249201 -0.474 0.244 0.592
woche_f4 2.133574e+00 1.4606758 -0.515 0.432 0.416 0.595
woche_f5 1.855509e+00 1.3621709 -0.483 0.165 0.314 0.643 0.859
Residual 1.000000e-14 0.0000001 Die fixed effects Parameter (Effekte der Dummy-Variablen woche_f1 bis woche_f5) des Random-Coefficents-Modells unterscheiden sich nur geringfügig von denen des Random-Intercept-Modells weiter oben, auch hier gibt es signifikante Effekte der Dummy-Variablen woche_f2 bis woche_f5, während der Wohlbefindensunterschied zwischen Woche 0 und Woche 1 (Effekt von woche_f1) nicht signifikant ist.
Zusätzlich bekommen wir die Random-Effects-Varianzen und Korrelationen der Random Intercept/Slopes der Dummy-Variablen ausgegeben. Es zeigt sich, dass die Varianzen der Woche-Effekte mit Zunahme des Abstandes von der Baseline tendenziell grösser werden, also dass die interindividuellen Unterschiede in der Veränderung des Wohlbefindens (d.h. im Vergleich zum Wohlbefinden zu Beginn) im Verlauf der Therapie grösser wurden. Von Interesse sind insbesondere die Korrelationen: In der ersten Spalte von Corr erhalten wir die Korrelationen zwischen Intercept und den Dummy-Effekten, und diese sind alle negativ und werden mit weiter entfernten woche_f Effekten tendenziell grösser. Das bedeutet, dass Personen, die in Woche 0 mit einem relativ hohen Wohlbefinden in die Therapie starten, tendenziell kleinere Wohlbefindenszunahmen aufweisen als Personen, die mit relativ niedrigerem Wohlbefinden starten. Die Korrelationen der Woche-Effekte untereinander sind dagegen alle positiv und näher zusammen liegende Wochen-Effekte sind tendenziell stärker miteinander korreliert. Das spiegelt die Tatsache wider, das Personen, die eine z.B. starke Zunahme des Wohlbefindens von Woche 0 (Baseline) nach Woche 2 (Effekt von woche_f2) erleben, auch eine (relativ zu anderen) starke Zunahme von Woche 0 nach Woche 3 (Effekt von woche_f3) erleben (\(r_{\upsilon_2 \upsilon_3}=0.592\)).
\(~\)
3.2.2 Level-2-Modelle (Therapie- und Kontrollgruppe)
3.2.2.1 Slope-as-Outcome-Modell (Modell 5)
Wir starten gleich mit dem Slope-as-Outcome-Modell, da dieses Modell alles enthält, wofür wir uns interessieren, wenn wir beide Gruppen (Therapie- und Kontrollgruppe) analysieren.
Es handelt sich hier auch wieder um ein Modell mit allen Random Effects, d.h. wie oben um ein saturiertes Modell ohne Level-1-Residuum. Die in diesem Modell enthaltene Cross-Level-Interaktion testet die Unterschiedlichkeit der Dummy-Variablen-Effekte zwischen Therapie- und Kontrollgruppe. Ein positiver CLI-Term bedeutet jeweils, dass der entsprechende Effekt in der Therapiegruppe stärker (positiv) ist als in der Kontrollgruppe.
Dieses Modell muss jetzt mit dem vollständigen Datensatz (alle Gruppen) der Wochen 0-5 geschätzt werden:
slope.outcome.05.c <- lme(wohlbefinden ~ woche_f * bedingung,
random = ~ woche_f | id,
data = therapie05,
method = "ML",
control = list(opt = "optim", sigma = 1e-7)
)
summary(slope.outcome.05.c)Linear mixed-effects model fit by maximum likelihood
Data: therapie05
AIC BIC logLik
-12590.83 -12455.89 6328.416
Random effects:
Formula: ~woche_f | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 1.3504715 (Intr) wch_f1 wch_f2 wch_f3 wch_f4
woche_f1 0.9804844 -0.410
woche_f2 0.8960760 -0.440 0.412
woche_f3 1.0762710 -0.453 0.341 0.546
woche_f4 1.4344052 -0.554 0.672 0.556 0.626
woche_f5 1.4885280 -0.555 0.439 0.422 0.672 0.820
Residual 0.0000001
Fixed effects: wohlbefinden ~ woche_f * bedingung
Value Std.Error DF t-value p-value
(Intercept) 3.829845 0.2071566 346 18.487686 0.0000
woche_f1 -0.479391 0.1523474 346 -3.146697 0.0018
woche_f2 -0.334966 0.1450745 346 -2.308926 0.0215
woche_f3 -0.204510 0.1823108 346 -1.121768 0.2627
woche_f4 -0.290397 0.2344359 346 -1.238704 0.2163
woche_f5 -0.114591 0.2505564 346 -0.457346 0.6477
bedingungTherapiegruppe -0.433488 0.2994563 83 -1.447584 0.1515
woche_f1:bedingungTherapiegruppe 0.357382 0.2206311 346 1.619815 0.1062
woche_f2:bedingungTherapiegruppe 0.886971 0.2082029 346 4.260128 0.0000
woche_f3:bedingungTherapiegruppe 1.075709 0.2559368 346 4.203025 0.0000
woche_f4:bedingungTherapiegruppe 0.821419 0.3300129 346 2.489051 0.0133
woche_f5:bedingungTherapiegruppe 0.732874 0.3478821 346 2.106674 0.0359
Correlation:
(Intr) wch_f1 wch_f2 wch_f3 wch_f4 wch_f5
woche_f1 -0.411
woche_f2 -0.425 0.403
woche_f3 -0.412 0.313 0.480
woche_f4 -0.522 0.636 0.510 0.547
woche_f5 -0.506 0.401 0.371 0.571 0.775
bedingungTherapiegruppe -0.692 0.285 0.294 0.285 0.361 0.350
woche_f1:bedingungTherapiegruppe 0.284 -0.691 -0.278 -0.216 -0.439 -0.277
woche_f2:bedingungTherapiegruppe 0.296 -0.281 -0.697 -0.334 -0.356 -0.259
woche_f3:bedingungTherapiegruppe 0.294 -0.223 -0.342 -0.712 -0.389 -0.406
woche_f4:bedingungTherapiegruppe 0.371 -0.451 -0.363 -0.388 -0.710 -0.550
woche_f5:bedingungTherapiegruppe 0.364 -0.289 -0.267 -0.411 -0.558 -0.720
bdngnT wc_1:T wc_2:T wc_3:T wc_4:T
woche_f1
woche_f2
woche_f3
woche_f4
woche_f5
bedingungTherapiegruppe
woche_f1:bedingungTherapiegruppe -0.418
woche_f2:bedingungTherapiegruppe -0.433 0.411
woche_f3:bedingungTherapiegruppe -0.432 0.333 0.506
woche_f4:bedingungTherapiegruppe -0.539 0.651 0.528 0.579
woche_f5:bedingungTherapiegruppe -0.530 0.423 0.395 0.612 0.792
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-4.973799e-07 -9.325873e-08 8.881784e-09 8.881784e-08 5.151435e-07
Number of Observations: 441
Number of Groups: 85 VarCorr(slope.outcome.05.c)id = pdLogChol(woche_f)
Variance StdDev Corr
(Intercept) 1.823773e+00 1.3504715 (Intr) wch_f1 wch_f2 wch_f3 wch_f4
woche_f1 9.613497e-01 0.9804844 -0.410
woche_f2 8.029522e-01 0.8960760 -0.440 0.412
woche_f3 1.158359e+00 1.0762710 -0.453 0.341 0.546
woche_f4 2.057518e+00 1.4344052 -0.554 0.672 0.556 0.626
woche_f5 2.215716e+00 1.4885280 -0.555 0.439 0.422 0.672 0.820
Residual 1.000000e-14 0.0000001 Die Ergebnisse zeigen, dass alle bis auf den ersten Interaktionsterm signifikant sind. Nur von Woche 0 zu Woche 1 (Interaktionsterm \(D_1 \times Z: \hat\gamma_{11}= 0.357\)) ist der Unterschied zwischen Therapie- und Kontrollgruppe nicht signifikant. Bei allen anderen Kontrasten mit der Baseline gibt es einen signifikanten Unterschied in der Veränderung von Wohlbefinden: Woche 2 (Interaktionsterm \(D_2 \times Z: \hat\gamma_{21}= 0.887\)), Woche 3 (Interaktionsterm \(D_3 \times Z: \hat\gamma_{31}= 1.076\)), Woche 4 (Interaktionsterm \(D_4 \times Z: \hat\gamma_{41}= 0.821\)), Woche 5 (Interaktionsterm \(D_5 \times Z: \hat\gamma_{51}= 0.733\)).
Interessant sind auch die simple slopes von woche_f (Effekte der Dummyvariablen \(D_1 - D_5\)): Diese testen die Veränderungen in der Kontrollgruppe (Referenzkategorie von bedingung). Man sieht, dass es in dieser Gruppe in den ersten beiden Wochen signifikant bergab mit dem Wohlbefinden geht, ehe es sich stabilisiert und ab Woche 3 keine signifikanten Kontraste mit der Baseline mehr zu beobachten sind.
Auch hier brauchen wir streng genommen noch einen Test für den Gesamteffekt der Interaktion (also aller fünf Interaktionsterme zusammen). Diesen bekommen wir über einen Vergleich mit einem Intercept-as-Outcome-Modell, das keine CLI enthält (aber sich darüber hinaus nicht von Modell 5 unterscheidet) :
intercept.outcome.05.c <- lme(wohlbefinden ~ woche_f + bedingung,
random = ~ woche_f | id,
data = therapie05,
method = "ML",
control = list(opt = "optim", sigma = 1e-7)
)
anova(slope.outcome.05.c, intercept.outcome.05.c) Model df AIC BIC logLik Test L.Ratio
slope.outcome.05.c 1 33 -12590.83 -12455.89 6328.416
intercept.outcome.05.c 2 28 -12740.81 -12626.31 6398.404 1 vs 2 139.9745
p-value
slope.outcome.05.c
intercept.outcome.05.c <.0001Wie zu erwarten war, ist die Cross-level-Interaktion auch insgesamt signifikant (\(p < 0.0001\)).
\(~\)
3.2.3 Zusammenfassung
Das RI-Kontrast-Modell (Modell 2) nur für die Therapiegruppe ergab signifikante Zunahmen des Wohlbefindens über die fünf Therapiewochen. Nur das nach der ersten Woche gemessene Wohlbefinden war nicht signifikant höher als das Baseline-Wohlbefinden, alle anderen Kontraste zur Baseline waren signifikant. Wegen der Dummy-Codierung können wir nur Aussagen zu den Baseline-Kontrasten machen, ob sich das Wohlbefinden auch zwischen den einzelnen Wochen (also z.B. von Woche 2 zu Woche 3) signifikant verbessert (bzw. ggf. wieder verschlechtert) hat, können wir mit dieser Codierung nicht feststellen. Um das zu testen, bräuchten wir eine Codierung im Sinne wiederholter Kontraste, die wir uns aber hier nicht näher anschauen. Ausserdem überprüften wir über einen Vergleich mit einem linearen RI-Modell, ob die Linearitätsannahme, die wir im ersten Teil dieser Übung getroffen hatten, angemessen war. Da das lineare Modell signifikant schlechter auf die Daten passte als das Kontrast-Modell, ist letzteres zu bevorzugen. Die Veränderungen über den Therapieverlauf sind also nicht linear, sondern es gibt “Sprünge”. Insbesondere scheint die Verbesserung des Wohlbefindens zwischen den Wochen 1 und 3 am stärksten zu sein (vgl. Plot). In einer Vertiefung betrachteten wir zudem noch polynomiale Trendmodelle: um den Verlauf des Wohlbefindens angemessen zu beschreiben, wird nach den Ergebnissen der Modellvergleiche mindestens ein Modell mit quartischem Trend benötigt, das im Sinne der Anzahl zu schätzender Parameter aber nur wenig “sparsamer” als das Kontrastmodell ist.
Das saturierte RC-Kontrast-Modell (Modell 3) hat uns zusätzlich zu den durchschnittlichen (=festen) Effekten des Woche-Faktors die Varianzen und Kovarianzen dieser Effekte geschätzt. Dort zeigten sich insbesondere negative Korrelationen des personenspezifischen Intercepts mit den Effekten der Wochen 1-5: Personen, die bereits mit einem höheren Wohlbefinden gestartet sind, zeigten tendenziell eine niedrigere Wohlbefindensverbesserung als Personen, die zu Beginn ein niedrigeres Wohlbefinden aufwiesen. Die Effekte der Wochen 1-5 waren dagegen allesamt positiv korreliert.
Der Hauptfokus dieser Analysen lag aber auf dem Slope-as-Outcome-Kontrast-Modell (Modell 5)), das mit dem vollständigen Datensatz (Therapie- und Kontrollgruppe) gerechnet wurde. Hier zeigten sich wie auch schon beim linearen Slope-as-Outcome-Modell bedeutsame Unterschiede zwischen Therapie- und Kontrollgruppe bzgl. der Veränderung des Wohlbefindens über den Therapieverlauf: Mit Ausnahme der Veränderung von der Baseline zur ersten Woche, zeigte sich bezüglich aller anderen Vergleiche mit der Baseline, dass die Veränderung (Verbesserung) des Wohlbefindens in der Therapiegruppe signifikant stärker war als in der Kontrollgruppe.
3.3 Übung
Wir verwenden (echte) Daten aus einem psychologischen Experiment mit Messwiederholung (Beispiel angepasst aus Bates 2010). Die Studie untersuchte den Effekt von Schlafentzug/Schlafmangel auf die Reaktionszeit von Lastwagenfahrerinnen und Lastwagenfahrern (Belenky u. a. 2003). Die Reaktionszeit wurde jeden Tag (über 10 Tage hinweg) getestet. Die Daten, die wir haben, sind ausschliesslich von der Gruppe, die pro Tag nur 3 Stunden schlafen durften. Tatsächlich sind die Daten im Package lme4 gespeichert. Das bedeutet, wir können das Datenfile sleepstudy direkt verwenden, sobald das Package lme4 geladen ist.
Wir können uns zuerst mal die Daten anschauen.
pacman::p_load(lme4, tidyverse, nlme, viridis)
str(sleepstudy)'data.frame': 180 obs. of 3 variables:
$ Reaction: num 250 259 251 321 357 ...
$ Days : num 0 1 2 3 4 5 6 7 8 9 ...
$ Subject : Factor w/ 18 levels "308","309","310",..: 1 1 1 1 1 1 1 1 1 1 ...Wir haben insgesamt 18 Lastwagenfahrerinnen und Lastwagenfahrer (Subject), jeweils den Tag der Testung (Days, 1-10) und die Reaktionszeit (Reaction) für jede Lastwagenfahrerin bzw. Lastwagenfahrer an jedem Tag (insgesamt 180 Beobachtungen). In diesem Beispiel gibt es keine Level-2-Prädiktoren.
plot(sleepstudy)
Dieser sehr basale Plot gibt eine Streudiagramm-Matrix aller Variablen aus. Der Streudiagramm zum Zusammenhang zwischen Days und Reaction berücksichtigt die Gruppierung der Werte innerhalb der einzelnen Lastwagenfahrer nicht. Und das Streudiagramm für Days und Subject ist natürlich komplett sinnfrei…
Wir versuchen daher mal etwas anderes: Jede(r) Lastwagenfahrer(in) bekommt ihren/seinen eigenen Plot für den Zusammenhang von Days und Reaction.
Die Plots sind nach Intercept und Slope geordnet geordnet. Die Farben visualisieren die Höhe der Intercepts.
1. Intraklassenkorrelation
Berechnen Sie die Intraklassenkorrelation. Tipp: Berechnen Sie ein Intercept-Only-Modell.
Lösung
sleep.intercept.only <- lme(Reaction ~ 1,
random = ~ 1 | Subject,
data = sleepstudy, method = "ML"
)
VarCorr(sleep.intercept.only)Subject = pdLogChol(1)
Variance StdDev
(Intercept) 1196.436 34.58954
Residual 1958.865 44.25907Die Berechnung erfolgt analog der der Intraklassenkorrelation im Therapie-Beispiel auf Basis des Intercept-Only-Modells.
Also:
\(\frac{1196.436 }{(1196.436 + 1958.865)} = 0.3792\)
Das bedeutet, dass 38 % der gesamten Varianz der Reaktionszeiten auf (durchschnittliche) Unterschiede zwischen den Personen zurückzuführen sind und im Gegenzug 62 % der Gesamtvarianz innerhalb der Personen zu verorten sind.
2. Lineare Trendmodelle
Schätzen Sie den linearen Trend für die Population der Lastwagenfahrer und begründen Sie, weshalb Sie sich für das Random-Intercept oder für das Random-Coefficients Modell entschieden haben.
Lösung
sleep.random.intercept <- lme(Reaction ~ Days,
random = ~ 1 | Subject,
data = sleepstudy, method = "ML"
)
sleep.random.coefficients <- lme(Reaction ~ Days,
random = ~ Days | Subject,
data = sleepstudy, method = "ML"
)anova(sleep.random.intercept, sleep.random.coefficients) Model df AIC BIC logLik Test L.Ratio
sleep.random.intercept 1 4 1802.079 1814.851 -897.0393
sleep.random.coefficients 2 6 1763.939 1783.097 -875.9697 1 vs 2 42.1393
p-value
sleep.random.intercept
sleep.random.coefficients <.0001Wir haben beide Modelle geschätzt und sie danach mittels LR-Test verglichen (Signifikanztest für Slope-Varianz; auf die Berechnung des \(p\)-Wert mittels Mischverteilung verzichten wir hier). Es hat sich gezeigt, dass der Modell-Fit sich verbessert, wenn wir auch die Slopes als Random Effects modellieren, d.h. die Slope-Varianz ist signifikant. Daher sehen wir uns im Folgenden nur die Ergebnisse des Random-Coefficient-Modells im Detail an:
summary(sleep.random.coefficients)Linear mixed-effects model fit by maximum likelihood
Data: sleepstudy
AIC BIC logLik
1763.939 1783.097 -875.9697
Random effects:
Formula: ~Days | Subject
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 23.780376 (Intr)
Days 5.716807 0.081
Residual 25.591842
Fixed effects: Reaction ~ Days
Value Std.Error DF t-value p-value
(Intercept) 251.40510 6.669396 161 37.69533 0
Days 10.46729 1.510647 161 6.92901 0
Correlation:
(Intr)
Days -0.138
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.94156355 -0.46559311 0.02894656 0.46361051 5.17933587
Number of Observations: 180
Number of Groups: 18 Und wenn wir uns die Modell-Parameter anschauen, ist der Fixed-Effekt Parameter für Days (linearer Trend) signifikant, \(b_{Days} = 10.47, p < 0.001\). Wir können diesen Wert folgendermassen interpretieren: Jeder weitere Tag, an dem ein (zufällig ausgewählter) Lastwagenfahrer/Lastwagenfahrerin nur drei Stunden schläft, nimmt seine/ihre Reaktionszeit durchschnittlich um 10.47ms zu.
3. Kontrastmodelle
Wir möchten jetzt Days als Faktorvariable mit ins Modell nehmen. Das bedeutet, dass wir nicht mehr an einem linearen Effekt von Days interessiert sind. Stattdessen modellieren wir jeden einzelnen Tag separat. Dies ist flexibler, ein solches Modell benötigt aber mehr Parameter, was sich stark auf den Rechenaufwand für die Modellschätzung auswirkt (Schätzung braucht viel mehr Zeit).
Um den Prozess etwas abzukürzen, fassen wir die Daten ein wenig zusammen. Wir kreieren einen neuen Datenframe sleepstudy_f, der jeweils zwei Tage zusammenfasst. Insgesamt hat jede Person in sleepstudy_f nur noch fünf Einträge für Reaction, und zwar jeweils den Durchschnitt der ersten zwei Tage (Tag 0 und Tag 1), dann den Durchschnitt von Tag 2 und Tag 3, und so weiter.
Folgender Code-Chunk tut das für uns:
newdays <- paste(0:4 * 2, 1:5 * 2 - 1, sep = "-")[rep(1:5, each = 2)]
sleepstudy_f <- sleepstudy |>
mutate(Days_f = factor(
levels = c(newdays[1:5 * 2]),
rep(newdays, times = length(sleepstudy$Days) / 10)
)) |>
group_by(Subject, Days_f) |>
summarise(Reaction = mean(Reaction)) |>
ungroup()
levels(sleepstudy_f$Days_f)[1] "0-1" "2-3" "4-5" "6-7" "8-9"sleepstudy_f# A tibble: 90 × 3
Subject Days_f Reaction
<fct> <fct> <dbl>
1 308 0-1 214.
2 308 2-3 204.
3 308 4-5 212.
4 308 6-7 216.
5 308 8-9 231.
6 309 0-1 197.
7 309 2-3 234.
8 309 4-5 225.
9 309 6-7 246.
10 309 8-9 254.
# ℹ 80 more rowsJetzt ist die Variable Days_f bereits als Faktor gespeichert. Wir können sie also direkt verwenden.
# Hinzufügen der numerische Variable Days zum Datensatz
sleepstudy_f <- sleepstudy_f |>
mutate(Days = as.numeric(Days_f) - 1) |>
select(Subject, Days_f, Days, Reaction) # Reihenfolge anpassen
# Check...
sleepstudy_f# A tibble: 90 × 4
Subject Days_f Days Reaction
<fct> <fct> <dbl> <dbl>
1 308 0-1 0 214.
2 308 2-3 1 204.
3 308 4-5 2 212.
4 308 6-7 3 216.
5 308 8-9 4 231.
6 309 0-1 0 197.
7 309 2-3 1 234.
8 309 4-5 2 225.
9 309 6-7 3 246.
10 309 8-9 4 254.
# ℹ 80 more rows- Definieren Sie ein Random-Coefficients-Kontrast-Modell (mit
Days_fals Faktor)
Lösung
sleep.random.coefficients.contrast <- lme(Reaction ~ Days_f,
random = ~ Days_f | Subject,
sleepstudy_f, method = "ML",
control = list(opt = "optim", sigma = 1e-7)
)- Interpretieren Sie die Ergebnisse.
Lösung
summary(sleep.random.coefficients.contrast)Linear mixed-effects model fit by maximum likelihood
Data: sleepstudy_f
AIC BIC logLik
-1847.586 -1797.59 943.7931
Random effects:
Formula: ~Days_f | Subject
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 29.6864414 (Intr) Dy_2-3 Dy_4-5 Dy_6-7
Days_f2-3 24.8876950 -0.315
Days_f4-5 37.1239870 -0.141 0.638
Days_f6-7 46.7946065 -0.174 0.572 0.770
Days_f8-9 51.9289952 0.005 0.300 0.802 0.630
Residual 0.0000001
Fixed effects: Reaction ~ Days_f
Value Std.Error DF t-value p-value
(Intercept) 260.57378 7.200020 68 36.19070 0.0000
Days_f2-3 13.60317 6.036153 68 2.25362 0.0274
Days_f4-5 38.01016 9.003889 68 4.22153 0.0001
Days_f6-7 54.89064 11.349359 68 4.83645 0.0000
Days_f8-9 83.16658 12.594631 68 6.60334 0.0000
Correlation:
(Intr) Dy_2-3 Dy_4-5 Dy_6-7
Days_f2-3 -0.315
Days_f4-5 -0.141 0.638
Days_f6-7 -0.174 0.572 0.770
Days_f8-9 0.005 0.300 0.802 0.630
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.842171e-06 -1.136868e-06 -5.684342e-07 -5.684342e-07 0.000000e+00
Number of Observations: 90
Number of Groups: 18 Die Effekte von Days_f kontrastieren die Faktorstufen 2-3, 4-5, 6-7, 8-9 jeweils mit der Referenzkategorie 0-1. Diese Effekte (\(\hat\gamma_{10}= 13.6\), \(\hat\gamma_{20}= 38.01\), \(\hat\gamma_{30}= 54.89\), \(\hat\gamma_{40}= 83.17\)) sind allesamt signifikant und zeigen eine relativ gleichmässige Zunahme, was die Linearität des Zusammenhangs recht gut widerspiegelt.
Man kann sich das in etwa so vorstellen: Auf der Y-Achse ist jetzt die durchschnittliche Reaktionszeit mean_react pro Faktorstufe 1-5 dargestellt, beginnend mit dem Intercept des Modells (\(\hat\gamma_{00}= 260.57\)) für die erste Faktorstufe:
Und jetzt für die einzelnen Lastwagenfahrerinnen und Lastwagenfahrer (schwarze Linie mit Punkten). Zum Vergleich repräsentiert die dünne Linie den durchschnittlichen Verlauf.
Bates, Douglas M. 2010. Lme4: Mixed-Effects Modeling with R. Unpublished.
Belenky, Gregory, Nancy J. Wesensten, David R. Thorne, Maria L. Thomas, Helen C. Sing, Daniel P. Redmond, Michael B. Russo, und Thomas J. Balkin. 2003. „Patterns of Performance Degradation and Restoration during Sleep Restriction and Subsequent Recovery: A Sleep Dose-Response Study“. Journal of Sleep Research 12 (1): 1–12. https://doi.org/10.1046/j.1365-2869.2003.00337.x.
Eid, Michael, Mario Gollwitzer, und Manfred Schmitt. 2017. Statistik und Forschungsmethoden: mit Online-Materialien. 5., korrigierte Auflage. Weinheim Basel: Beltz.