pacman::p_load(tidyverse, ggplot2, ggthemes, haven, lavaan, semPlot, wesanderson)7 Strukturgleichungsmodelle (SEM)
7.1 Einführung
In dieser Übung soll vermittelt werden, wie mit lavaan Strukturgleichungsmodelle (SEM) definiert und berechnet werden können. SEM stellen eine Kombination aus CFA und Regressionsmodellen dar und ermöglichen es, komplexe Regressionsstrukturen (Pfadmodelle) auf der Ebene latenter Variablen zu modellieren. Dabei können auch indirekte Effekte (Mediationsmodelle) geschätzt werden. Die Schätztheorie unterscheidet sich nicht von derjenigen der CFA.
Mit einem Strukturgleichungsmodell wollen wir die Effekte der durch Jugendliche erlebten emotionalen Unterstützung durch Eltern und Freunde auf deren Lebenszufriedenheit untersuchen. Dabei sollen die beiden Selbstwirksamkeits-Komponenten “Akademische Selbstwirksamkeit” und “Soziale Selbstwirksamkeit” als Mediatoren dienen. Es sollen sowohl direkte als auch indirekte Effekte untersucht werden.
Inhaltliche Annahmen: Sowohl elterliche Unterstützung als auch Unterstützung durch Freunde haben einen positiven Effekt auf die Lebenszufriedenheit. Ausserdem ist aus der Selbstwirksamkeitsforschung bekannt, dass sich erfahrene Unterstützung positiv auf das Selbstwirksamkeitserleben auswirkt, und dass dieses wiederum mit Lebenszufriedenheit im Zusammenhang steht. Eine wichtige Frage ist jedoch, welche differentiellen Effekte sich zeigen, wenn man die Unterstützung aus zwei wichtigen sozialen Kontexten (Eltern und Freunde) und die beiden Selbstwirksamkeitsdomänen “akademisch” und “sozial” gleichzeitig betrachtet.
Zu dem postulierten Strukturmodell (Beziehungen zwischen den latenten Variablen) benötigen wir ein Messmodell (Beziehungen zwischen den latenten Variablen und den manifesten Variablen, also die Faktorenstruktur). In diesem Beispiel wurden die Konstrukte durch folgende manifeste Variablen gemessen:
Emotionale Unterstützung durch Eltern: unt_eltern1, unt_eltern2
Emotionale Unterstützung durch Freunde: unt_freunde1, unt_freunde2
Akademische Selbstwirksamkeit: swk_akad1, swk_akad2, swk_akad3, swk_akad4, swk_akad5
Soziale Selbstwirksamkeit: swk_soz1, swk_soz2, swk_soz3, swk_soz4
Lebenszufriedenheit: leben1, leben2, leben3
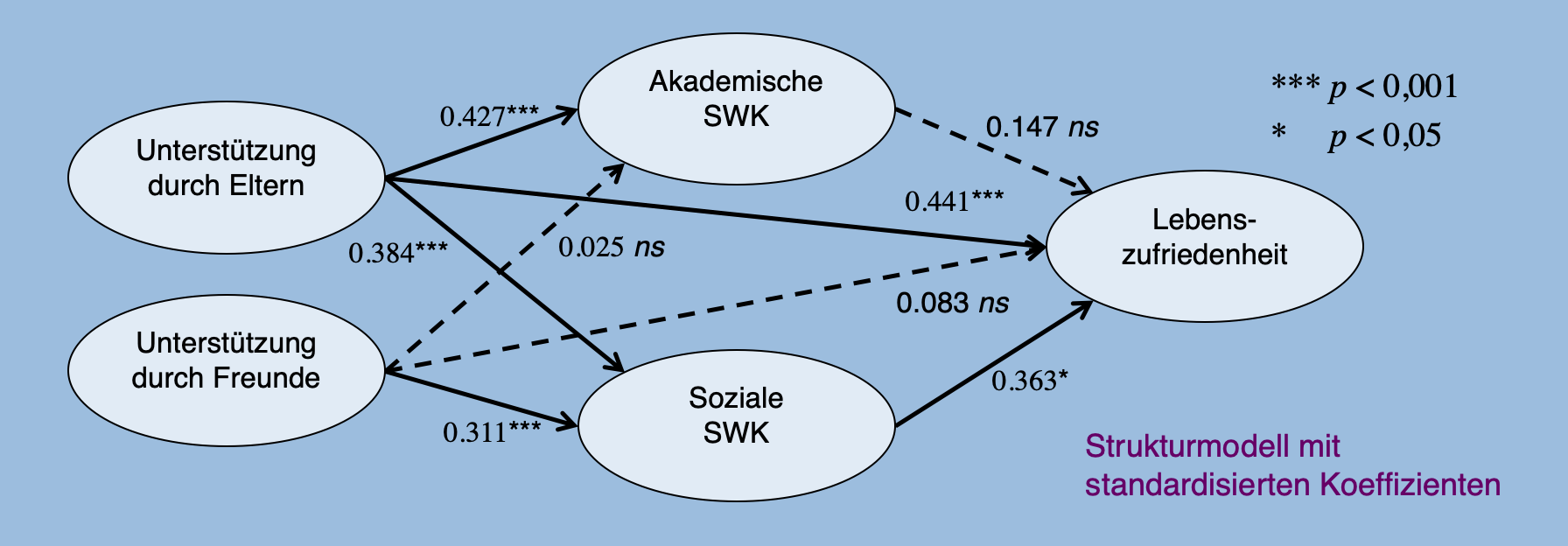
Die angenommenen Effekte lassen sich in folgendem Strukturmodell zusammenfassen:
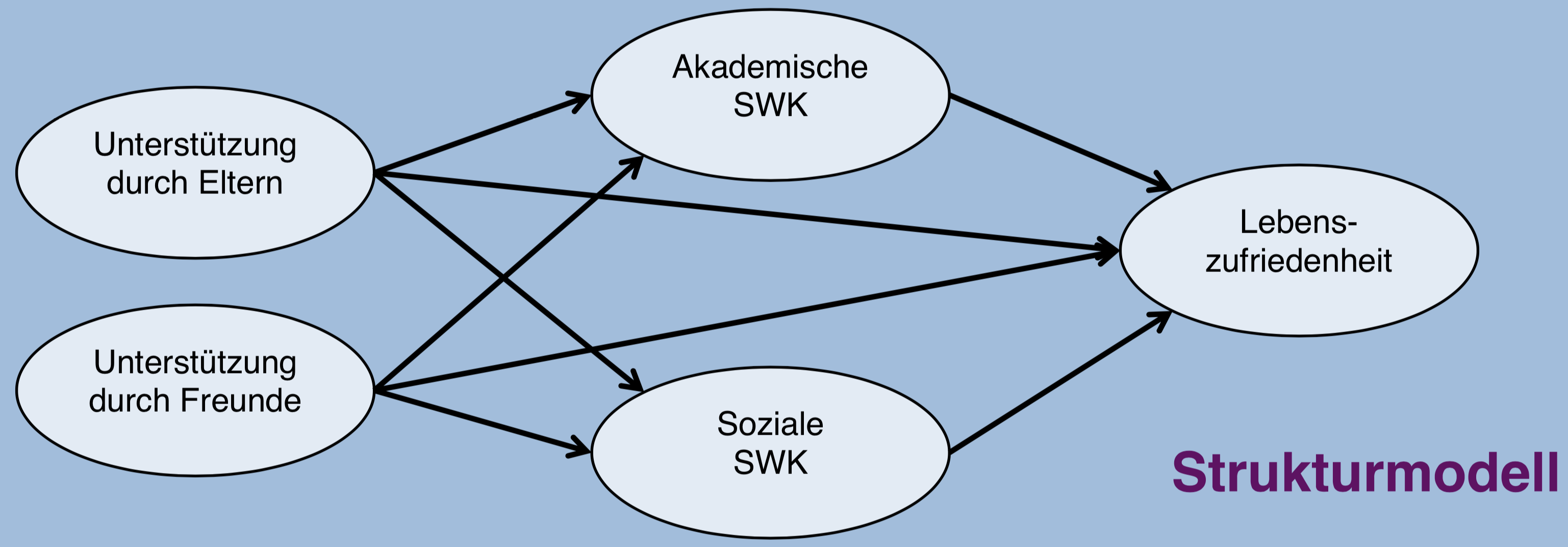 \(~\)
\(~\)
Wir werden die SEM-Analyse in drei Schritten vornehmen:
Zuerst wollen wir nur das Messmodell betrachten. Es handelt sich dabei um eine Multikonstrukt-CFA mit Interkorrelationen aller latenten Variablen.
Danach betrachten wir das gesamte Strukturgleichungsmodell (Messmodell und Strukturmodell zusammen).
Im letzten Schritt wollen wir zeigen, wie man innerhalb des Strukturgleichungsmodells explizit indirekte und totale Effekte definieren kann und wie man diese auf Signifikanz testet.
7.2 Packages laden und Datenimport
data <- read_csv("https://raw.githubusercontent.com/methodenlehre/data/master/statIV_sem/sem-data.csv")7.3 Messmodell
7.3.1 Modelldefinition
Im Messmodell werden die Zusammenhänge der latenten Variablen (Faktoren) mit den manifesten Variablen definiert. Die lavaan-Modelldefinition kennen wir bereits von der CFA.
Fehlervarianzen der beobachteten Variablen und Varianzen der exogenen latenten Variablen müssen nicht eigens spezifiziert werden
Operator für das Messmodell:
=~(“wird gemessen durch…”)
\(~\)
model_measurement <- "
# Messmodell
UNT_Eltern =~ unt_eltern1 + unt_eltern2
UNT_Freunde =~ unt_freunde1 + unt_freunde2
SWK_Akademisch =~ swk_akad1 + swk_akad2 + swk_akad3 + swk_akad4 + swk_akad5
SWK_Sozial =~ swk_soz1 + swk_soz2 + swk_soz3 + swk_soz4
ZUFRIEDEN =~ leben1 + leben2 + leben3
"\(~\)
Eigenschaften des Messmodells
Wie viele und welche manifesten Variablen hat das Modell?
16 manifeste Variablen (2 für UNT_Eltern, 2 für UNT_Freunde, 5 für SWK_Akademisch, 4 für SWK_Sozial, 3 für ZUFRIEDEN)
Wie viele Informationen enthält die Varianz-Kovarianz-Matrix der manifesten Variablen?
\((16 \cdot 17) / 2 = 136\)
Wie viele und welche Parameter müssen geschätzt werden?
11 Faktorladungen (eine für jede manifeste Variable minus Anzahl latenter Variablen, da die erste Ladung jeweils auf 1 fixiert wird)
16 Residualvarianzen der manifesten Variablen
5 Varianzen der latenten Variablen
10 Kovarianzen der latenten Variablen
Wie viele Freiheitsgrade besitzt das Modell?
\(df = 136 - (11 + 16 + 5 + 10) = 136 - 42 = 94\)
\(~\)
7.3.2 Modellschätzung
Die Funktion sem() wird auf das oben spezifizierte Modell model_measurement angewendet, die Ergebnisse werden in einem Objekt (hier mit dem beliebigen Namen fit_measurement) gespeichert. Man könnte hier auch cfa() verwenden. Die beiden Funktionen unterscheiden sich nur geringfügig in ihren Default-Einstellungen und sind beide gleichermassen für die Schätzung von Messmodellen geeignet.
fit_measurement <- sem(model_measurement,
data = data
)
summary(fit_measurement,
fit.measures = TRUE,
standardized = TRUE
)lavaan 0.6-21 ended normally after 62 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 42
Used Total
Number of observations 262 265
Model Test User Model:
Test statistic 288.018
Degrees of freedom 94
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 2247.066
Degrees of freedom 120
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.909
Tucker-Lewis Index (TLI) 0.884
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -4040.188
Loglikelihood unrestricted model (H1) -3896.179
Akaike (AIC) 8164.376
Bayesian (BIC) 8314.247
Sample-size adjusted Bayesian (SABIC) 8181.088
Root Mean Square Error of Approximation:
RMSEA 0.089
90 Percent confidence interval - lower 0.077
90 Percent confidence interval - upper 0.101
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.895
Standardized Root Mean Square Residual:
SRMR 0.061
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
UNT_Eltern =~
unt_eltern1 1.000 0.773 0.902
unt_eltern2 1.052 0.088 11.961 0.000 0.813 0.830
UNT_Freunde =~
unt_freunde1 1.000 0.756 0.759
unt_freunde2 1.081 0.146 7.405 0.000 0.817 1.004
SWK_Akademisch =~
swk_akad1 1.000 0.687 0.774
swk_akad2 0.779 0.070 11.118 0.000 0.535 0.689
swk_akad3 0.940 0.072 13.054 0.000 0.646 0.797
swk_akad4 0.871 0.072 12.032 0.000 0.599 0.740
swk_akad5 0.888 0.073 12.247 0.000 0.610 0.752
SWK_Sozial =~
swk_soz1 1.000 0.543 0.786
swk_soz2 1.146 0.088 13.070 0.000 0.623 0.794
swk_soz3 0.884 0.071 12.474 0.000 0.480 0.760
swk_soz4 1.094 0.093 11.766 0.000 0.594 0.722
ZUFRIEDEN =~
leben1 1.000 0.396 0.464
leben2 1.233 0.178 6.944 0.000 0.488 0.788
leben3 1.500 0.218 6.891 0.000 0.594 0.766
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
UNT_Eltern ~~
UNT_Freunde 0.098 0.041 2.364 0.018 0.167 0.167
SWK_Akademisch 0.229 0.042 5.403 0.000 0.431 0.431
SWK_Sozial 0.183 0.034 5.438 0.000 0.436 0.436
ZUFRIEDEN 0.207 0.038 5.501 0.000 0.677 0.677
UNT_Freunde ~~
SWK_Akademisch 0.050 0.035 1.418 0.156 0.096 0.096
SWK_Sozial 0.154 0.036 4.223 0.000 0.376 0.376
ZUFRIEDEN 0.092 0.028 3.320 0.001 0.307 0.307
SWK_Akademisch ~~
SWK_Sozial 0.243 0.035 6.981 0.000 0.651 0.651
ZUFRIEDEN 0.158 0.031 5.059 0.000 0.582 0.582
SWK_Sozial ~~
ZUFRIEDEN 0.147 0.027 5.390 0.000 0.682 0.682
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.unt_eltern1 0.136 0.043 3.170 0.002 0.136 0.186
.unt_eltern2 0.300 0.053 5.685 0.000 0.300 0.312
.unt_freunde1 0.420 0.080 5.260 0.000 0.420 0.424
.unt_freunde2 -0.005 0.083 -0.059 0.953 -0.005 -0.007
.swk_akad1 0.316 0.035 9.090 0.000 0.316 0.401
.swk_akad2 0.317 0.032 10.032 0.000 0.317 0.525
.swk_akad3 0.239 0.028 8.696 0.000 0.239 0.364
.swk_akad4 0.296 0.031 9.546 0.000 0.296 0.452
.swk_akad5 0.286 0.030 9.402 0.000 0.286 0.435
.swk_soz1 0.183 0.021 8.721 0.000 0.183 0.382
.swk_soz2 0.228 0.027 8.578 0.000 0.228 0.370
.swk_soz3 0.168 0.018 9.145 0.000 0.168 0.422
.swk_soz4 0.325 0.034 9.630 0.000 0.325 0.479
.leben1 0.572 0.053 10.793 0.000 0.572 0.785
.leben2 0.146 0.020 7.281 0.000 0.146 0.379
.leben3 0.249 0.032 7.858 0.000 0.249 0.414
UNT_Eltern 0.597 0.075 7.930 0.000 1.000 1.000
UNT_Freunde 0.571 0.106 5.399 0.000 1.000 1.000
SWK_Akademisch 0.472 0.066 7.100 0.000 1.000 1.000
SWK_Sozial 0.295 0.041 7.219 0.000 1.000 1.000
ZUFRIEDEN 0.157 0.043 3.630 0.000 1.000 1.0007.3.3 Darstellung als Pfaddiagramm
Hier soll auch gezeigt werden, wie mit semPaths() aus dem Package semTools Pfaddiagramme aus den gefitteten lavaan-Objekten generiert werden können. Wir lassen uns das Modell mit den standardisierten Parameter Estimates mit layout = 'spring' darstellen.
# Wir können schon jetzt die Farben für semPaths definieren, nämlich als Liste
# mit den Farb-Parametern für manifeste (man) und latente (lat) Variablen.
cols <- wes_palette(
name = "Moonrise2",
n = 4,
type = "discrete"
)
colorlist <- list(
man = cols[2],
lat = cols[3]
)
semPaths(fit_measurement,
what = "col", # Gleichmässige Pfade
whatLabels = "std", # Standardisierte Werte
style = "mx",
color = colorlist,
rotation = 1,
layout = "tree", # Layout der Darstellung
nCharNodes = 7, # Anzahl Buchstaben pro Variable (Abkürzung)
shapeMan = "rectangle", # Form der manifesten Variable
sizeMan = 8, # Breite der manifesten Variablen
sizeMan2 = 5
) # Höhe der manifesten Variablen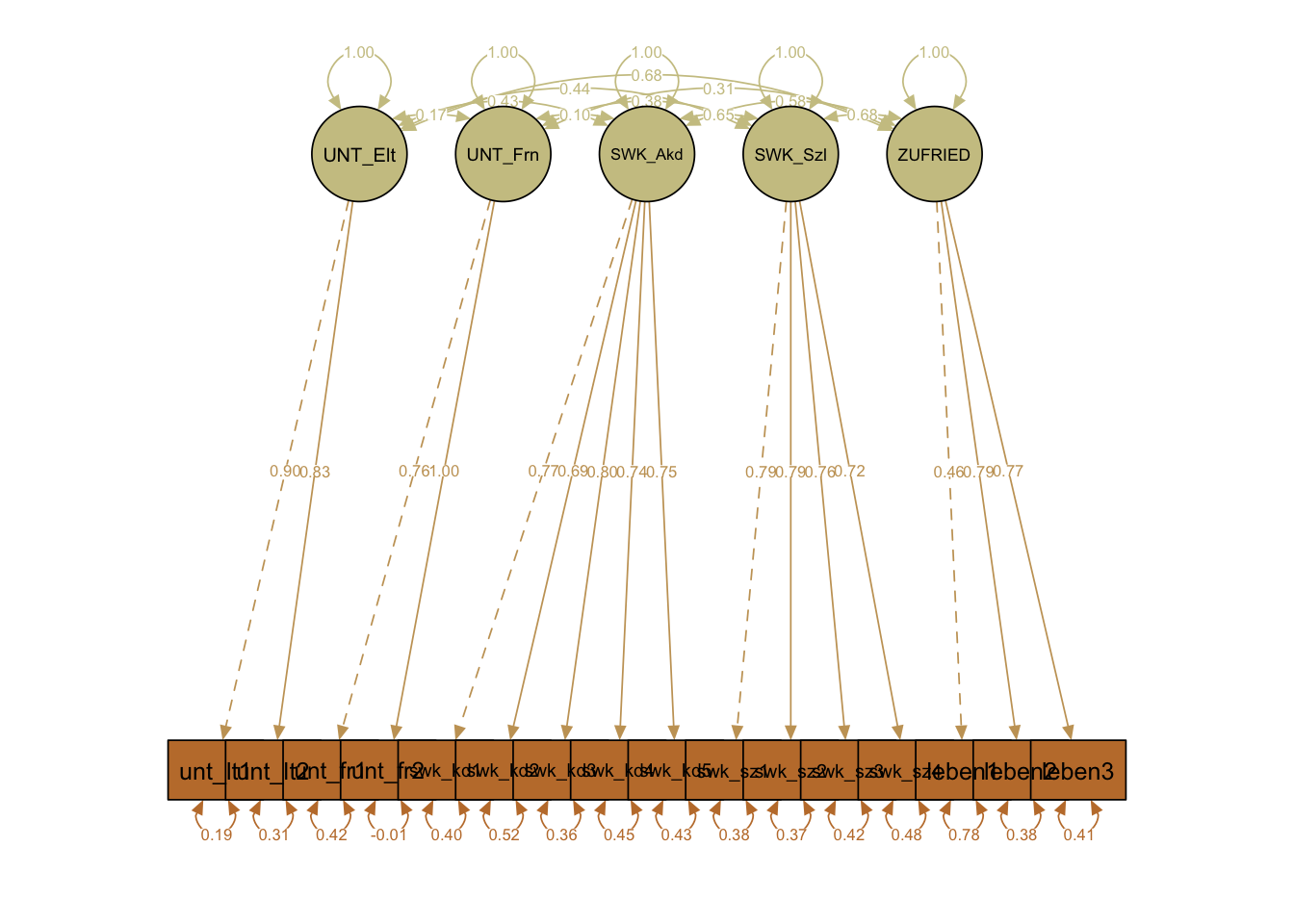
7.3.4 Modell-Fit
Wie aus dem summary()-Output und der graphischen Darstellung ersichtlich, sind die standardisierten Ladungen der manifesten Variablen auf den Faktoren alle relativ hoch und auch homogen. Die Faktor-Korrelationen dieses Multikonstrukt-Messmodells liegen zwischen \(r = 0.096\) (UNT_Freunde \(\leftrightarrow\) SWK_Akademisch) und \(r = 0.682\) (SWK_Sozial \(\leftrightarrow\) ZUFRIEDEN).
Die globale Modellpassung ist mit CFI = 0.909, NNFI/TLI = 0.884, RMSEA = 0.089 (90 %-CI: [0.077; 0.101]) nicht wirklich gut, kann aber nach den gängigen Kriterien als gerade noch akzeptabel bezeichnet werden.
Um festzustellen, wo Probleme in der Modellpassung bestehen, können wir zum einen die standardisierte Residual-Varianz-Kovarianz-Matrix betrachten:
resid(fit_measurement,
type = "standardized"
)$cov unt_l1 unt_l2 unt_f1 unt_f2 swk_k1 swk_k2 swk_k3 swk_k4 swk_k5
unt_eltern1 0.000
unt_eltern2 0.000 0.000
unt_freunde1 -0.474 -0.709 0.000
unt_freunde2 0.057 -0.089 0.000 0.000
swk_akad1 -1.768 -2.728 0.460 -1.627 0.000
swk_akad2 1.293 1.301 1.802 0.446 -0.586 0.000
swk_akad3 1.350 -0.127 0.585 -0.009 1.178 -0.594 0.000
swk_akad4 -0.255 -0.690 2.783 0.838 -0.155 -0.807 1.672 0.000
swk_akad5 0.814 0.468 -0.140 0.576 0.075 2.525 -1.125 -3.025 0.000
swk_soz1 0.527 -0.737 1.612 0.100 -0.188 0.667 0.177 3.558 2.190
swk_soz2 1.531 1.755 0.521 0.056 -0.339 -2.528 -1.886 3.789 1.447
swk_soz3 -1.629 -0.105 2.205 2.661 -1.131 -3.023 -1.318 -0.172 -1.587
swk_soz4 -1.195 -0.462 -2.385 -3.193 1.279 -1.954 -1.731 1.369 0.714
leben1 -0.717 -1.193 -1.280 0.972 -2.441 -1.455 -2.085 -2.858 -1.060
leben2 -5.017 -4.083 3.097 3.955 -0.934 0.926 -0.118 -1.326 1.309
leben3 4.735 4.796 -1.702 -4.460 -0.506 3.922 -0.162 0.350 1.800
swk_s1 swk_s2 swk_s3 swk_s4 leben1 leben2 leben3
unt_eltern1
unt_eltern2
unt_freunde1
unt_freunde2
swk_akad1
swk_akad2
swk_akad3
swk_akad4
swk_akad5
swk_soz1 0.000
swk_soz2 0.028 0.000
swk_soz3 -1.839 -0.046 0.000
swk_soz4 -1.251 0.017 2.790 0.000
leben1 1.733 0.979 2.644 2.321 0.000
leben2 2.835 1.249 2.497 1.516 0.836 0.000
leben3 -0.539 -2.619 -5.345 -2.875 -0.875 -0.021 0.000Hier zeigt sich, dass die vom Modell implizierte Varianz-Kovarianz-Matrix an vielen Stellen des Modells signifikant von der empirischen Varianz-Kovarianz-Matrix abweicht. Eine Häufung sehr hoher standardisierter Residual-Kovarianzen zeigt sich z.B. bezüglich der manifesten Variablen leben3.
Eine weitere Möglichkeit zur lokalen Fit-Diagnostik bieten die Modell-Modifikationsindizes. Diese zeigen an, bei welchen zusätzlichen zu schätzenden Modellparametern sich eine deutliche Fit-Verbesserung ergeben würde (im Sinne einer Reduktion von \(\chi^2\) um den Wert des entsprechenden MI). Wir lassen uns hier nur die MI \(\geq 5\) ausgeben, da üblicherweise nur solche als substantiell angesehen werden.
modindices(fit_measurement,
standardized = FALSE,
minimum.value = 5
) lhs op rhs mi epc
50 UNT_Eltern =~ swk_akad1 6.363 -0.159
60 UNT_Eltern =~ leben2 31.249 -0.454
61 UNT_Eltern =~ leben3 39.880 0.628
71 UNT_Freunde =~ swk_soz3 7.365 0.114
72 UNT_Freunde =~ swk_soz4 9.594 -0.175
74 UNT_Freunde =~ leben2 16.164 0.190
75 UNT_Freunde =~ leben3 21.393 -0.268
80 SWK_Akademisch =~ swk_soz1 5.215 0.166
82 SWK_Akademisch =~ swk_soz3 7.140 -0.180
84 SWK_Akademisch =~ leben1 6.835 -0.268
94 SWK_Sozial =~ swk_akad4 10.514 0.351
97 SWK_Sozial =~ leben2 21.031 0.556
98 SWK_Sozial =~ leben3 36.446 -0.895
145 unt_freunde1 ~~ swk_akad4 8.497 0.069
146 unt_freunde1 ~~ swk_akad5 6.802 -0.061
151 unt_freunde1 ~~ leben1 9.867 -0.097
165 unt_freunde2 ~~ leben3 5.650 -0.046
173 swk_akad1 ~~ swk_soz4 6.213 0.059
179 swk_akad2 ~~ swk_akad5 7.603 0.064
181 swk_akad2 ~~ swk_soz2 6.587 -0.051
186 swk_akad2 ~~ leben3 16.436 0.086
196 swk_akad4 ~~ swk_akad5 7.637 -0.065
198 swk_akad4 ~~ swk_soz2 13.384 0.072
222 swk_soz3 ~~ swk_soz4 9.801 0.060
223 swk_soz3 ~~ leben1 7.223 0.058
224 swk_soz3 ~~ leben2 6.919 0.034
225 swk_soz3 ~~ leben3 23.662 -0.079\(~\)
Es werden insgesamt 24 Modifikationsindizes ausgegeben. Sie beziehen sich entweder auf mögliche Querladungen (z.B. UNT_Eltern =~ leben3: MI = 39.880) oder auf Residualkovarianzen zwischen manifesten Variablen (z.B. unt_freunde1 ~~ swk_akad4: MI = 8.497). Im Sinne unseres theoretischen Modells (bestimmte inhaltlich definierte Items messen bestimmte latente Konstrukte) ist die Hinzufügung von Querladungen und Residualkovarianzen nicht sinnvoll.
Solche Model-Fit-Probleme ergeben sich nicht selten bei Self-Report-Studien. Beim Antworten auf Likert-Skalen bestehen oft individuelle Unterschiede in der Skalennutzung (sog. Antwortstile oder Response Styles). Diese können zu generell erhöhten Korrelationen der Variablen untereinander führen, die ggf. in einem Multikonstrukt-Messmodell keine angemessene Berücksichtigung finden können. Es gibt hierzu Lösungsansätze (Definition von Methoden- und Response-Style-Faktoren), die wir hier aber nicht weiter vertiefen.
Ein weiterer Grund für die Model-Fit Probleme in dieser Studie könnte die allgemeine Ähnlichkeit der untersuchten Konstrukte in Bezug auf die dort erfragten Lebensbereiche sein. Beispielsweise enthalten die Lebenszufriedenheits-Items solche zum Bereich “Freunde”, der Freunde-Kontext spielt aber auch bei den Items zur sozialen Selbstwirksamkeit und natürlich beim denen zur Unterstützung durch Freunde eine grosse Rolle.
Da der Model-Fit noch akzeptabel ist, arbeiten wir mit diesem Messmodell weiter und wollen im nächsten Schritt die unseren inhaltlichen Hypothesen entsprechenden Effekte zwischen den latenten Variablen modellieren (Strukturmodell).
7.4 Gesamtmodell
7.4.1 Modelldefinition
Zusätzlich zum Messmodell wird im Gesamtmodell auch das Strukturmodell definiert. Das Strukturmodell repräsentiert die Zusammenhänge/Effekte zwischen den latenten Variablen.
model <- "
# Messmodell
UNT_Eltern =~ unt_eltern1 + unt_eltern2
UNT_Freunde =~ unt_freunde1 + unt_freunde2
SWK_Akademisch =~ swk_akad1 + swk_akad2 + swk_akad3 + swk_akad4 + swk_akad5
SWK_Sozial =~ swk_soz1 + swk_soz2 + swk_soz3 + swk_soz4
ZUFRIEDEN =~ leben1 + leben2 + leben3
# Strukturmodell
# Regressionsgleichungen
SWK_Akademisch ~ UNT_Eltern + UNT_Freunde
SWK_Sozial ~ UNT_Eltern + UNT_Freunde
ZUFRIEDEN ~ SWK_Akademisch + SWK_Sozial + UNT_Eltern + UNT_Freunde
# Residual-Kovarianzen
SWK_Akademisch ~~ SWK_Sozial
"Operator für das Strukturmodell (Regressionen latenter Variablen):
~(“wird vorhergesagt durch…”)Operator für (Residual-)Varianzen und Kovarianzen:
~~(bei Varianzen steht links und rechts dieselbe Variable, bei Kovarianzen unterschiedliche). Wie schon im Messmodell (CFA) müssen Varianzen und Kovarianzen exogener latenter Variablen nicht angegeben werden (werden automatisch geschätzt). Auch die Residualvarianzen endogener latenter Variablen werden automatisch geschätzt.
Wir müssen daher nur einen Parameter mit ~~ spezifizieren: In diesem Modell haben wir zwei parallele latente Mediatorvariablen (SWK_Akademisch und SWK_Sozial), die keinerlei Effekte aufeinander haben. Es ist aber anzunehmen, dass diese beiden Variablen kovariieren (vgl. auch die Korrelation von \(r=0.651\) im Messmodell oben), da neben den bereichsspezifischen Selbstwirksamkeiten auch eine übergeordnete allgemeine Selbstwirksamkeit angenommen werden kann (vgl. auch die CFA zur Lebenszufriedenheit). Da es sich bei SWK_Akademisch und SWK_Sozial um endogene latente Variablen handelt (beide werden sowohl von UNT_Eltern als auch von UNT_Freunde vorhergesagt), muss hier eine Residualkovarianz \(\psi =\) SWK_Akademisch ~~ SWK_Sozial spezifiziert werden.
Eigenschaften des Gesamtmodells
Wie viele und welche manifesten Variablen hat das Modell?
16 manifeste Variablen (2 für UNT_Eltern, 2 für UNT_Freunde, 5 für SWK_Akademisch, 4 für SWK_Sozial, 3 für ZUFRIEDEN)
Wie viele Informationen enthält die Varianz-Kovarianz-Matrix der manifesten Variablen?
\((16 \cdot 17) / 2 = 136\)
Wie viele und welche Parameter müssen geschätzt werden?
11 Faktorladungen (eine für jede manifeste Variable minus Anzahl latenter Variablen, da die erste Ladung jeweils auf 1 fixiert wird)
16 Residualvarianzen der manifesten Variablen
8 Strukturpfade
2 Varianzen der exogenen latenten Variablen
1 Kovarianz der beiden exogenen latenten Variablen
3 Residualvarianzen der endogenen latenten Variablen
1 Residualkovarianz der beiden endogenen latenten Variablen SWK_Akademisch und SWK_Sozial
Wie viele Freiheitsgrade besitzt das Modell?
\(df = 136 - (11 + 16 + 8 + 2 + 1 + 3 + 1) = 136 - 42 = 94\)
\(~\)
7.4.2 Modellschätzung
fit <- sem(model,
data = data
)
summary(fit,
fit.measures = TRUE,
standardized = TRUE
)lavaan 0.6-21 ended normally after 53 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 42
Used Total
Number of observations 262 265
Model Test User Model:
Test statistic 288.018
Degrees of freedom 94
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 2247.066
Degrees of freedom 120
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.909
Tucker-Lewis Index (TLI) 0.884
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -4040.188
Loglikelihood unrestricted model (H1) -3896.179
Akaike (AIC) 8164.376
Bayesian (BIC) 8314.247
Sample-size adjusted Bayesian (SABIC) 8181.088
Root Mean Square Error of Approximation:
RMSEA 0.089
90 Percent confidence interval - lower 0.077
90 Percent confidence interval - upper 0.101
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.895
Standardized Root Mean Square Residual:
SRMR 0.061
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
UNT_Eltern =~
unt_eltern1 1.000 0.773 0.902
unt_eltern2 1.052 0.088 11.961 0.000 0.813 0.830
UNT_Freunde =~
unt_freunde1 1.000 0.756 0.759
unt_freunde2 1.081 0.146 7.405 0.000 0.817 1.004
SWK_Akademisch =~
swk_akad1 1.000 0.687 0.774
swk_akad2 0.779 0.070 11.118 0.000 0.535 0.689
swk_akad3 0.940 0.072 13.054 0.000 0.646 0.797
swk_akad4 0.871 0.072 12.032 0.000 0.599 0.740
swk_akad5 0.888 0.073 12.247 0.000 0.610 0.752
SWK_Sozial =~
swk_soz1 1.000 0.543 0.786
swk_soz2 1.146 0.088 13.070 0.000 0.623 0.794
swk_soz3 0.884 0.071 12.474 0.000 0.480 0.760
swk_soz4 1.094 0.093 11.766 0.000 0.594 0.722
ZUFRIEDEN =~
leben1 1.000 0.396 0.464
leben2 1.233 0.178 6.944 0.000 0.488 0.788
leben3 1.500 0.218 6.891 0.000 0.594 0.766
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
SWK_Akademisch ~
UNT_Eltern 0.379 0.065 5.797 0.000 0.427 0.427
UNT_Freunde 0.022 0.057 0.395 0.693 0.025 0.025
SWK_Sozial ~
UNT_Eltern 0.270 0.049 5.502 0.000 0.384 0.384
UNT_Freunde 0.224 0.046 4.892 0.000 0.311 0.311
ZUFRIEDEN ~
SWK_Akademisch 0.085 0.051 1.671 0.095 0.147 0.147
SWK_Sozial 0.265 0.077 3.439 0.001 0.363 0.363
UNT_Eltern 0.226 0.046 4.934 0.000 0.441 0.441
UNT_Freunde 0.043 0.032 1.373 0.170 0.083 0.083
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.SWK_Akademisch ~~
.SWK_Sozial 0.170 0.027 6.265 0.000 0.598 0.598
UNT_Eltern ~~
UNT_Freunde 0.098 0.041 2.364 0.018 0.167 0.167
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.unt_eltern1 0.136 0.043 3.170 0.002 0.136 0.186
.unt_eltern2 0.300 0.053 5.685 0.000 0.300 0.312
.unt_freunde1 0.420 0.080 5.260 0.000 0.420 0.424
.unt_freunde2 -0.005 0.083 -0.059 0.953 -0.005 -0.007
.swk_akad1 0.316 0.035 9.090 0.000 0.316 0.401
.swk_akad2 0.317 0.032 10.032 0.000 0.317 0.525
.swk_akad3 0.239 0.028 8.696 0.000 0.239 0.364
.swk_akad4 0.296 0.031 9.546 0.000 0.296 0.452
.swk_akad5 0.286 0.030 9.402 0.000 0.286 0.435
.swk_soz1 0.183 0.021 8.721 0.000 0.183 0.382
.swk_soz2 0.228 0.027 8.578 0.000 0.228 0.370
.swk_soz3 0.168 0.018 9.145 0.000 0.168 0.422
.swk_soz4 0.325 0.034 9.630 0.000 0.325 0.479
.leben1 0.572 0.053 10.793 0.000 0.572 0.785
.leben2 0.146 0.020 7.281 0.000 0.146 0.379
.leben3 0.249 0.032 7.858 0.000 0.249 0.414
UNT_Eltern 0.597 0.075 7.930 0.000 1.000 1.000
UNT_Freunde 0.571 0.106 5.399 0.000 1.000 1.000
.SWK_Akademisch 0.384 0.056 6.879 0.000 0.814 0.814
.SWK_Sozial 0.211 0.031 6.827 0.000 0.715 0.715
.ZUFRIEDEN 0.054 0.017 3.220 0.001 0.343 0.3437.4.3 Modell-Fit
Der Model Fit ist genau gleich geblieben! Wir haben schon oben gesehen, dass wir im Gesamtmodell genauso viele Parameter und damit Freiheitsgrade haben wie im Messmodell.
Das bedeutet, dass das Strukturmodell saturiert ist!
Im Messmodell hatten wir 15 Varianz- und Kovarianzparameter der latenten Variablen, somit war die Varianz-Kovarianzmatrix der latenten Variablen (mit 5*6/2 = 15 Elementen) vollständig und unrestringiert. Im Strukturmodell haben wir nun auch 15 Parameter. Die Parameter des Strukturmodells sind zwar schätzbar und wir können somit unsere postulierten Effekte überprüfen, aber dieser Teil des Gesamtmodells ist gerade so identifiziert (weil in Bezug auf die latenten Variablen gilt: \(n_{Info} = n_{Par}\)) und trägt damit nichts zur Überprüfung des Model Fits des Gesamtmodells bei! Anders ausgedrückt: Wir können nicht überprüfen, ob das Strukturmodell gut auf unsere Daten passt, nur der Fit des Messmodells ist überprüfbar.
Interpretation der geschätzten Strukturkoeffizienten:
Von den 8 postulierten Strukturpfaden sind 5 signifikant und gehen in die erwartete Richtung. Nicht signifikant sind die Effekte von UNT_Freunde auf SWK_Akademisch (Std.all \(= 0.025,\ p = 0.693\)), von UNT_Freunde auf ZUFRIEDEN (Std.all \(= 0.083,\ p = 0.170\)) und von SWK_Akademisch auf ZUFRIEDEN (Std.all \(= 0.147,\ p = 0.095\)).
Besonders auffällig ist, dass die wahrgenommene Unterstützung durch die Eltern einen substantiellen direkten Effekt auf die Zufriedenheit hat, während der direkte Effekt der wahrgenommenen Unterstützung durch die Freunde nicht signifikant war. Zudem erstaunt, dass die soziale Selbstwirksamkeit einen direkten Einfluss auf die Zufriedenheit hat, aber dass die akademische Selbstwirksamkeit keinen signifikanten direkten Einfluss auf die Zufriedenheit hat.
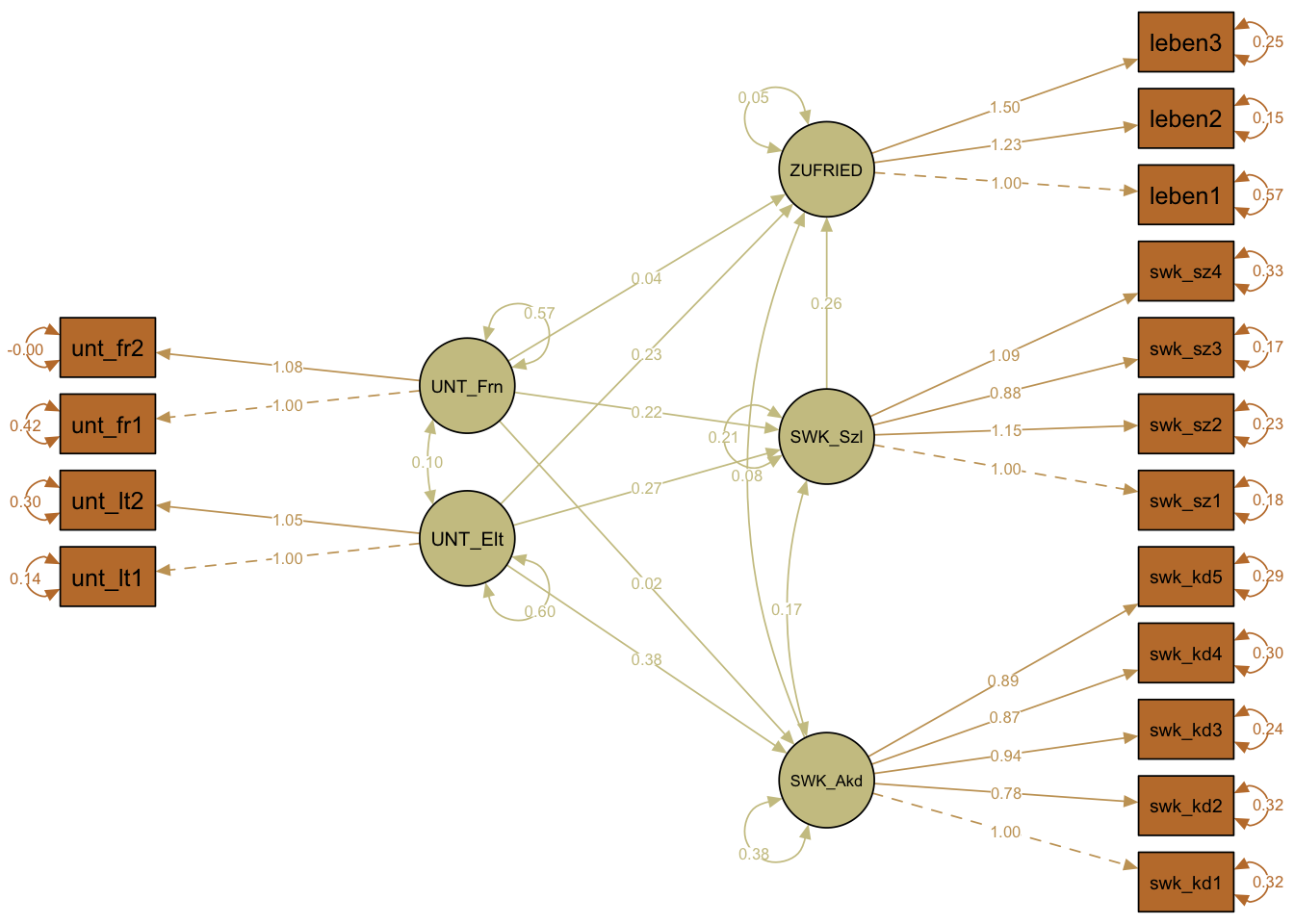
7.4.4 Darstellung als Pfaddiagramm
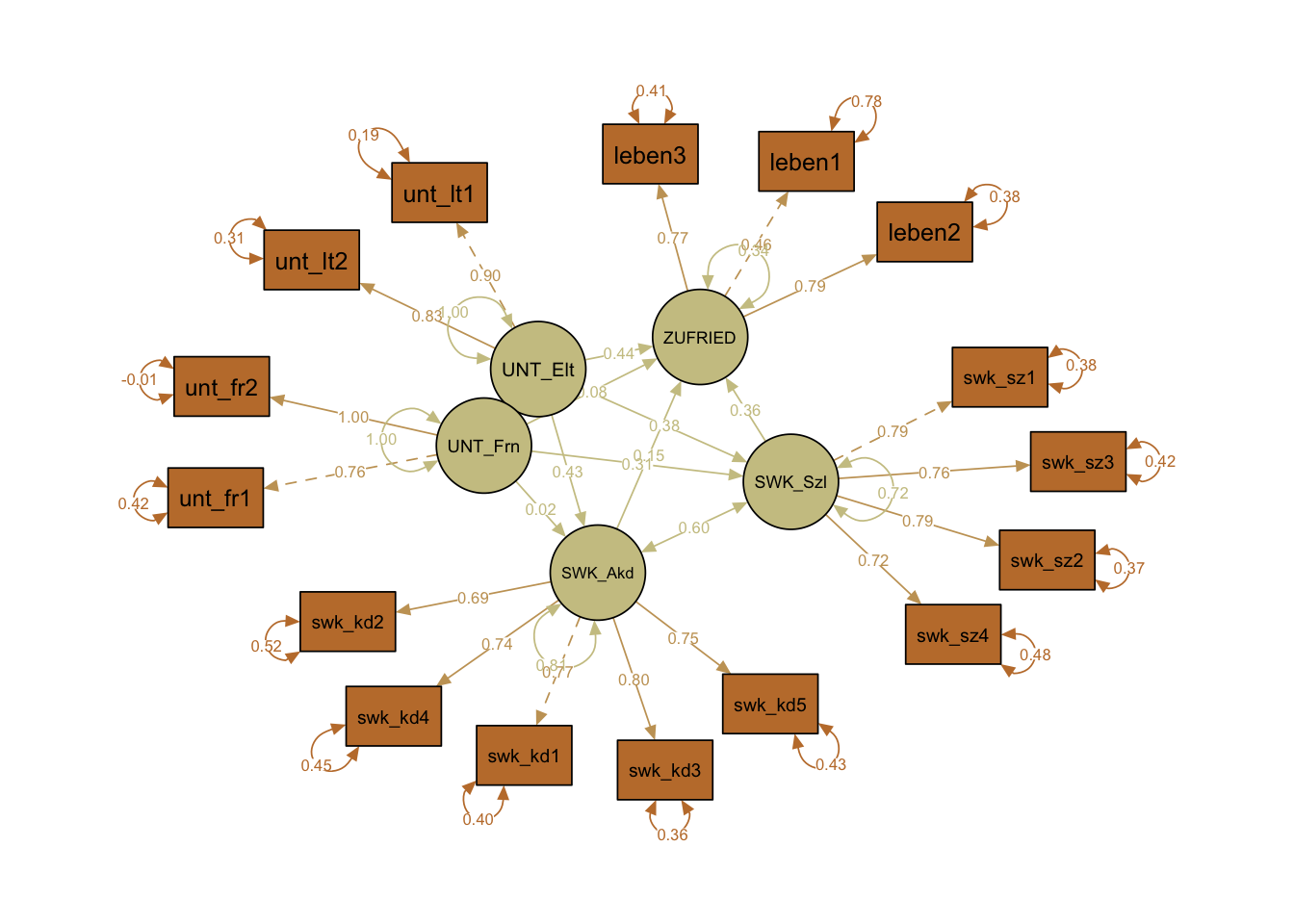
Wir lassen uns das Modell jetzt auf zwei verschiedene Arten darstellen, einmal mit den unstandardisierten Parameter Estimates (whatLabels = "par") mit layout = 'tree2' und einmal mit den standardisierten Parameter Estimates (whatLabels = "std") mit layout = 'spring'.
semPaths(fit,
what = "col",
whatLabels = "par",
style = "mx",
color = colorlist,
rotation = 2,
layout = "tree2",
mar = c(1, 2, 1, 2),
nCharNodes = 7,
shapeMan = "rectangle",
sizeMan = 8,
sizeMan2 = 5
)
semPaths(fit,
what = "col",
whatLabels = "std",
style = "mx",
color = colorlist,
rotation = 1,
layout = "spring",
nCharNodes = 7,
shapeMan = "rectangle",
sizeMan = 8,
sizeMan2 = 5
)
7.4.5 Berechnung indirekter und totaler Effekte
Alle Berechnungen sollen mit den standardisierten Estimates (Std.all) durchgeführt werden!
Spezifische indirekte Effekte
1. UNT_Eltern \(\rightarrow\) SWK_Akademisch \(\rightarrow\) ZUFRIEDEN:
\(0.427 \cdot 0.147 = 0.063\)
2. UNT_Eltern \(\rightarrow\) SWK_Sozial \(\rightarrow\) ZUFRIEDEN:
\(0.384 \cdot 0.363 = 0.139\)
3. UNT_Freunde \(\rightarrow\) SWK_Akademisch \(\rightarrow\) ZUFRIEDEN:
\(0.025 \cdot 0.147 = 0.004\)
4. UNT_Freunde \(\rightarrow\) SWK_Sozial \(\rightarrow\) ZUFRIEDEN:
\(0.311 \cdot 0.363 = 0.113\)
\(~\)
Totale indirekte Effekte
1. UNT_Eltern \(\rightarrow\) ZUFRIEDEN über SWK_Akademisch und SWK_Sozial:
\(0.427 \cdot 0.147 + 0.384 \cdot 0.363 = 0.202\)
2. UNT_Freunde \(\rightarrow\) ZUFRIEDEN über SWK_Akademisch und SWK_Sozial:
\(0.025 \cdot 0.147 + 0.311 \cdot 0.363 = 0.117\)
\(~\)
Totale Effekte
1. UNT_Eltern \(\rightarrow\) ZUFRIEDEN:
\(0.427 \cdot 0.147 + 0.384 \cdot 0.363 + 0.441 = 0.643\)
2. UNT_Freunde \(\rightarrow\) ZUFRIEDEN:
\(0.025 \cdot 0.147 + 0.311 \cdot 0.363 + 0.083 = 0.200\)
Wir können indirekte und totale Effekte auch in lavaan schätzen lassen und dort dann auch Signifikanztests für diese erhalten. Das ist unser letzter Schritt in der Analyse des vorliegenden Strukturgleichungsmodells.
7.5 Testung indirekter und totaler Effekte
Sobald im Strukturmodell eine oder mehrere latente Mediatorvariablen (d.h. solche, die sowohl Prädiktor als auch Prädikand anderer latenter Variablen sind) vorhanden sind, handelt es sich um eine Mediationsanalyse. Um indirekte und totale Effekte zu schätzen, müssen die Parameter des Strukturmodells zuerst in der Modelldefinition benannt werden (Vormultiplikation mit b1, b2, b3 usw.)
Spezifische (und ggf. totale) indirekte Effekte können dann als Produkte (bzw. Summe der Produkte) der Pfadparameter definiert werden (Operator:
:=)Totale Effekte können gleichermassen als Summe von indirekten und direkten Effekten definiert werden.
Die Schätzung (und Testung) indirekter und totaler Effekte sollte mit der Option se = "bootstrap" durchgeführt werden, da ein Produkt zweier (oder mehrerer) Pfadkoeffizienten nicht wie die Pfadkoeffizienten selber approximativ normalverteilt ist.
model_mediation <- "
# Messmodell
UNT_Eltern =~ unt_eltern1 + unt_eltern2
UNT_Freunde =~ unt_freunde1 + unt_freunde2
SWK_Akademisch =~ swk_akad1 + swk_akad2 + swk_akad3 + swk_akad4 + swk_akad5
SWK_Sozial =~ swk_soz1 + swk_soz2 + swk_soz3 + swk_soz4
ZUFRIEDEN =~ leben1 + leben2 + leben3
# Strukturmodell
# regressions
SWK_Akademisch ~ b1 * UNT_Eltern + b3 * UNT_Freunde
SWK_Sozial ~ b2 * UNT_Eltern + b4 * UNT_Freunde
ZUFRIEDEN ~ b5 * UNT_Eltern + b6 * UNT_Freunde + b7 * SWK_Akademisch + b8 * SWK_Sozial
# residual covariances
SWK_Akademisch ~~ SWK_Sozial
# indirect effects
b1b7 := b1 * b7
b2b8 := b2 * b8
totalind_eltern := b1b7 + b2b8
b3b7 := b3 * b7
b4b8 := b4 * b8
totalind_freunde := b3b7 + b4b8
# total effects
total_eltern := totalind_eltern + b5
total_freunde := totalind_freunde + b6
"# Jetzt mit Bootstrap:
# Der iseed-Befehl ist nur für die Replizierbarkeit (vergleichbar mit set.seed())
fit_mediation <- sem(model_mediation,
data = data,
se = "bootstrap",
iseed = 123
)
summary(fit_mediation,
fit.measures = TRUE,
standardized = TRUE
)lavaan 0.6-21 ended normally after 53 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 42
Used Total
Number of observations 262 265
Model Test User Model:
Test statistic 288.018
Degrees of freedom 94
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 2247.066
Degrees of freedom 120
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.909
Tucker-Lewis Index (TLI) 0.884
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -4040.188
Loglikelihood unrestricted model (H1) -3896.179
Akaike (AIC) 8164.376
Bayesian (BIC) 8314.247
Sample-size adjusted Bayesian (SABIC) 8181.088
Root Mean Square Error of Approximation:
RMSEA 0.089
90 Percent confidence interval - lower 0.077
90 Percent confidence interval - upper 0.101
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.895
Standardized Root Mean Square Residual:
SRMR 0.061
Parameter Estimates:
Standard errors Bootstrap
Number of requested bootstrap draws 1000
Number of successful bootstrap draws 1000
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
UNT_Eltern =~
unt_eltern1 1.000 0.773 0.902
unt_eltern2 1.052 0.103 10.234 0.000 0.813 0.830
UNT_Freunde =~
unt_freunde1 1.000 0.756 0.759
unt_freunde2 1.081 0.193 5.595 0.000 0.817 1.004
SWK_Akademisch =~
swk_akad1 1.000 0.687 0.774
swk_akad2 0.779 0.068 11.403 0.000 0.535 0.689
swk_akad3 0.940 0.064 14.618 0.000 0.646 0.797
swk_akad4 0.871 0.066 13.169 0.000 0.599 0.740
swk_akad5 0.888 0.070 12.749 0.000 0.610 0.752
SWK_Sozial =~
swk_soz1 1.000 0.543 0.786
swk_soz2 1.146 0.086 13.360 0.000 0.623 0.794
swk_soz3 0.884 0.076 11.574 0.000 0.480 0.760
swk_soz4 1.094 0.106 10.319 0.000 0.594 0.722
ZUFRIEDEN =~
leben1 1.000 0.396 0.464
leben2 1.233 0.262 4.709 0.000 0.488 0.788
leben3 1.500 0.351 4.274 0.000 0.594 0.766
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
SWK_Akademisch ~
UNT_Eltrn (b1) 0.379 0.073 5.208 0.000 0.427 0.427
UNT_Frend (b3) 0.022 0.067 0.335 0.738 0.025 0.025
SWK_Sozial ~
UNT_Eltrn (b2) 0.270 0.054 4.979 0.000 0.384 0.384
UNT_Frend (b4) 0.224 0.046 4.823 0.000 0.311 0.311
ZUFRIEDEN ~
UNT_Eltrn (b5) 0.226 0.056 4.051 0.000 0.441 0.441
UNT_Frend (b6) 0.043 0.037 1.163 0.245 0.083 0.083
SWK_Akdms (b7) 0.085 0.055 1.530 0.126 0.147 0.147
SWK_Sozil (b8) 0.265 0.107 2.464 0.014 0.363 0.363
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.SWK_Akademisch ~~
.SWK_Sozial 0.170 0.028 6.015 0.000 0.598 0.598
UNT_Eltern ~~
UNT_Freunde 0.098 0.039 2.505 0.012 0.167 0.167
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.unt_eltern1 0.136 0.052 2.610 0.009 0.136 0.186
.unt_eltern2 0.300 0.062 4.844 0.000 0.300 0.312
.unt_freunde1 0.420 0.103 4.069 0.000 0.420 0.424
.unt_freunde2 -0.005 0.110 -0.044 0.965 -0.005 -0.007
.swk_akad1 0.316 0.042 7.484 0.000 0.316 0.401
.swk_akad2 0.317 0.037 8.504 0.000 0.317 0.525
.swk_akad3 0.239 0.028 8.434 0.000 0.239 0.364
.swk_akad4 0.296 0.033 8.918 0.000 0.296 0.452
.swk_akad5 0.286 0.033 8.789 0.000 0.286 0.435
.swk_soz1 0.183 0.030 6.028 0.000 0.183 0.382
.swk_soz2 0.228 0.035 6.539 0.000 0.228 0.370
.swk_soz3 0.168 0.018 9.210 0.000 0.168 0.422
.swk_soz4 0.325 0.039 8.364 0.000 0.325 0.479
.leben1 0.572 0.082 6.989 0.000 0.572 0.785
.leben2 0.146 0.032 4.551 0.000 0.146 0.379
.leben3 0.249 0.044 5.644 0.000 0.249 0.414
UNT_Eltern 0.597 0.080 7.467 0.000 1.000 1.000
UNT_Freunde 0.571 0.118 4.826 0.000 1.000 1.000
.SWK_Akademisch 0.384 0.052 7.437 0.000 0.814 0.814
.SWK_Sozial 0.211 0.029 7.242 0.000 0.715 0.715
.ZUFRIEDEN 0.054 0.019 2.843 0.004 0.343 0.343
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
b1b7 0.032 0.021 1.501 0.133 0.063 0.063
b2b8 0.072 0.032 2.267 0.023 0.140 0.140
totalind_eltrn 0.104 0.029 3.593 0.000 0.202 0.202
b3b7 0.002 0.007 0.285 0.776 0.004 0.004
b4b8 0.059 0.028 2.090 0.037 0.113 0.113
totalind_frend 0.061 0.030 2.052 0.040 0.117 0.117
total_eltern 0.330 0.066 4.964 0.000 0.643 0.643
total_freunde 0.104 0.047 2.240 0.025 0.199 0.199Anmerkung: Auch die Standardfehler der anderen Parameter wurden jetzt per Bootstrap geschätzt. Daher haben sich die p-Werte leicht verändert. An den Signifikanzentscheidungen ändert das aber nichts!
Welche der von Hand berechneten indirekten und totalen Effekte sind nun signifikant?
Spezifische indirekte Effekte
1. UNT_Eltern \(\rightarrow\) SWK_Akademisch \(\rightarrow\) ZUFRIEDEN:
Dieser indirekte Effekt ist nicht signifikant, b1b7 = \(0.063, p = 0.133\).
2. UNT_Eltern \(\rightarrow\) SWK_Sozial \(\rightarrow\) ZUFRIEDEN:
Dieser indirekte Effekt ist signifikant, b2b8 = \(0.14, p = 0.023\).
3. UNT_Freunde \(\rightarrow\) SWK_Akademisch \(\rightarrow\) ZUFRIEDEN:
Dieser indirekte Effekt ist nicht signifikant, b3b7 = \(0.004, p = 0.776\).
4. UNT_Freunde \(\rightarrow\) SWK_Sozial \(\rightarrow\) ZUFRIEDEN:
Dieser indirekte Effekt ist signifikant, b4b8 = \(0.113, p = 0.037\).
\(~\)
Totale indirekte Effekte
1. UNT_Eltern \(\rightarrow\) ZUFRIEDEN über SWK_Akademisch und SWK_Sozial:
Dieser totale indirekte Effekt ist signifikant, totalind_eltern = \(0.202, p < 0.001\).
2. UNT_Freunde \(\rightarrow\) ZUFRIEDEN über SWK_Akademisch und SWK_Sozial:
Dieser totale indirekte Effekt ist signifikant, totalind_freunde = \(0.117, p = 0.04\).
\(~\)
Totale Effekte
1. UNT_Eltern \(\rightarrow\) ZUFRIEDEN:
Dieser totale Effekt ist signifikant, total_eltern = \(0.643, p < 0.001\).
2. UNT_Freunde \(\rightarrow\) ZUFRIEDEN:
Dieser totale Effekt ist signifikant, total_freunde = \(0.199, p = 0.025\).
7.6 Zusammenfassung
Gerade noch akzeptabler Modell-Fit des Messmodells
Strukturmodell saturiert, Modellpassung nicht überprüfbar
Unterstützung durch Eltern am wichtigsten für die Lebenszufriedenheit Jugendlicher
- Totaler Effekt mehr als doppelt so gross im Vergleich zu Unterstützung durch Freunde
- Direkter Effekt am stärksten, aber auch indirekter Effekt über soziale Selbstwirksamkeit substantiell
Unterstützung durch Freunde hat nur indirekt über die soziale Selbstwirksamkeit einen Effekt auf die Lebenszufriedenheit
Akademische Selbstwirksamkeit unter Konstanthaltung der sozialen Selbstwirksamkeit irrelevant für Lebenszufriedenheit
Zusammenfassung der Effekte im Strukturmodell: