# Daten einlesen
library(tidyverse)
lifesat <- read_csv("https://github.com/methodenlehre/data/blob/master/statistik_IV/lifesat.csv?raw=true")Exploratorische Datenreduktion
Das Ziel der Exploratorischen Faktorenanalyse (EFA) und der Hauptkomponentenanalyse (PCA) ist es, Daten zu reduzieren, d.h. die Interkorrelationen von Variablen durch wenige, möglichst voneinander unabhängige “Faktoren” bzw. “Komponenten” zu repräsentieren. Das ist besonders nützlich, wenn wir Daten mit vielen Variablen haben. Beide Verfahren können aufzeigen, welcher Anteil der Gesamtvarianz der Daten erklärt werden kann, wenn die Daten auf eine gewisse Anzahl Komponenten/Faktoren reduziert werden. Typischerweise können so Gruppen von Variablen, die stark miteinander interkorrelieren, zu zugrundeliegenden Dimensionen zusammengefasst werden. Für die Unterschiede zwischen den beiden Verfahren siehe die Vorlesungsunterlagen.
EFA und PCA sind beides explorative Verfahren. Bei beiden wird in der Regel keine a-priori Annahme getroffen, wie viele Dimensionen den Daten zu Grunde liegen.
Die Aufgabe solcher Verfahren ist es zunächst, herauszufinden, wieviele Faktoren extrahiert werden sollten. Wenn auf zu wenige Faktoren reduziert wird, gehen möglicherweise wertvolle Informationen verloren. Extrahiert man zu viele Faktoren, läuft man Gefahr, die Daten zu overfitten und zufällig entstandene Kovarianzen auf einen nicht vorhandenen oder unwichtigen Faktor zurückzuführen.
Die State-of-the-Art Methode, um die Anzahl zu extrahierender Faktoren zu ermitteln, ist die Parallelanalyse. Dabei wird ein Datensatz simuliert, der dieselbe Anzahl Variablen und dieselbe Stichprobengrösse wie der zu analysierende Datensatz aufweist. Die Simulation zieht dabei eine Stichprobe aus einer (imaginären) Population, in der die Interkorrelationen aller Variablen untereinander gleich null sind. Wegen der Zufälligkeit der Stichprobenziehung weisen die Variablen des simulierten Datensatzes aber (geringfügig) von null verschiedene Korrelationen auf. Auf diese Daten wird dann eine EFA oder PCA angewendet und geschaut, welche Eigenwerte die zufälligen Faktoren aufweisen. Wenn die Eigenwerte der extrahierten Faktoren in unserem Datensatz grösser sind als die der entsprechenden zufälligen Faktoren, sollten sie extrahiert werden, da sie dann Varianz repräsentieren, die über das Zufallsniveau hinaus geht. Das macht man nicht nur einmal, sondern normalerweise mindestens 1000 Mal und man betrachtet dann den Mittelwert oder den Median der Verteilung der entsprechenden Eigenwerte. Manchmal - wie per default in der Funktion psych::fa.parallel(), die wir im Folgenden verwenden werden - wird auch das 95 %-Quantil benutzt, dann im Sinne eines Signifikanztests für die “Überzufälligkeit” eines beobachteten Eigenwerts.
Neben der Paralellanalyse, die wichtige empirische Hinweise zur Anzahl der zu extrahierenden Faktoren gibt, gibt es weitere Kriterien wie eine weitergehende Interpretation des empirischen Verlaufs der Eigenwerte (“Scree-Plot”) und die inhaltliche Interpretierbarkeit der Lösung (nach einer Rotation).
Sobald die Anzahl der zu extrahierenden Faktoren festgelegt ist, können die Faktoren so rotiert werden, dass möglichst eine Einfachstruktur erzielt wird. Dies ist dann erreicht, wenn es keine substantiellen Querladungen mehr gibt, jedes Item soll also nur auf einen Faktor laden und die Ladungen der Items auf einem Faktor sollten möglichst hoch und homogen sein.
Daten
Als Beispieldaten benutzen wir Aussagen zur Lebenszufriedenheit von \(n=255\) Jugendlichen zwischen 13 und 17 Jahren, die in einer Fragebogenstudie zur Entwicklung Jugendlicher erhoben wurden.
Die Lebenszufriedenheits-Daten bestehen aus 10 Items, die sich auf verschiedene Aspekte/Bereiche der Lebenszufriedenheit beziehen. Die Jugendlichen wurden gefragt:
“Wie zufrieden bist Du…
| Fragen | |
|---|---|
| leben1 | mit deinen Schulnoten? |
| leben2 | mit deinem Aussehen und deiner Erscheinung? |
| leben3 | mit der Beziehung zu deinen Lehrern? |
| leben4 | mit allem, was mit der Schule zu tun hat? |
| leben5 | mit allem, was mit deiner Beziehung zu anderen Menschen zu tun hat? |
| leben6 | mit deiner Person? |
| leben7 | mit der Beziehung zu deinen Freunden? |
| leben8 | mit der Beziehung zu deinen Eltern? |
| leben9 | mit dem Zusammenleben mit den anderen Familienmitgliedern? |
| leben10 | mit dem Lebensstandard und dem Ansehen deiner Familie? |
Geantwortet wurde auf einer 7-stufigen Skala von 1 = “überhaupt nicht zufrieden” bis 7 = “sehr zufrieden”.
Die Fragen zur Lebenszufriedenheit können in vier Aspekte/Bereiche gegliedert werden:
Familie Item: 8, 9, 10
Schule Item: 1, 3, 4
Selbst Item: 2, 6
Freunde Item: 7, 5
Entsprechend ändern wir jetzt die Namen der Variablen, damit die Zuordnung etwas klarer wird. Um die Reihenfolge der Variablen mit ihrer inhaltlichen Ausrichtung in Übereinstimmung zu bringen, ändern wir die Reihenfolge noch mit relocate()`.
lifesat <- lifesat |>
rename(leben8_familie = leben8,
leben9_familie = leben9,
leben10_familie = leben10,
leben1_schule = leben1,
leben3_schule = leben3,
leben4_schule = leben4,
leben2_selbst = leben2,
leben6_selbst = leben6,
leben5_freunde = leben5,
leben7_freunde = leben7) |>
relocate(leben1_schule, leben3_schule, leben4_schule,
leben2_selbst, leben6_selbst,
leben5_freunde, leben7_freunde,
leben8_familie, leben9_familie, leben10_familie)summary(lifesat) leben1_schule leben3_schule leben4_schule leben2_selbst
Min. :1.000 Min. :1.000 Min. :1.000 Min. :2.000
1st Qu.:4.000 1st Qu.:4.000 1st Qu.:4.000 1st Qu.:5.000
Median :5.000 Median :5.000 Median :5.000 Median :6.000
Mean :4.824 Mean :4.851 Mean :4.518 Mean :5.365
3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:5.000 3rd Qu.:6.000
Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
leben6_selbst leben5_freunde leben7_freunde leben8_familie
Min. :3.000 Min. :3.000 Min. :4.000 Min. :2.000
1st Qu.:5.000 1st Qu.:5.000 1st Qu.:6.000 1st Qu.:5.000
Median :6.000 Median :6.000 Median :6.000 Median :6.000
Mean :5.812 Mean :5.671 Mean :6.243 Mean :6.004
3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:7.000 3rd Qu.:7.000
Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
leben9_familie leben10_familie
Min. :2.000 Min. :3.000
1st Qu.:5.000 1st Qu.:5.000
Median :6.000 Median :6.000
Mean :5.796 Mean :5.949
3rd Qu.:6.000 3rd Qu.:7.000
Max. :7.000 Max. :7.000 Packages
Für EFA und PCA verwenden wir hier das Package psych.
Mit der Funktion principal() können wir PCAs berechnen. Wenn wir die Faktoren nicht rotieren, heissen die Hauptkomponenten im Output PC# (principal component #), zum Beispiel PC1. Rotieren wir die Komponenten mit einer orthogonalen Rotationsmethode, werden sie als RC# (rotated component #) beschrieben, zum Beispiel RC1. Rotieren wir sie mit einer schiefwinkligen (obliquen) Rotationsmethode, werden sie als TC# (transformed component #) beschrieben, zum Beispiel TC1.
Für die EFA verwenden wir die Funktion fa(). Für die von uns betrachtete Maximum-Likelihood-EFA benötigen wir zusätzlich noch das Argument fm = "ml".
Im Package psych nehmen die Funktionen für PCA und EFA direkt das Datenframe als Input. Zusätzlich müssen die Anzahl zu extrahierender Komponenten/Faktoren definiert werden, und ob bzw. wie sie rotiert werden sollen.
Für die ML-EFA: Um Konfidenzintervalle (CI) und Standardfehler (SE) zu schätzen, benötigen wir zusätzlich das Package EFAutilities.
Die Funktion fa.parallel() führt eine Parallelanalyse sowohl für die PCA als auch für die EFA durch.
Beurteilung der Angemessenheit einer PCA/EFA für die Daten
Bevor eine PCA/EFA durchgeführt wird, muss zunächst sichergestellt sein, dass sich die Daten aufgrund ihrer Korrelationsstruktur auch für eine Dimensionsreduktion im Sinne der PCA/EFA eignen. Wir betrachten in einem ersten Schritt die Korrelationsmatrix und verschaffen uns so einen Überblick über die Zusammenhänge in den Daten. Danach führen wir den Bartlett’s Test auf Sphärizität durch, gefolgt von der Berechnung des KMO-MSA (Kaiser-Meyer-Olkin Measure of Sampling Adequacy).
Korrelationen
Deskriptiver Überblick über die Interkorrelationsstruktur der Items: pairs.panels() aus psych gibt einen Plot aus, der Informationen zur Korrelationsmatrix visualisiert. An diesem Plot kann man sehen, dass vor allem diejenigen Items, die zum selben Inhaltsbereich gehören, positive Korrelationen untereinander aufweisen. Es zeigen sich aber auch darüber hinaus (eher schwächere) Korrelationen von Items aus unterschiedlichen Inhaltsbereichen.
pairs.panels(lifesat, density = FALSE, jiggle = TRUE, ci = TRUE, stars = TRUE)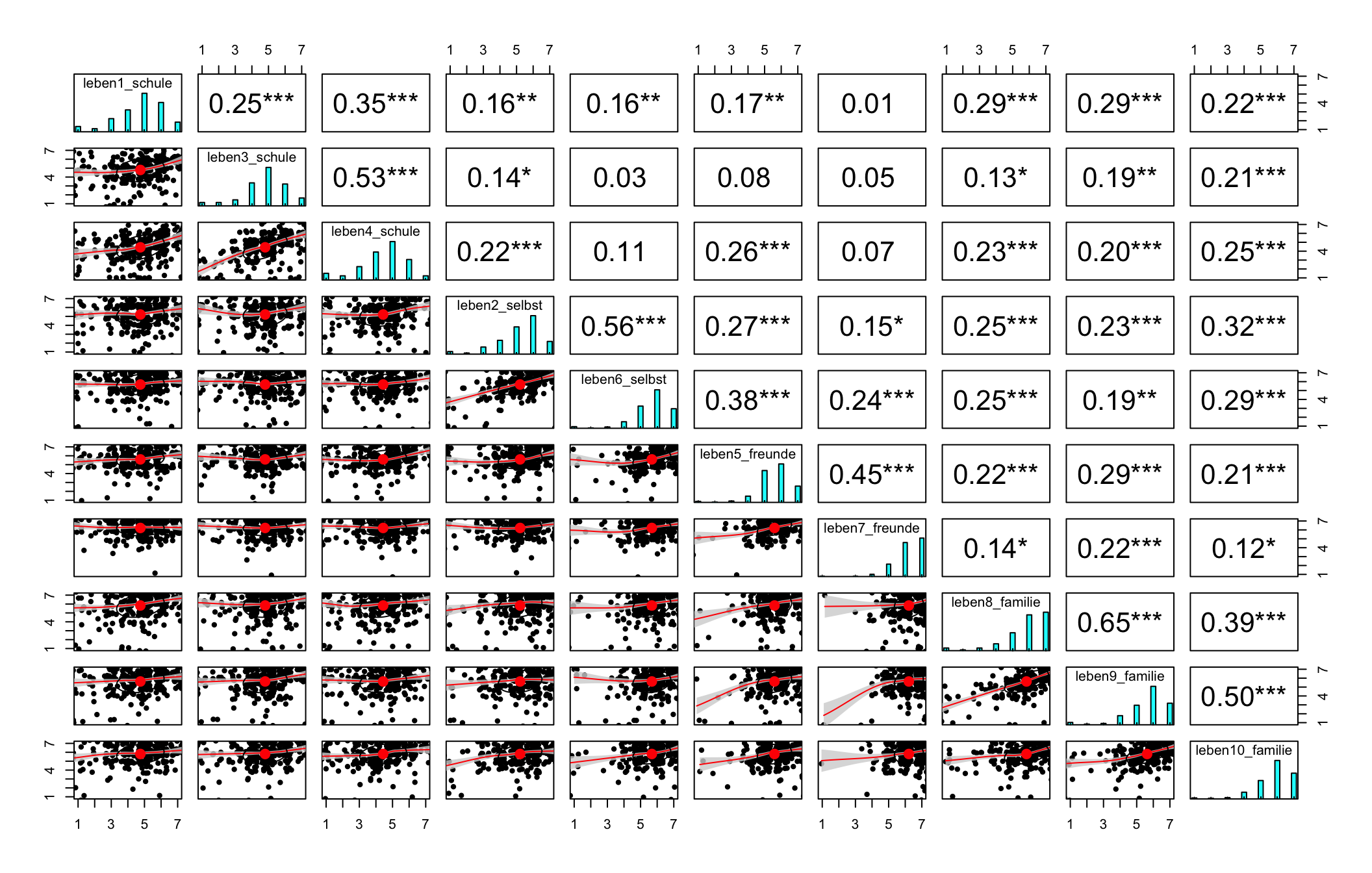
Bartlett’s Test auf Sphärizität
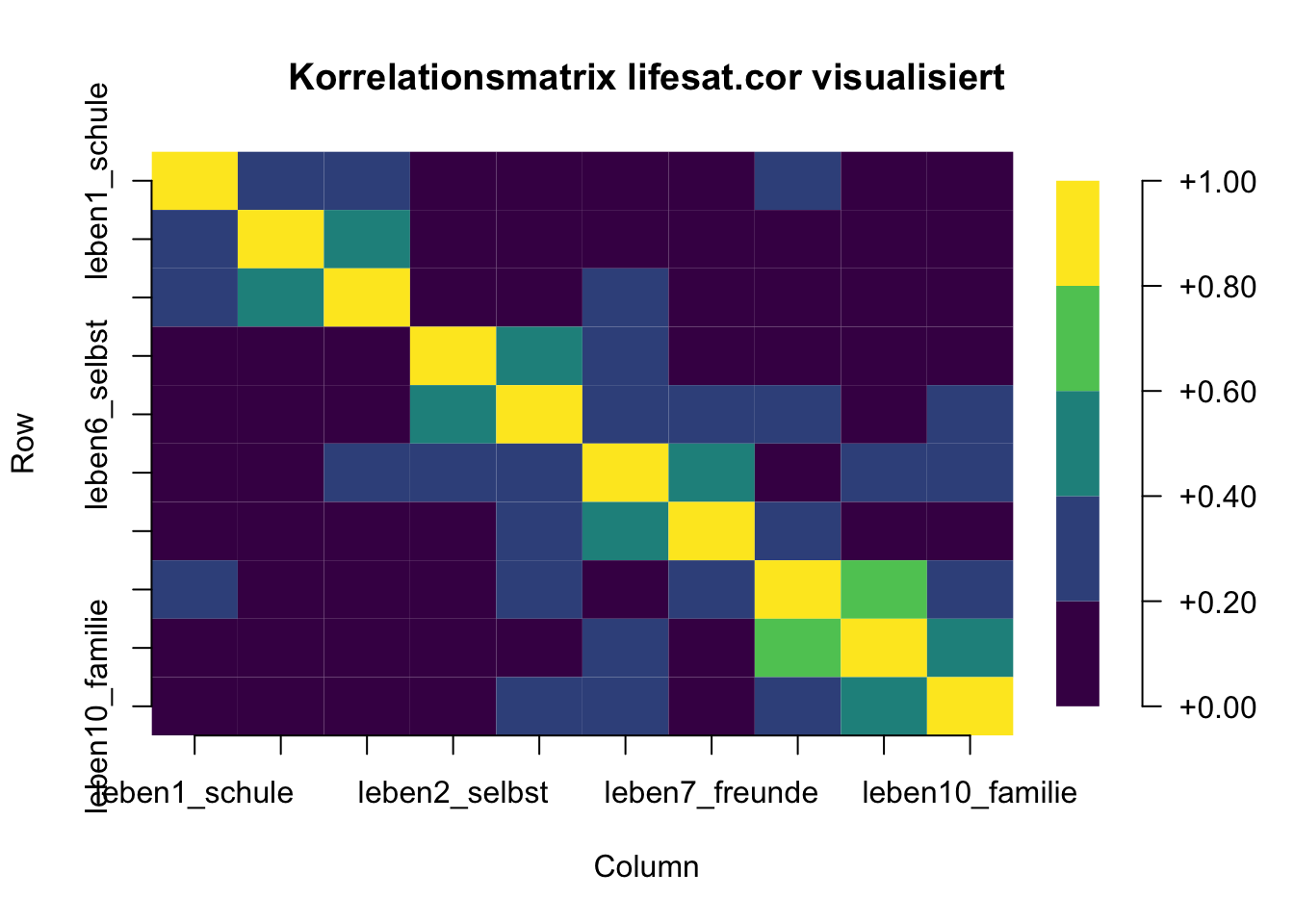
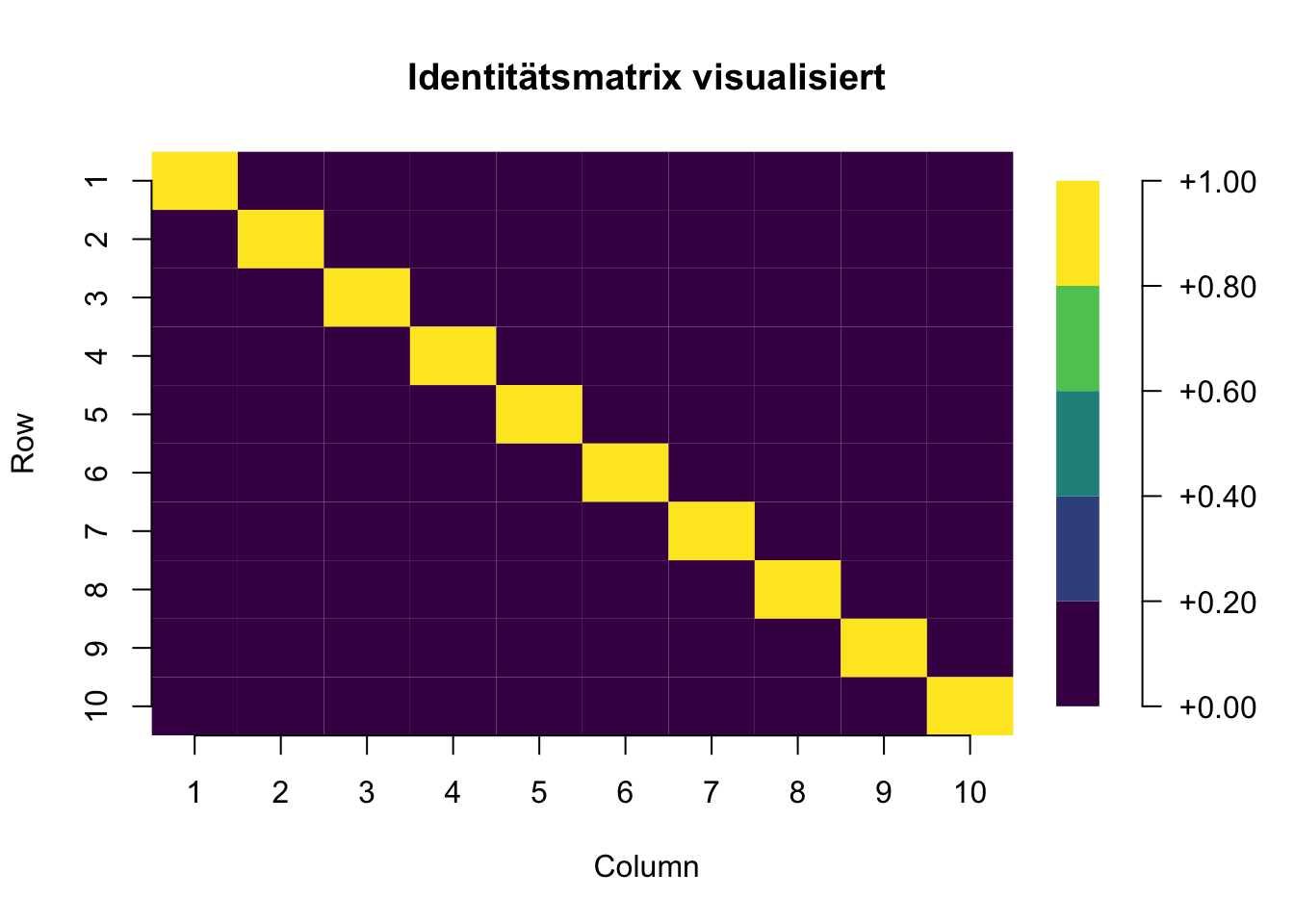
Der Bartlett’s Test auf Sphärizität bewertet, ob die Variablen überhaupt miteinander korrelieren oder nicht, indem er die beobachtete Korrelationsmatrix gegen eine “Identitätsmatrix” (eine Matrix mit Einsen entlang der Hauptdiagonalen und Nullen überall sonst) testet. Wenn dieser Test statistisch nicht signifikant ist, sollten faktoranalytische Verfahren grundsätzlich nicht verwendet werden.
# Zuerst brauchen wir eine Korrelationsmatrix
lifesat.cor <- cor(lifesat)
# Bartlett's Test
cortest.bartlett(lifesat.cor, n = length(lifesat$leben1_schule))$chisq
[1] 571.2263
$p.value
[1] 2.604884e-92
$df
[1] 45Der Bartlett Test ist signifikant. Es gibt also insgesamt signifikante Interkorrelationen der Items, eine Grundvoraussetzung für die Faktorenanalyse.
Visualisiert bedeutet das, dass der Bartlett Test folgende Matrizen verglichen und Unterschiede festgestellt hat.
KMO-MSA (Kaiser-Meyer-Olkin Measure of Sampling Adequacy)
Das KMO-MSA stellt eine Masszahl für die Bewertung der Eignung der beobachteten Variablen für eine Faktorenanalyse dar. Es prüft unter anderem, ob die partiellen Korrelationen der Variablen (bivariate Korrelationen partialisiert für jeweils alle anderen Variablen) nahe genug an Null liegen, um darauf hinzudeuten, dass den Variablen mindestens ein latenter Faktor zugrunde liegt. Ein höheres KMO-MSA weist auf eine bessere Eignung hin. Das KMO-MSA ist ganz einfach mit der KMO-Funktion des psych-Packages zu finden.
# Die KMO-Funktion nimmt als Input entweder das Datenframe oder
# eine Korrelationsmatrix. Einfachheitshalber verwenden wir hier
# das Datenframe als input.
KMO(lifesat)Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = lifesat)
Overall MSA = 0.68
MSA for each item =
leben1_schule leben3_schule leben4_schule leben2_selbst leben6_selbst
0.73 0.60 0.62 0.66 0.68
leben5_freunde leben7_freunde leben8_familie leben9_familie leben10_familie
0.74 0.70 0.67 0.64 0.79 Im Output findet man den Overall MSA: Einen Kennwert der anzeigt, wie gut sich die Daten (d.h. alle Variablen zusammen) insgesamt für eine Faktorenanalyse eignen. Zusätzlich wird für jedes Item ein MSA ausgegeben.
Nach Kaiser (1974) sind Kennwerte unter 0,5 inakzeptabel (unacceptable), ab 0,5 schlecht (miserable), ab 0,6 mässig (mediocre), ab 0,7 mittelmässig (middling), ab 0,8 gut (meritorious) und ab 0,9 hervorragend (marvelous). Bühner (2021) vertritt die Auffassung, dass nur KMO-MSA-Werte von < 0,5 als problematisch zu werten sind.
Unsere Daten eignen sich also mit einem Gesamt-KMO-MSA von 0,68 mässig für eine Hauptkomponentenanalyse/Faktorenanalyse. Für die einzelnen Variablen können wir von einer mässigen bis zu einer mittelmässigen Eignung sprechen (MSAs zwischen 0,60 und 0,79).
Literatur
Bühner, M. (2021). Einführung in die Test- und Fragebogenkonstruktion (4., korrigierte und erweiterte Auflage). Pearson Studium.
Kaiser, H. F. (1974). An index of factorial simplicity. Psychometrika, 39, 31–36. https://doi.org/10.1007/BF02291575