5  Exploratorische Faktorenanalyse (EFA)

5.1 Setup

pacman::p_load(tidyverse, ggplot2, ggthemes, psych, haven, EFAutilities, knitr)

Wir lesen die im einführenden Kapitel zur Exploratorischen Datenreduktion vorgestellten Daten zur Lebenszufriedenheit nochmals ein und führen im selben Schritt die Umbenennung und Umsortierung durch:

lifesat <- read_csv("https://github.com/methodenlehre/data/blob/master/statistik_IV/lifesat.csv?raw=true") |> 
  rename(leben8_familie = leben8,
         leben9_familie = leben9,
         leben10_familie = leben10,
         leben1_schule = leben1,
         leben3_schule = leben3,
         leben4_schule = leben4,
         leben2_selbst = leben2,
         leben6_selbst = leben6,
         leben5_freunde = leben5,
         leben7_freunde = leben7) |> 
  relocate(leben1_schule, leben3_schule, leben4_schule, 
           leben2_selbst, leben6_selbst, 
           leben5_freunde, leben7_freunde, 
           leben8_familie, leben9_familie, leben10_familie)

5.2 Parallelanalyse

Zuerst führen wir eine Parallelanalyse durch. Weil wir die Parallelanalyse jetzt für die Faktorenanalyse berechnen (und nicht wie im vorigen Kapitel für die Hauptkomponentenanalyse), spezifizieren wir jetzt fa = "fa". Ausserdem benutzen wir das Argument fm = "ml", damit die Parallelanalyse auf einer Maximum-Likelihood-Faktorenanalyse basiert.

parallelAnalyse <- fa.parallel(lifesat,
  n.iter = 1000, fa = "fa",
  fm = "ml", quant = 0.5
)

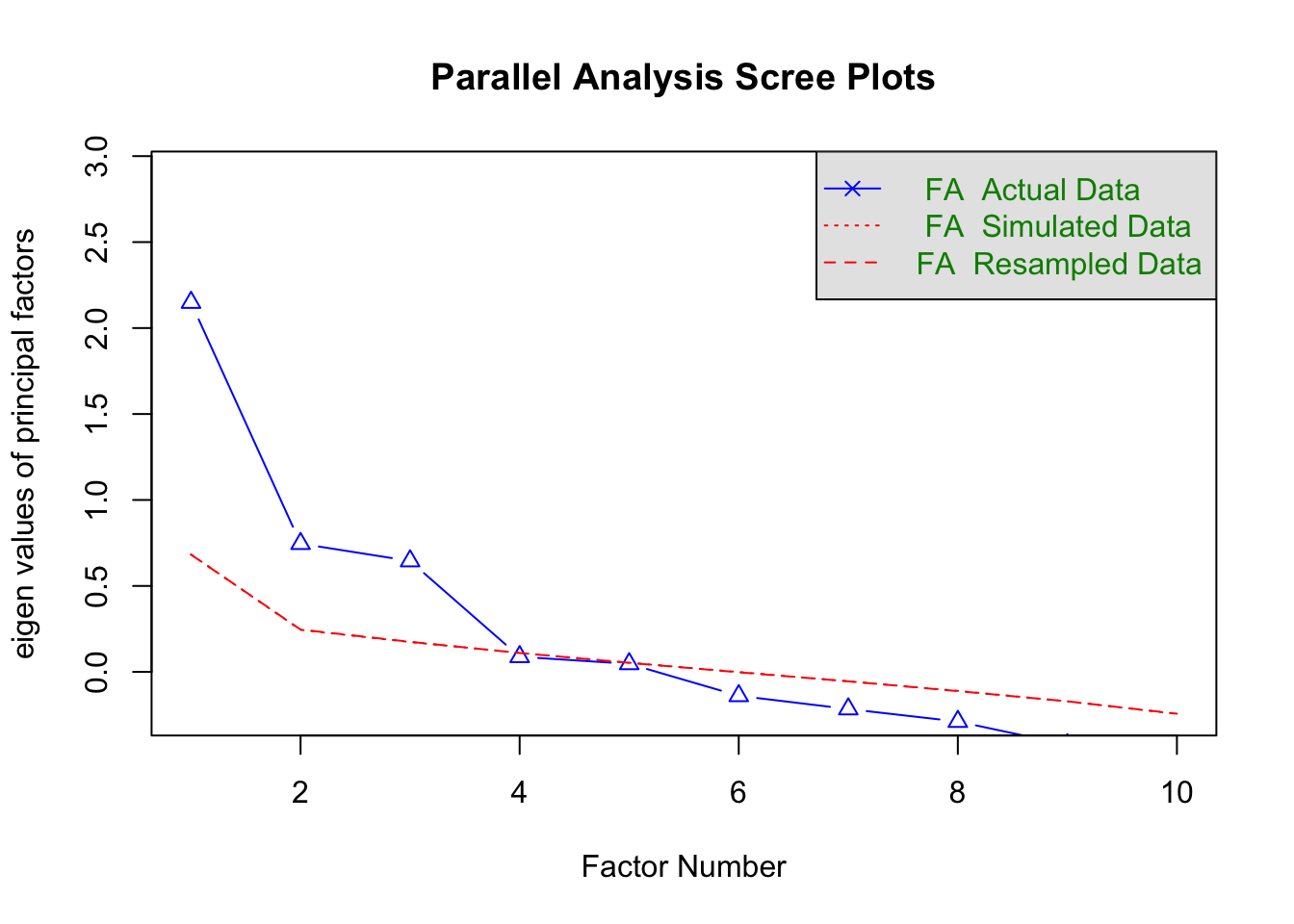
Parallel analysis suggests that the number of factors =  3  and the number of components =  NA 

Die Parallelanalyse zur ML-EFA zeigt, dass auch hier drei Faktoren extrahiert werden sollten. Der Eigenwert des vierten Faktors liegt knapp unter dem Median der 1000 simulierten vierten Eigenwerte einer Zufallsmatrix.

5.3 ML-EFA mit drei unrotierten Faktoren

# Unrotierte EFA mit 3 Faktoren
efa.3.unrotiert <- fa(lifesat, fm = "ml", nfactors = 3, rotate = "none")
print.psych(efa.3.unrotiert, sort = TRUE)

Factor Analysis using method =  ml
Call: fa(r = lifesat, nfactors = 3, rotate = "none", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                item  ML1   ML2   ML3   h2   u2 com
leben4_schule      3 0.83 -0.42 -0.07 0.87 0.13 1.5
leben3_schule      2 0.55 -0.22 -0.11 0.36 0.64 1.4
leben1_schule      1 0.43  0.00 -0.01 0.18 0.82 1.0
leben10_familie   10 0.41  0.33  0.06 0.28 0.72 2.0
leben9_familie     9 0.48  0.73 -0.20 0.81 0.19 1.9
leben8_familie     8 0.43  0.57 -0.04 0.51 0.49 1.9
leben6_selbst      5 0.27  0.20  0.70 0.60 0.40 1.5
leben2_selbst      4 0.27  0.06  0.59 0.43 0.57 1.4
leben5_freunde     6 0.37  0.14  0.40 0.32 0.68 2.2
leben7_freunde     7 0.23  0.16  0.30 0.17 0.83 2.5

                       ML1  ML2  ML3
SS loadings           2.09 1.29 1.15
Proportion Var        0.21 0.13 0.12
Cumulative Var        0.21 0.34 0.45
Proportion Explained  0.46 0.28 0.25
Cumulative Proportion 0.46 0.75 1.00

Mean item complexity =  1.7
Test of the hypothesis that 3 factors are sufficient.

df null model =  45  with the objective function =  2.29 with Chi Square =  571.23
df of  the model are 18  and the objective function was  0.16 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.06 

The harmonic n.obs is  255 with the empirical chi square  36.34  with prob <  0.0064 
The total n.obs was  255  with Likelihood Chi Square =  39.98  with prob <  0.0021 

Tucker Lewis Index of factoring reliability =  0.895
RMSEA index =  0.069  and the 90 % confidence intervals are  0.04 0.098
BIC =  -59.76
Fit based upon off diagonal values = 0.97
Measures of factor score adequacy             
                                                   ML1  ML2  ML3
Correlation of (regression) scores with factors   0.95 0.92 0.84
Multiple R square of scores with factors          0.89 0.84 0.71
Minimum correlation of possible factor scores     0.79 0.68 0.42

Insgesamt können mit drei Faktoren 45 % der Gesamtvarianz erklärt werden. Die Eigenwerte entsprechen (anders als bei der PCA) hier übrigens nicht denen der Parallelanalyse. Das hängt damit zusammen, dass die Eigenwerte in der EFA auch von der Anzahl der extrahierten Faktoren abhängen, in der PCA dagegen nicht.

Der Anpassungstest für das Modell (“Test of the hypothesis that 3 factors are sufficient.”) zeigt ein \(\chi^2 = 39.98, p = 0.002\). Somit muss die Nullhypothese, dass drei Faktoren ausreichen, um die Korrelationen zwischen den Items vollständig zu erklären, abgelehnt werden. Auch die weiteren Fit-Indizes, die wir erst bei der CFA genauer kennenlernen werden, zeigen keinen besonders guten Fit an. Aus diesem Grund werden wir weiter unten auch noch eine 4-Faktor-Lösung betrachten.

5.4 ML-EFA mit drei rotierten Faktoren

Zunächst betrachten wir aber eine rotierte Lösung für drei Faktoren. Eine orthogonale Rotation lassen wir diesmal aus und betrachten gleich eine schiefwinklige Rotation. Anders als oben bei der PCA benutzen wir hier keine Oblimin-Rotation, sondern eine oblique Geomin-Rotation. Der Grund ist, dass die Oblimin-Rotation im Package EFAutilities, das uns weiter unten die ML-geschätzten Standardfehler und Konfidenzintervalle der Ladungen und Faktorkorrelationen liefern soll, nicht enthalten ist. Die oblique Geomin-Rotation liefert aber sehr ähnliche Ergebnisse wie eine Oblimin-Rotation.

# Rotierte EFA mit 3 Faktoren
efa.3.rotiert <- fa(lifesat, fm = "ml", nfactors = 3, rotate = "geominQ")
print.psych(efa.3.rotiert, sort = TRUE)

Factor Analysis using method =  ml
Call: fa(r = lifesat, nfactors = 3, rotate = "geominQ", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                item   ML2   ML3   ML1   h2   u2 com
leben9_familie     9  0.92 -0.06 -0.02 0.81 0.19 1.0
leben8_familie     8  0.69  0.08  0.00 0.51 0.49 1.0
leben10_familie   10  0.43  0.16  0.10 0.28 0.72 1.4
leben6_selbst      5  0.01  0.79 -0.09 0.60 0.40 1.0
leben2_selbst      4 -0.08  0.67  0.03 0.43 0.57 1.0
leben5_freunde     6  0.10  0.49  0.10 0.32 0.68 1.2
leben7_freunde     7  0.11  0.36  0.01 0.17 0.83 1.2
leben4_schule      3 -0.04  0.01  0.94 0.87 0.13 1.0
leben3_schule      2  0.05 -0.05  0.60 0.36 0.64 1.0
leben1_schule      1  0.16  0.06  0.34 0.18 0.82 1.5

                       ML2  ML3  ML1
SS loadings           1.61 1.52 1.40
Proportion Var        0.16 0.15 0.14
Cumulative Var        0.16 0.31 0.45
Proportion Explained  0.36 0.33 0.31
Cumulative Proportion 0.36 0.69 1.00

 With factor correlations of 
     ML2  ML3  ML1
ML2 1.00 0.28 0.19
ML3 0.28 1.00 0.23
ML1 0.19 0.23 1.00

Mean item complexity =  1.1
Test of the hypothesis that 3 factors are sufficient.

df null model =  45  with the objective function =  2.29 with Chi Square =  571.23
df of  the model are 18  and the objective function was  0.16 

The root mean square of the residuals (RMSR) is  0.04 
The df corrected root mean square of the residuals is  0.06 

The harmonic n.obs is  255 with the empirical chi square  36.34  with prob <  0.0064 
The total n.obs was  255  with Likelihood Chi Square =  39.98  with prob <  0.0021 

Tucker Lewis Index of factoring reliability =  0.895
RMSEA index =  0.069  and the 90 % confidence intervals are  0.04 0.098
BIC =  -59.76
Fit based upon off diagonal values = 0.97
Measures of factor score adequacy             
                                                   ML2  ML3  ML1
Correlation of (regression) scores with factors   0.92 0.87 0.94
Multiple R square of scores with factors          0.86 0.75 0.88
Minimum correlation of possible factor scores     0.71 0.50 0.77

Wie bei der PCA ergeben sich hier ein Familien-Faktor (ML2), eine Selbst- und Freunde-Faktor (ML3) und ein Schul-Faktor (ML1). Die Faktorkorrelationen sind ähnlich wie bei der PCA relativ gleichmässig: \((r_{ML_1ML_2} = 0.19, r_{ML_1ML_3} = 0.23, r_{ML_2ML_3} = 0.28)\).

5.4.1 Konfidenzintervalle und Standardfehler

Mit der Funktion fa() aus psych ist es nicht möglich, Standardfehler und Konfidenzintervalle für die Ladungen einer Maximum-Likelihood-EFA zu berechnen. Mit der Funktion efa() aus dem Package EFAutilities ist dies dagegen möglich. Wie oben werden mit der ML-Methode (fm = "ml") 3 Faktoren (factors = 3) extrahiert und dann eine oblique Geomin-Rotation durchgeführt (rtype = "oblique", rotation = "geomin"). Ausserdem werden mit LConfid = c(.95, .90) zwei Konfidenzkoeffizienten spezifiziert: der erste (0.95) bezieht sich auf die Konfidenzintervalle der Faktorladungen und -korrelationen, der zweite (0.90) ausschliesslich auf den Fit-Index RMSEA, den wir erst beim Thema CFA genauer betrachten. Alle uns hier interessierenden Konfidenzintervalle sind also 95 %-Konfidenzintervalle.

Da der Output von EFAutilities::efa() unübersichtlich ist und wir uns hier nur für das Feature “Standardfehler und CIs” der Ladungen interessieren, haben wir den Output so formatiert, dass eine Tabelle mit den Ladungen zusammen mit ihren Standardfehlern (SEs) sowie eine weitere mit den Ladungen zusammen mit ihren Konfidenzintervallen (CIs) ausgegeben wird:

efa.ci.rotated <- EFAutilities::efa(lifesat,
  fm = "ml", factors = 3,
  rtype = "oblique",
  rotation = "geomin",
  LConfid = c(.95, .90)
)

Ladungen mit Standardfehlern

	F1	F2	F3
leben1_schule	0.34 [se=0.07]	0.16 [se=0.08]	0.06 [se=0.07]
leben3_schule	0.6 [se=0.09]	0.05 [se=0.06]	-0.05 [se=0.06]
leben4_schule	0.94 [se=0.11]	-0.04 [se=0.02]	0.01 [se=0.02]
leben2_selbst	0.03 [se=0.04]	-0.08 [se=0.06]	0.67 [se=0.06]
leben6_selbst	-0.09 [se=0.05]	0.01 [se=0.02]	0.79 [se=0.06]
leben5_freunde	0.1 [se=0.06]	0.1 [se=0.07]	0.49 [se=0.08]
leben7_freunde	0.01 [se=0.06]	0.11 [se=0.08]	0.36 [se=0.09]
leben8_familie	0 [se=0.04]	0.69 [se=0.07]	0.08 [se=0.06]
leben9_familie	-0.02 [se=0.03]	0.92 [se=0.07]	-0.06 [se=0.03]
leben10_familie	0.1 [se=0.06]	0.43 [se=0.06]	0.16 [se=0.07]

Ladungen mit Konfidenzintervallen

	F1	F2	F3
leben1_schule	0.34 [0.197; 0.484]	0.16 [0.01; 0.319]	0.06 [-0.087; 0.199]
leben3_schule	0.6 [0.418; 0.777]	0.05 [-0.056; 0.162]	-0.05 [-0.167; 0.063]
leben4_schule	0.94 [0.725; 1.148]	-0.04 [-0.081; 0.007]	0.01 [-0.035; 0.059]
leben2_selbst	0.03 [-0.039; 0.099]	-0.08 [-0.195; 0.027]	0.67 [0.552; 0.785]
leben6_selbst	-0.09 [-0.195; 0.013]	0.01 [-0.032; 0.043]	0.79 [0.666; 0.914]
leben5_freunde	0.1 [-0.018; 0.226]	0.1 [-0.039; 0.237]	0.49 [0.331; 0.652]
leben7_freunde	0.01 [-0.12; 0.133]	0.11 [-0.043; 0.263]	0.36 [0.192; 0.532]
leben8_familie	0 [-0.078; 0.069]	0.69 [0.548; 0.833]	0.08 [-0.044; 0.197]
leben9_familie	-0.02 [-0.07; 0.032]	0.92 [0.788; 1.052]	-0.06 [-0.114; -0.01]
leben10_familie	0.1 [-0.019; 0.224]	0.43 [0.307; 0.545]	0.16 [0.013; 0.303]

In beiden Tabelle ist jetzt F1 der Schul-Faktor, F2 der Familien-Faktor, und F3 der Selbst- und Freunde-Faktor. Die Konfidenzintervalle aller Ladungen von Items auf einem zugehörigen Faktor sollten den Wert 0 nicht beinhalten und damit signifikant sein, während die Konfidenzintervalle aller Ladungen von Items auf einem nicht zugehörigen Faktor den Wert 0 möglichst beinhalten sollten und damit nicht signifikant sein. Das ist auch weitgehend der Fall: Ausnahmen sind nur die Querladungen von leben1_schule auf F2 (Familie), leben10_familie auf F3 (Selbst und Freunde) sowie die sehr kleine (und negative) Querladung von leben9_familie auf F3 (Selbst und Freunde). Die CIs dieser Ladungen beinhalten den Wert 0 nicht, sind daher also als signifikant zu werten.

Die folgende Tabelle stellt die Faktorkorrelationen mit den zugehörigen Konfidenzintervallen dar. Alle Faktorkorrelationen sind signifikant, da das CI den Wert 0 jeweils nicht enthält.

Anmerkung: Wegen der Darstellung in Matrixform sind 1) alle Korrelationen der Faktoren F1, F2, und F3 untereinander doppelt enthalten; sowie 2) die Korrelationen der Faktoren mit sich selbst enthalten (alle gleich 1, mit CIs [1; 1]).

Faktor-Korrelationen mit Konfidenzintervallen

	F1	F2	F3
F1	1 [1; 1]	0.19 [0.052; 0.329]	0.23 [0.083; 0.375]
F2	0.19 [0.052; 0.329]	1 [1; 1]	0.28 [0.13; 0.412]
F3	0.23 [0.083; 0.375]	0.28 [0.13; 0.412]	1 [1; 1]

Die direkte Ausgabe der Standardfehler sowie der Unter- und Obergrenzen der Konfidenzintervalle der Faktorladungen und -korrelationen erhält man folgendermassen:

efa.ci.rotated$rotatedse # Standardfehler der rotierten Ladungen

             F1         F2         F3
MV1  0.07323054 0.07896098 0.07279374
MV2  0.09158448 0.05557178 0.05878718
MV3  0.10781818 0.02245851 0.02412235
MV4  0.03522391 0.05666046 0.05938844
MV5  0.05311046 0.01920825 0.06309341
MV6  0.06231314 0.07030576 0.08196255
MV7  0.06441949 0.07815184 0.08697391
MV8  0.03744247 0.07262662 0.06157558
MV9  0.02606266 0.06726398 0.02650615
MV10 0.06193819 0.06048478 0.07405738

efa.ci.rotated$rotatedlow # Untere Grenzen CIs der rotierten Ladungen

              F1           F2          F3
MV1   0.19674615  0.009502101 -0.08670332
MV2   0.41830820 -0.056312732 -0.16718555
MV3   0.72500297 -0.081476918 -0.03539280
MV4  -0.03939971 -0.194653180  0.55190964
MV5  -0.19523979 -0.031849079  0.66623238
MV6  -0.01838197 -0.038737566  0.33080616
MV7  -0.11986438 -0.043242494  0.19156306
MV8  -0.07784847  0.548364847 -0.04430198
MV9  -0.06986857  0.788383998 -0.11380585
MV10 -0.01853133  0.307445032  0.01287402

efa.ci.rotated$rotatedupper # Obere Grenzen CIs der rotierten Ladungen

             F1          F2          F3
MV1  0.48380457 0.319023472  0.19864291
MV2  0.77731279 0.161524640  0.06325596
MV3  1.14764247 0.006558823  0.05916508
MV4  0.09867548 0.027451738  0.78470805
MV5  0.01294938 0.043445864  0.91355401
MV6  0.22588106 0.236855938  0.65209346
MV7  0.13265537 0.263107108  0.53249451
MV8  0.06892331 0.833055965  0.19706985
MV9  0.03229517 1.052053961 -0.00990364
MV10 0.22426192 0.544541004  0.30317361

efa.ci.rotated$Philow # Untere Grenzen CIs der Faktorkorrelationen

           F1         F2         F3
F1 1.00000000 0.05173468 0.08306503
F2 0.05173468 1.00000000 0.13040686
F3 0.08306503 0.13040686 1.00000000

efa.ci.rotated$Phiupper # Obere Grenzen CIs der Faktorkorrelationen

         F1        F2        F3
F1 1.000000 0.3293440 0.3748050
F2 0.329344 1.0000000 0.4117514
F3 0.374805 0.4117514 1.0000000

Visualisierung:

Welche Items laden auf welche Faktoren? Hier sieht man auch die Korrelationen zwischen den Faktoren:

fa.diagram(efa.3.rotiert, cut = 0)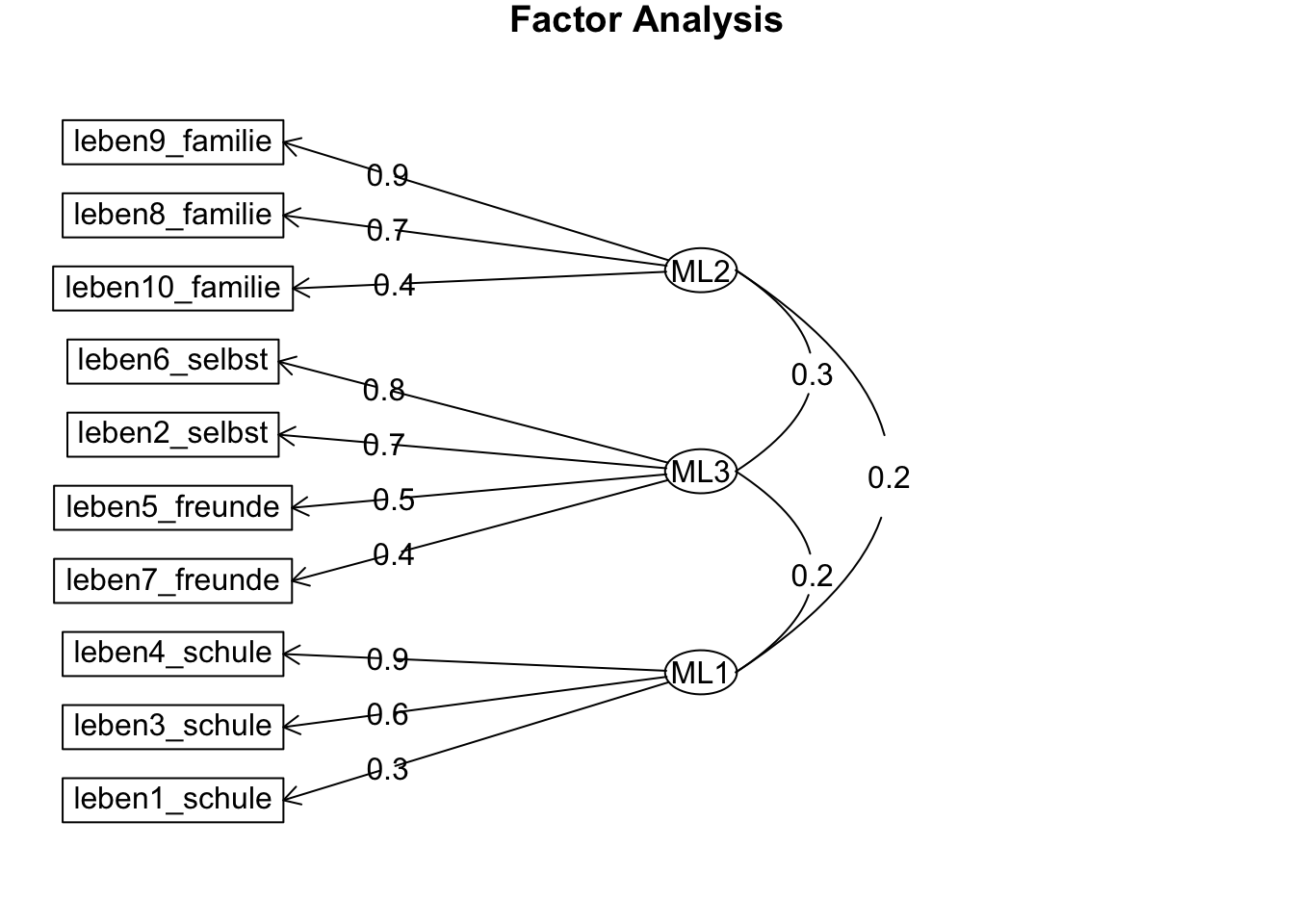

5.5 ML-EFA mit vier unrotierten Faktoren

Unrotierte exploratorische Faktorenanalyse mit 4 Faktoren:

efa.4.unrotiert <- fa(lifesat, fm = "ml", nfactors = 4, rotate = "none")
print.psych(efa.4.unrotiert, sort = TRUE)

Factor Analysis using method =  ml
Call: fa(r = lifesat, nfactors = 4, rotate = "none", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                item  ML1   ML3   ML4   ML2   h2    u2 com
leben5_freunde     6 0.83 -0.01  0.00  0.56 1.00 0.005 1.8
leben6_selbst      5 0.83  0.00  0.00 -0.56 1.00 0.005 1.8
leben2_selbst      4 0.52  0.01  0.11 -0.16 0.31 0.687 1.3
leben7_freunde     7 0.42  0.07 -0.04  0.13 0.20 0.799 1.3
leben9_familie     9 0.21  0.77 -0.42  0.06 0.81 0.188 1.7
leben8_familie     8 0.25  0.60 -0.29 -0.01 0.51 0.492 1.8
leben10_familie   10 0.28  0.44 -0.09 -0.03 0.28 0.723 1.8
leben1_schule      1 0.19  0.33  0.21  0.03 0.19 0.808 2.4
leben4_schule      3 0.19  0.47  0.73  0.12 0.80 0.198 2.0
leben3_schule      2 0.06  0.40  0.48  0.06 0.39 0.605 2.0

                       ML1  ML3  ML4  ML2
SS loadings           2.08 1.64 1.08 0.69
Proportion Var        0.21 0.16 0.11 0.07
Cumulative Var        0.21 0.37 0.48 0.55
Proportion Explained  0.38 0.30 0.20 0.13
Cumulative Proportion 0.38 0.68 0.87 1.00

Mean item complexity =  1.8
Test of the hypothesis that 4 factors are sufficient.

df null model =  45  with the objective function =  2.29 with Chi Square =  571.23
df of  the model are 11  and the objective function was  0.06 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  255 with the empirical chi square  12.53  with prob <  0.33 
The total n.obs was  255  with Likelihood Chi Square =  14.32  with prob <  0.22 

Tucker Lewis Index of factoring reliability =  0.974
RMSEA index =  0.034  and the 90 % confidence intervals are  0 0.079
BIC =  -46.63
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   ML1  ML3  ML4  ML2
Correlation of (regression) scores with factors   1.00 0.92 0.90 1.00
Multiple R square of scores with factors          1.00 0.85 0.81 0.99
Minimum correlation of possible factor scores     0.99 0.70 0.62 0.98

Insgesamt können mit vier Faktoren 55 % der Gesamtvarianz erklärt werden. Der Anpassungstest für das Modell (“Test of the hypothesis that 4 factors are sufficient.”) zeigt ein \(\chi^2 = 14.32, p = 0.22\). Somit kann die Nullhypothese, dass vier Faktoren ausreichen, beibehalten werden. Auch die weiteren Fit-Indizes sind deutlich besser als bei der 3-Faktor-Lösung.

5.5.1 ML-EFA mit vier rotierten Faktoren

Geomin-rotierte exploratorische Faktorenanalyse mit 4 Faktoren:

efa.4.rotiert <- fa(lifesat, fm = "ml", nfactors = 4, rotate = "geominQ")
print.psych(efa.4.rotiert, sort = TRUE)

Factor Analysis using method =  ml
Call: fa(r = lifesat, nfactors = 4, rotate = "geominQ", fm = "ml")
Standardized loadings (pattern matrix) based upon correlation matrix
                item   ML3   ML4   ML1   ML2   h2    u2 com
leben9_familie     9  0.92 -0.02 -0.07  0.00 0.81 0.188 1.0
leben8_familie     8  0.70  0.01  0.05  0.00 0.51 0.492 1.0
leben10_familie   10  0.43  0.12  0.13  0.02 0.28 0.723 1.4
leben4_schule      3 -0.04  0.90  0.00  0.03 0.80 0.198 1.0
leben3_schule      2  0.05  0.63 -0.04 -0.06 0.39 0.605 1.0
leben1_schule      1  0.16  0.35  0.06  0.03 0.19 0.808 1.5
leben6_selbst      5  0.02 -0.03  1.00 -0.02 1.00 0.005 1.0
leben2_selbst      4 -0.04  0.09  0.47  0.15 0.31 0.687 1.3
leben5_freunde     6  0.00  0.00 -0.01  1.00 1.00 0.005 1.0
leben7_freunde     7  0.09 -0.01  0.12  0.35 0.20 0.799 1.4

                       ML3  ML4  ML1  ML2
SS loadings           1.59 1.37 1.32 1.20
Proportion Var        0.16 0.14 0.13 0.12
Cumulative Var        0.16 0.30 0.43 0.55
Proportion Explained  0.29 0.25 0.24 0.22
Cumulative Proportion 0.29 0.54 0.78 1.00

 With factor correlations of 
     ML3  ML4  ML1  ML2
ML3 1.00 0.20 0.21 0.25
ML4 0.20 1.00 0.13 0.23
ML1 0.21 0.13 1.00 0.40
ML2 0.25 0.23 0.40 1.00

Mean item complexity =  1.2
Test of the hypothesis that 4 factors are sufficient.

df null model =  45  with the objective function =  2.29 with Chi Square =  571.23
df of  the model are 11  and the objective function was  0.06 

The root mean square of the residuals (RMSR) is  0.02 
The df corrected root mean square of the residuals is  0.05 

The harmonic n.obs is  255 with the empirical chi square  12.53  with prob <  0.33 
The total n.obs was  255  with Likelihood Chi Square =  14.32  with prob <  0.22 

Tucker Lewis Index of factoring reliability =  0.974
RMSEA index =  0.034  and the 90 % confidence intervals are  0 0.079
BIC =  -46.63
Fit based upon off diagonal values = 0.99
Measures of factor score adequacy             
                                                   ML3  ML4  ML1  ML2
Correlation of (regression) scores with factors   0.92 0.91 1.00 1.00
Multiple R square of scores with factors          0.85 0.83 0.99 1.00
Minimum correlation of possible factor scores     0.71 0.67 0.99 0.99

Die Lösung zeigt eine klare Einfachstruktur. Keine Ladung auf einem nicht-zugehörigen Faktor ist > 0.16. Die Einfachstruktur deckt sich auch mit der inhaltlichen Ausrichtung der Lebenszufriedenheitsbereiche: jetzt haben alle Bereiche (Familie, Schule, Selbst, Freunde) ihren eigenen Faktor.

Die Faktorkorrelationen der vier Faktoren sind jetzt nicht mehr so gleichmässig wie noch bei der 3-Komponenten-Lösung: die grösste Korrelation zeigt sich zwischen dem Selbst- und dem Freunde-Faktor: \(r_{ML_1ML_2} = 0.40\) und die geringste zwischen dem Selbst- und dem Schul-Faktor: \(r_{ML_1ML_4} = 0.13\).

Auf die zusätzliche Berechnung von Standardfehlern und Konfidenzintervallen mit EFAutilities::efa() verzichten wir hier.

Visualisierung:

Faktorladung je Item graphisch dargestellt:

factor.plot(efa.4.rotiert)

\(~\)

Welche Items laden auf welche Faktoren?

fa.diagram(efa.4.rotiert, cut = 0)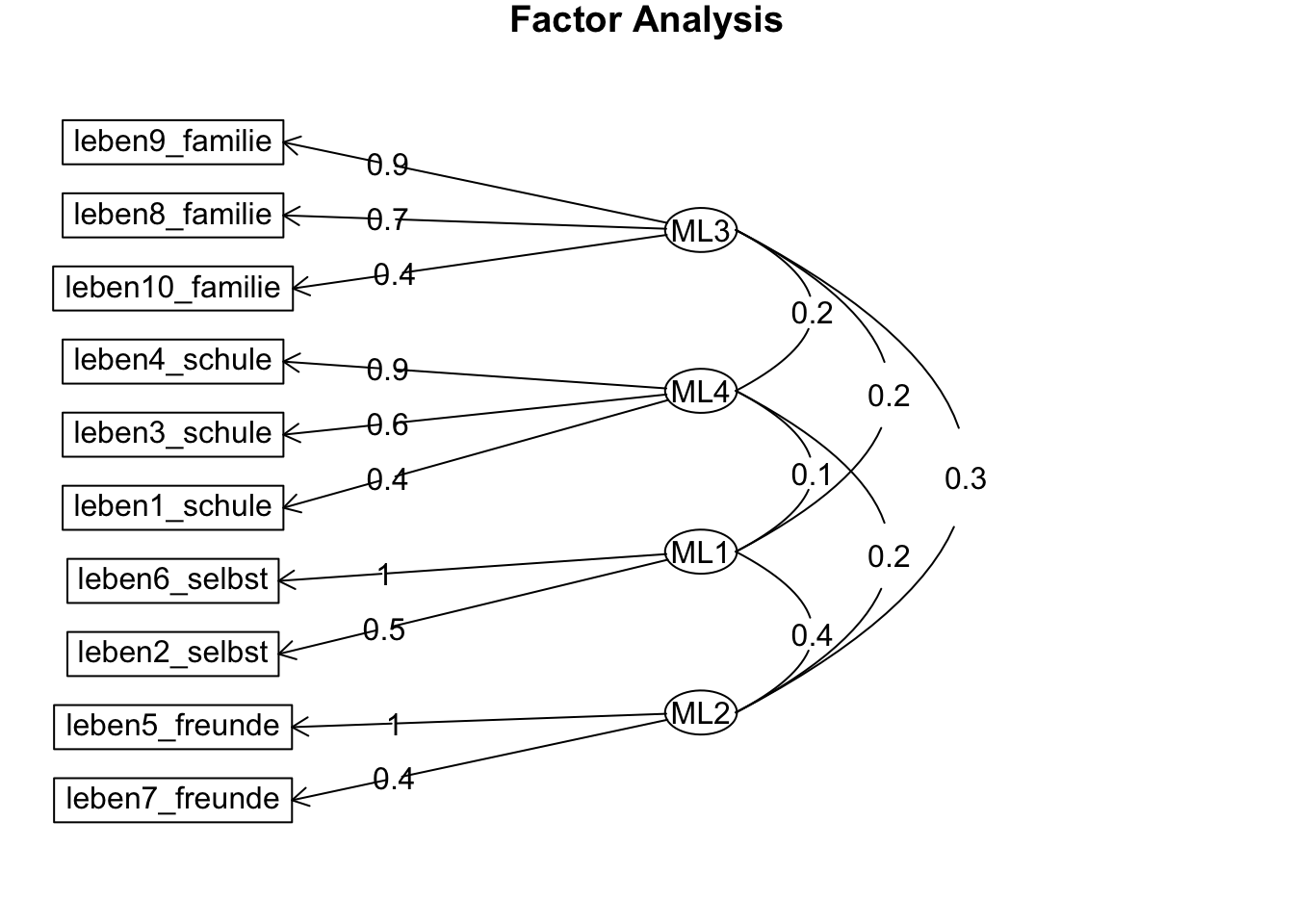

5.6 Zusammenfassung ML-EFA

In der ML-EFA zeigten sich laut Parallelanalyse auch drei Faktoren. Allerdings ist der Chi-Quadrat-Test zur Frage, ob drei Faktoren ausreichen, signifikant. Dies spricht für eine 4-Faktor-Lösung, bei der sich der Selbst-Freunde-Faktor in zwei Faktoren aufspaltet, die die Inhaltsbereiche Selbst und Freunde repräsentieren. Obwohl sich Selbst- und Freunde-Items also viel Varianz teilen und die Parallelanalyse deren Gruppierung auf einem Faktor bevorzugt, müssen diese Inhaltsbereiche im Sinne einer vollständigen Repräsentation der Zusammenhänge separat betrachtet werden.

5.7 Literatur