pacman::p_load(tidyverse, ggplot2, ggthemes, psych, haven, EFAutilities, knitr)4 Hauptkomponentenanalyse (PCA)
4.1 Setup
Wir lesen die im einführenden Kapitel zur Exploratorischen Datenreduktion vorgestellten Daten zur Lebenszufriedenheit nochmals ein und führen im selben Schritt die Umbenennung und Umsortierung durch:
lifesat <- read_csv("https://github.com/methodenlehre/data/blob/master/statistik_IV/lifesat.csv?raw=true") |>
rename(leben8_familie = leben8,
leben9_familie = leben9,
leben10_familie = leben10,
leben1_schule = leben1,
leben3_schule = leben3,
leben4_schule = leben4,
leben2_selbst = leben2,
leben6_selbst = leben6,
leben5_freunde = leben5,
leben7_freunde = leben7) |>
relocate(leben1_schule, leben3_schule, leben4_schule,
leben2_selbst, leben6_selbst,
leben5_freunde, leben7_freunde,
leben8_familie, leben9_familie, leben10_familie)4.2 Parallelanalyse
Zuerst führen wir eine Parallelanalyse durch, um die Anzahl der zu extrahierenden Komponenten zu bestimmen. Weil wir die Parallelanalyse zunächst nur für die PCA berechnen, spezifizieren wir das Argument fa jetzt als "pc" (für principal component). Wenn wir das nicht spezifizieren, wird die Parallelanalyse sowohl für die PCA als auch für die Exploratorische Faktorenanalyse (EFA) zusammen dargestellt werden, was wir hier nicht wollen.
Die Anzahl Iterationen (Zufalls-Samples), die per Default 20 ist, heben wir auf 1000 an, um eine möglichst stabile Lösung zu erhalten.
Als Kriterium für die Anzahl Komponenten wählen wir das Quantil quant = 0.5, also den Median. Das bedeutet, dass die Eigenwerte der tatsächlichen Komponenten, um als substantielle (zu extrahierende) Hauptkomponenten zu gelten, grösser sein müssen als der Eigenwerts-Median der jeweiligen Komponente aus den simulierten Daten (Median von jeweils 1000 simulierten Eigenwerten).
Das unter quant eingestellte Quantil der simulierten Eingenwerteverteilungen bezieht sich allerdings nur auf die im Text ausgegebene Schlussfolgerung, wie viele Komponenten extrahiert werden sollten (im Sinne eines Vergleichs des jeweiligen empirischen Eigenwerts mit diesem Quantil). Die Voreinstellung (default) für diesen Test ist quant = 0.95, ein empirischer Eigenwert wird also nur dann als relevant betrachtet, wenn er den grössten 5 % der simulierten Eigenwerte entspricht.
Die im ausgegeben Plot der Parallelanalyse dargestellte Linie bezieht sich dagegen unabhängig von der quant-Einstellung immer auf den Mittelwert der simulierten Eigenwerteverteilungen. Daher stimmt die ausgegebene Schlussfolgerung nicht in jedem Fall mit der nach dem Plot zu ziehenden Schlussfolgerung überein. Da wir quant = 0.5 verwenden, sollte das für unsere Beispiele aber kaum eine Rolle spielen (da der Median normalerweise sehr nahe am Mittelwert liegt).
parallelAnalyse <- fa.parallel(lifesat, n.iter = 1000, fa = "pc", quant = 0.5)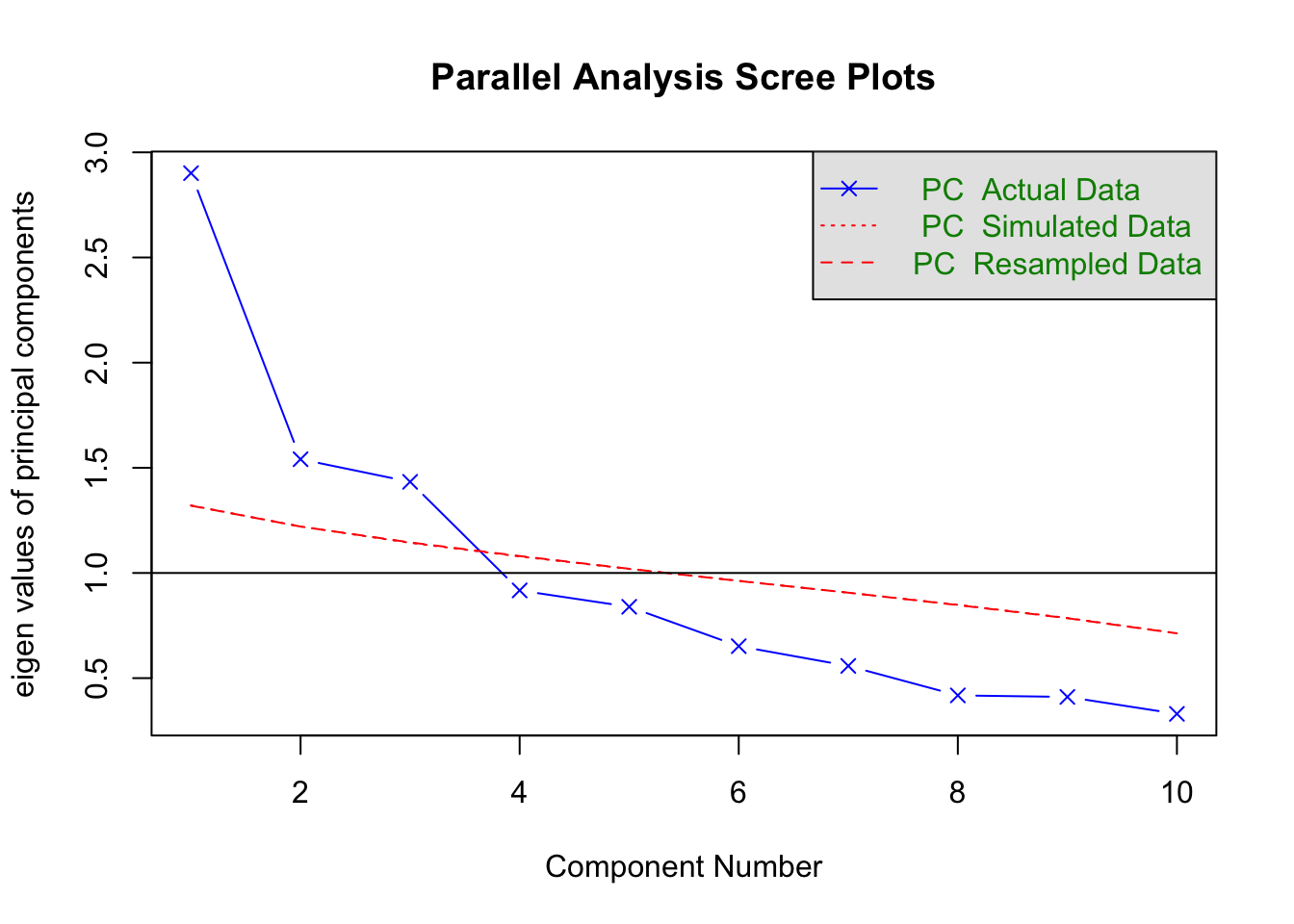
Parallel analysis suggests that the number of factors = NA and the number of components = 3 Die Parallelanalyse der PCA zeigt deutlich drei zu extrahierende Komponenten an, da die vierte Komponente aus random Data einen höheren Eigenwert als die im Datenset gefundene vierte Komponente aufweist. Drei Komponenten würden wir wohl auch nach dem Scree-Kriterium extrahieren, da sich nach der dritten Komponente ein deutlicher “Knick” im Verlauf der Eigenwerte zeigt. Nicht zuletzt sollten auch nach dem Kaiser-Kriterium drei Komponenten extrahiert werden (da der Eigenwert der vierten Komponente bereits < 1 ist).
4.3 Unrotierte Lösung mit drei Hauptkomponenten
Zuerst berechnen wir eine unrotierte PCA:
# Unrotierte PCA
principal(lifesat, nfactors = 3, rotate = "none")Principal Components Analysis
Call: principal(r = lifesat, nfactors = 3, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
PC1 PC2 PC3 h2 u2 com
leben1_schule 0.45 0.42 0.12 0.40 0.60 2.1
leben3_schule 0.41 0.60 0.38 0.68 0.32 2.5
leben4_schule 0.50 0.54 0.45 0.75 0.25 2.9
leben2_selbst 0.50 -0.43 0.39 0.58 0.42 2.9
leben6_selbst 0.57 -0.51 0.20 0.63 0.37 2.2
leben5_freunde 0.62 -0.33 0.22 0.54 0.46 1.8
leben7_freunde 0.48 -0.34 0.09 0.36 0.64 1.9
leben8_familie 0.62 0.08 -0.56 0.71 0.29 2.0
leben9_familie 0.60 0.14 -0.63 0.78 0.22 2.1
leben10_familie 0.58 0.05 -0.33 0.44 0.56 1.6
PC1 PC2 PC3
SS loadings 2.90 1.54 1.43
Proportion Var 0.29 0.15 0.14
Cumulative Var 0.29 0.44 0.59
Proportion Explained 0.49 0.26 0.24
Cumulative Proportion 0.49 0.76 1.00
Mean item complexity = 2.2
Test of the hypothesis that 3 components are sufficient.
The root mean square of the residuals (RMSR) is 0.1
with the empirical chi square 211.22 with prob < 5.6e-35
Fit based upon off diagonal values = 0.85Im Output bekommen wir unter SS loadings (Sum of Squared Loadings) zum einen die Eigenwerte der Komponenten (vgl. Scree-Plot Parallelanalyse). Zum anderen die Anteile bzw. die kumulativen Anteile der durch die Komponenten erklärten Varianz, also den Eigenwert dividiert durch die Anzahl Variablen.
In den letzten beiden Zeilen erhält man noch die Anteile bzw. kumulativen Anteile der erklärten Varianz der jeweiligen Komponenten an der insgesamt durch alle Komponenten erklärten Varianz. Z.B. werden durch die drei Komponenten insgesamt 59 % der Gesamtvarianz erklärt (Cumulative Var \(PC3 = 0.59\)). Also ist die Proportion explained für \(PC1 = 0.29/0.59 = 0.49\) und die für \(PC2 = 0.15/0.59 = 0.25\).
Des weiteren wird noch ein Chi-Quadrat-Test zum Test dafür, dass drei Komponenten ausreichen, ausgegeben. Wir betrachten diesen hier nicht, da dieser Test bei der PCA umstritten ist, weil er trotz der rein datenreduzierenden und damit deskriptiven Funktion der PCA einen Test der verbleibenden Residual(ko-)varianz in der Population durchführt. Mit dieser Art von Test beschäftigen wir uns im folgenden Kapitel zur ML-EFA.
Bei der unrotierten Lösung sieht man relativ grosse Querladungen der einzelnen Items. Das ist normal: Die Komponenten wurden so extrahiert, dass die erste Komponente möglichst viel erklärt, d.h. die Ladungen aller Variablen auf der ersten Komponente wurden maximiert (hier z.B. keine Ladung kleiner als 0.41).
Die variable com im Output steht hier für Komplexität der Items. Je höher die Komplexität, desto mehr laden sie auf verschiedenen Komponenten. Die Berechnung dieser statistischen Grösse behandeln wir hier nicht.
h2 steht für Kommunalität, also den Anteil der Varianz einer beobachteten Variablen, der durch die extrahierten Komponenten erklärt wird. u2 steht für Einzigartigkeit (uniqueness), also für den durch die Komponenten unerklärten Varianzanteil der Variablen (u2 = 1 - h2).
Von Hand berechnet:
Um eine etwas grössere Genauigkeit zu erzielen, sind in folgender Tabelle die Ladungen nochmals auf drei Dezimalstellen gerundet.
| PC1 | PC2 | PC3 | |
|---|---|---|---|
| leben1_schule | 0.453 | 0.422 | 0.115 |
| leben3_schule | 0.408 | 0.605 | 0.383 |
| leben4_schule | 0.500 | 0.545 | 0.451 |
| leben2_selbst | 0.501 | -0.429 | 0.387 |
| leben6_selbst | 0.574 | -0.510 | 0.202 |
| leben5_freunde | 0.616 | -0.334 | 0.218 |
| leben7_freunde | 0.483 | -0.338 | 0.093 |
| leben8_familie | 0.625 | 0.084 | -0.563 |
| leben9_familie | 0.604 | 0.140 | -0.630 |
| leben10_familie | 0.576 | 0.050 | -0.330 |
\(~\) Berechnung des Eigenwerts SS loadings der zweiten Komponente:
\(\begin{aligned} Var(H_2) &= \lambda_{12}^2 + \lambda_{22}^2 + \lambda_{32}^2 + \lambda_{42}^2 + \lambda_{52}^2 + \lambda_{62}^2 + \lambda_{72}^2 + \lambda_{82}^2 + \lambda_{92}^2 + \lambda_{102}^2 \\ &= 0.422^2 + 0.605^2 + 0.545^2 + (-0.429)^2 + (-0.51)^2 + (-0.334)^2 + (-0.338)^2 \\ &{~~~~~}+ 0.084^2 + 0.14^2 + 0.05^2 \\ &= 1.54 \end{aligned}\)
\(~\)
Berechnung der Kommunalität h2 des Items leben2_selbst:
\(\begin{aligned} \hat{H}(Y_4) &= \lambda_{41}^2 + \lambda_{42}^2 + \lambda_{43}^2 \\ &= 0.501^2 + (-0.429)^2 + 0.387^2 \\ &= 0.58 \end{aligned}\)
\(~\)
Berechnung der Uniqueness u2 des Items leben8_familie:
\(\begin{aligned} \hat{U}(Y_8) &= 1 - (\lambda_{81}^2 + \lambda_{82}^2 + \lambda_{83}^2) \\ &= 1 - [0.625^2 + 0.084^2 + (-0.563)^2] \\ &= 0.29 \end{aligned}\)
4.4 Orthogonale Rotation mit drei Hauptkomponenten
Jetzt rotieren wir die Komponenten mit der orthogonalen Varimax-Rotation. Dabei werden die Komponenten so rotiert, dass die Items möglichst wenige Querladungen aufweisen, also bestmöglich eine Einfachstruktur darstellen und gleichzeitig die Orthogonalität der Lösung erhalten bleibt (keine Interkorrelationen der Komponenten).
Im Gegensatz zu obliquen Rotationen bleiben hier die Summen der Eigenwerte identisch. Auch wenn in der aktuellen Literatur meist oblique Rotationsmethoden empfohlen werden, sind orthogonale Rotationen wegen ihrer Eigenschaft, dass die Komponenten weiterhin als unabhängige Dimensionen interpretiert werden können, attraktiv (insbesondere wenn sich damit eine Einfachstruktur erreichen lässt).
# Rotierte PCA
pca.3.rotiert <- principal(lifesat, nfactors = 3, rotate = "varimax")
# Per Default ist das principal-Objekt nicht sortiert. Damit wir die
# Items in der Reihenfolge der Faktorenladungen bekommen, müssen wir
# die Funktion `print.psych()` auf das Objekt anwenden und den
# Parameter `sort = TRUE` setzen.
print.psych(pca.3.rotiert, sort = TRUE)Principal Components Analysis
Call: principal(r = lifesat, nfactors = 3, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrix
item RC1 RC3 RC2 h2 u2 com
leben6_selbst 5 0.78 0.13 -0.01 0.63 0.37 1.1
leben2_selbst 4 0.76 -0.05 0.10 0.58 0.42 1.0
leben5_freunde 6 0.70 0.16 0.14 0.54 0.46 1.2
leben7_freunde 7 0.57 0.18 0.02 0.36 0.64 1.2
leben9_familie 9 0.05 0.88 0.07 0.78 0.22 1.0
leben8_familie 8 0.12 0.83 0.08 0.71 0.29 1.1
leben10_familie 10 0.21 0.62 0.14 0.44 0.56 1.3
leben4_schule 3 0.14 0.03 0.85 0.75 0.25 1.1
leben3_schule 2 0.01 0.03 0.82 0.68 0.32 1.0
leben1_schule 1 0.06 0.24 0.58 0.40 0.60 1.4
RC1 RC3 RC2
SS loadings 2.08 1.99 1.80
Proportion Var 0.21 0.20 0.18
Cumulative Var 0.21 0.41 0.59
Proportion Explained 0.35 0.34 0.31
Cumulative Proportion 0.35 0.69 1.00
Mean item complexity = 1.1
Test of the hypothesis that 3 components are sufficient.
The root mean square of the residuals (RMSR) is 0.1
with the empirical chi square 211.22 with prob < 5.6e-35
Fit based upon off diagonal values = 0.85Die Reihenfolge der Darstellung der rotierten Komponenten (RC) ergibt sich aus der Grösse der Eigenwerte/des Varianzanteils nach der Rotation. Jetzt ist der Anteil der erklärten Varianz der drei Komponenten sehr ähnlich, da durch die Rotation das Kriterium der sukzessiv maximalen Varianzaufklärung aufgehoben wurde und die erklärte Varianz mit dem Ziel einer Einfachstruktur möglichst gleichmässig auf die Komponenten verteilt wurde.
Wir können aufgrund folgender Tabelle beispielhaft nochmal einen rotierten Eigenwert von Hand berechnen, diesmal den der ersten Komponente:
| RC1 | RC3 | RC2 | |
|---|---|---|---|
| leben1_schule | 0.057 | 0.243 | 0.578 |
| leben3_schule | 0.014 | 0.031 | 0.823 |
| leben4_schule | 0.139 | 0.027 | 0.854 |
| leben2_selbst | 0.756 | -0.052 | 0.102 |
| leben6_selbst | 0.784 | 0.127 | -0.015 |
| leben5_freunde | 0.701 | 0.163 | 0.143 |
| leben7_freunde | 0.569 | 0.178 | 0.018 |
| leben8_familie | 0.124 | 0.833 | 0.076 |
| leben9_familie | 0.048 | 0.880 | 0.075 |
| leben10_familie | 0.206 | 0.617 | 0.142 |
\(~\)
\(\begin{aligned} Var(H_{1 rotiert}) &= \lambda_{11}^2 + \lambda_{21}^2 + \lambda_{31}^2 + \lambda_{41}^2 + \lambda_{51}^2 + \lambda_{61}^2 + \lambda_{71}^2 + \lambda_{81}^2 + \lambda_{91}^2 + \lambda_{101}^2 \\ &= 0.057^2 + 0.014^2 + 0.139^2 + 0.756^2 + 0.784^2 + 0.701^2 + 0.569^2 + 0.124^2 \\ &{~~~~~}+ 0.048^2 + 0.206^2 \\ &= 2.084 \end{aligned}\)
\(~\)
Daraus folgender Anteil der erklärten Varianz der ersten rotierten Komponente:
Proportion Var \(= \frac{2.084}{10} = 0.2084\)
Die Kommunalität der Items bleibt nach orthogonaler Rotation dagegen unverändert, z.B. für leben2_selbst:
\(\begin{aligned} \hat{H}(Y_4) &= \lambda_{41}^2 + \lambda_{42}^2 + \lambda_{43}^2 \\ &= 0.756^2 + (-0.052)^2 + 0.102^2 \\ &= 0.58 \end{aligned}\)
\(~\)
Tatsächlich gibt es jetzt weniger und deutlich schwächere Querladungen. Entsprechend ist auch die com (Komplexität) der Items gesunken. Jetzt erst zeigt sich eine Einfachstruktur und damit auch, wie die Komponenten inhaltlich zu interpretieren sind: auf der ersten rotierten Komponente (RC1) laden die Items der Inhaltsbereiche Selbst und Freunde, die zweite rotierte Komponente (RC2) ist als Schul-Komponente zu interpretieren und die dritte (RC3) als Familien-Komponente.
Es gibt nur wenige Querladungen, und diese liegen alle unter dem empfohlenen Cutoff von |0.30|. leben10_familie hat eine Ladung von 0.21 auf der Selbst/Freunde-Komponente und leben1_schule hat eine Ladung von 0.24 auf der Familien-Komponente. Alle anderen Ladungen auf nicht zugehörigen Komponenten sind < 0.20.
4.5 Oblique Rotation mit drei Hauptkomponenten
Jetzt benutzen wir als oblique Rotation eine Oblimin-Rotation. Je stärker die Komponenten (tatsächlich) miteinander korrellieren, desto grösser ist der Vorteil von obliquen Rotationen. Diese können anders als orthogonale Rotationen eine Korrelation der latenten Variablen (Komponenten) selbst abbilden und damit bei den Ladungen (die jetzt nicht mehr als Korrelationen, sondern als Partial-Regressionskoeffizienten zu interpretieren sind) eine noch bessere Einfachstruktur erreichen. Falls die Dimensionen tatsächlich orthogonal sein sollten, so wird sich das in Komponentenkorrelationen nahe Null widerspiegeln. Das ist auch der Grund, warum man orthogonale Rotationen nur in seltenen Fällen wirklich benötigt.
# Oblique Rotation
pca.3.rotiert.obli <- principal(lifesat, nfactors = 3, rotate = "oblimin")
# Sortiert ausgeben lassen:
print.psych(pca.3.rotiert.obli, sort = TRUE)Principal Components Analysis
Call: principal(r = lifesat, nfactors = 3, rotate = "oblimin")
Standardized loadings (pattern matrix) based upon correlation matrix
item TC1 TC3 TC2 h2 u2 com
leben6_selbst 5 0.79 0.05 -0.08 0.63 0.37 1.0
leben2_selbst 4 0.77 -0.14 0.05 0.58 0.42 1.1
leben5_freunde 6 0.69 0.09 0.08 0.54 0.46 1.1
leben7_freunde 7 0.56 0.12 -0.04 0.36 0.64 1.1
leben9_familie 9 -0.05 0.90 -0.01 0.78 0.22 1.0
leben8_familie 8 0.03 0.84 -0.01 0.71 0.29 1.0
leben10_familie 10 0.13 0.60 0.07 0.44 0.56 1.1
leben4_schule 3 0.06 -0.03 0.86 0.75 0.25 1.0
leben3_schule 2 -0.06 -0.01 0.83 0.68 0.32 1.0
leben1_schule 1 -0.02 0.21 0.56 0.40 0.60 1.3
TC1 TC3 TC2
SS loadings 2.08 2.00 1.79
Proportion Var 0.21 0.20 0.18
Cumulative Var 0.21 0.41 0.59
Proportion Explained 0.35 0.34 0.30
Cumulative Proportion 0.35 0.70 1.00
With component correlations of
TC1 TC3 TC2
TC1 1.00 0.22 0.18
TC3 0.22 1.00 0.17
TC2 0.18 0.17 1.00
Mean item complexity = 1.1
Test of the hypothesis that 3 components are sufficient.
The root mean square of the residuals (RMSR) is 0.1
with the empirical chi square 211.22 with prob < 5.6e-35
Fit based upon off diagonal values = 0.85Gibt es noch Querladungen? - Das einzige Item, das noch eine geringfügige Querladung aufweist, ist leben1_schule. Dieses bezieht sich direkt auf die Schulnoten und zeigt eine Querladung von 0.21 auf der Familien-Komponente (TC3). Auch ist die Ladung dieses Items auf der Schulkomponente (TC2) deutlich niedriger als die der anderen beiden zugehörigen Items. Die Schulnoten scheinen also auch für die Zufriedenheit für den Bereich Familie eine gewisse Bedeutung zu haben. Das ist inhaltlich durchaus nachvollziehbar.
In Bezug auf die Komponentenkorrelationen zeigt sich, dass alle drei Komponenten relativ gleichmässig und gleichzeitig nicht sonderlich stark miteinander korrelieren \((r_{H_1H_2} = 0.18, r_{H_1H_3} = 0.22, r_{H_2H_3} = 0.17)\). Dies kann auf eine übergeordnete Dimension Lebenszufriedenheit hinweisen. Damit werden wir uns demnächst bei der konfirmatorischen Faktorenanalyse (CFA) noch weiter beschäftigen.
Visualisierung:
Wie stark die Items auf Komponenten laden, kann mit factor.plot() dargestellt werden:
factor.plot(pca.3.rotiert.obli, cut = 0.5)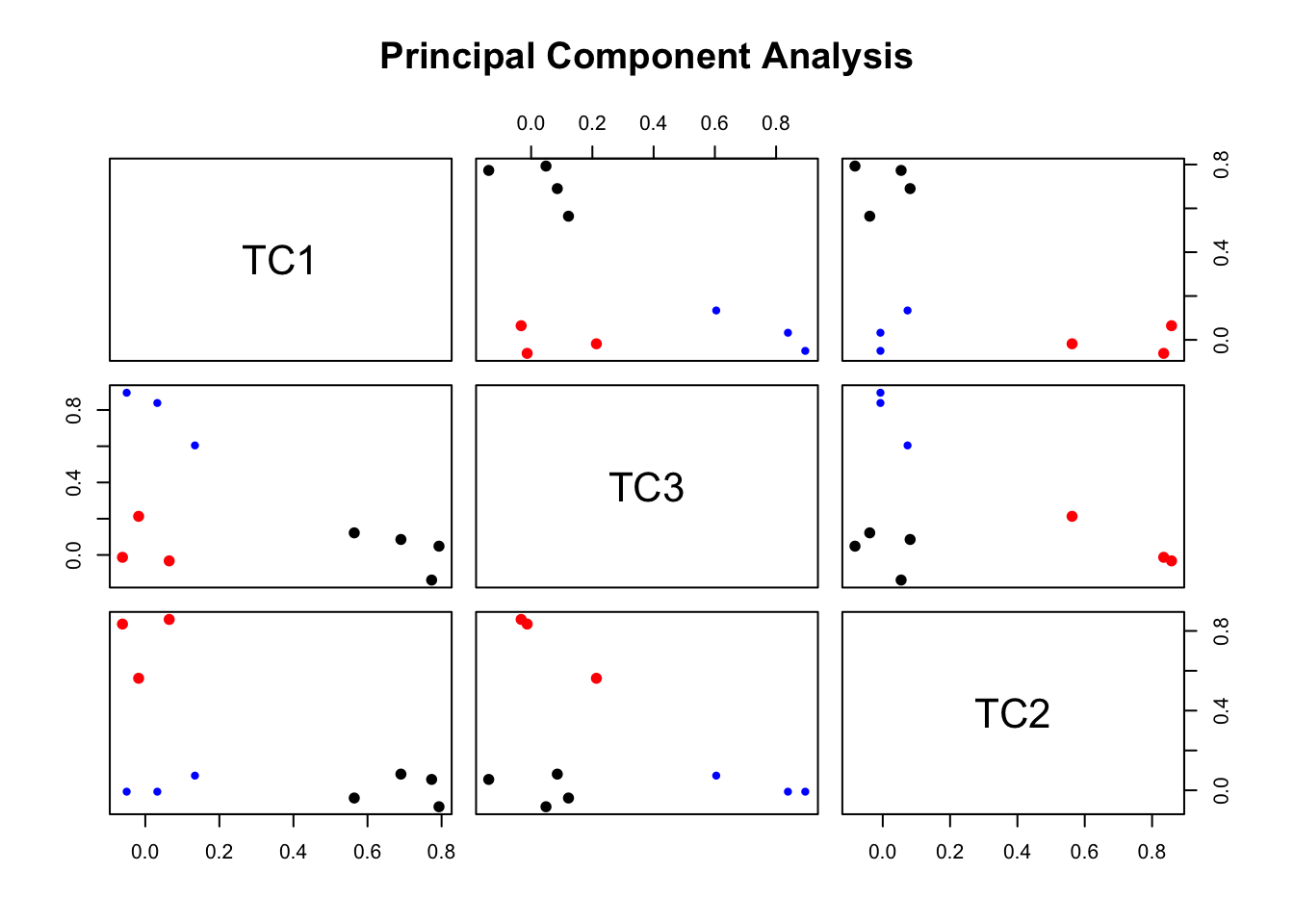
\(~\)
Welche Items “gehören” zu welcher Komponente? Das können wir mit fa.diagram() darstellen:
fa.diagram(pca.3.rotiert.obli)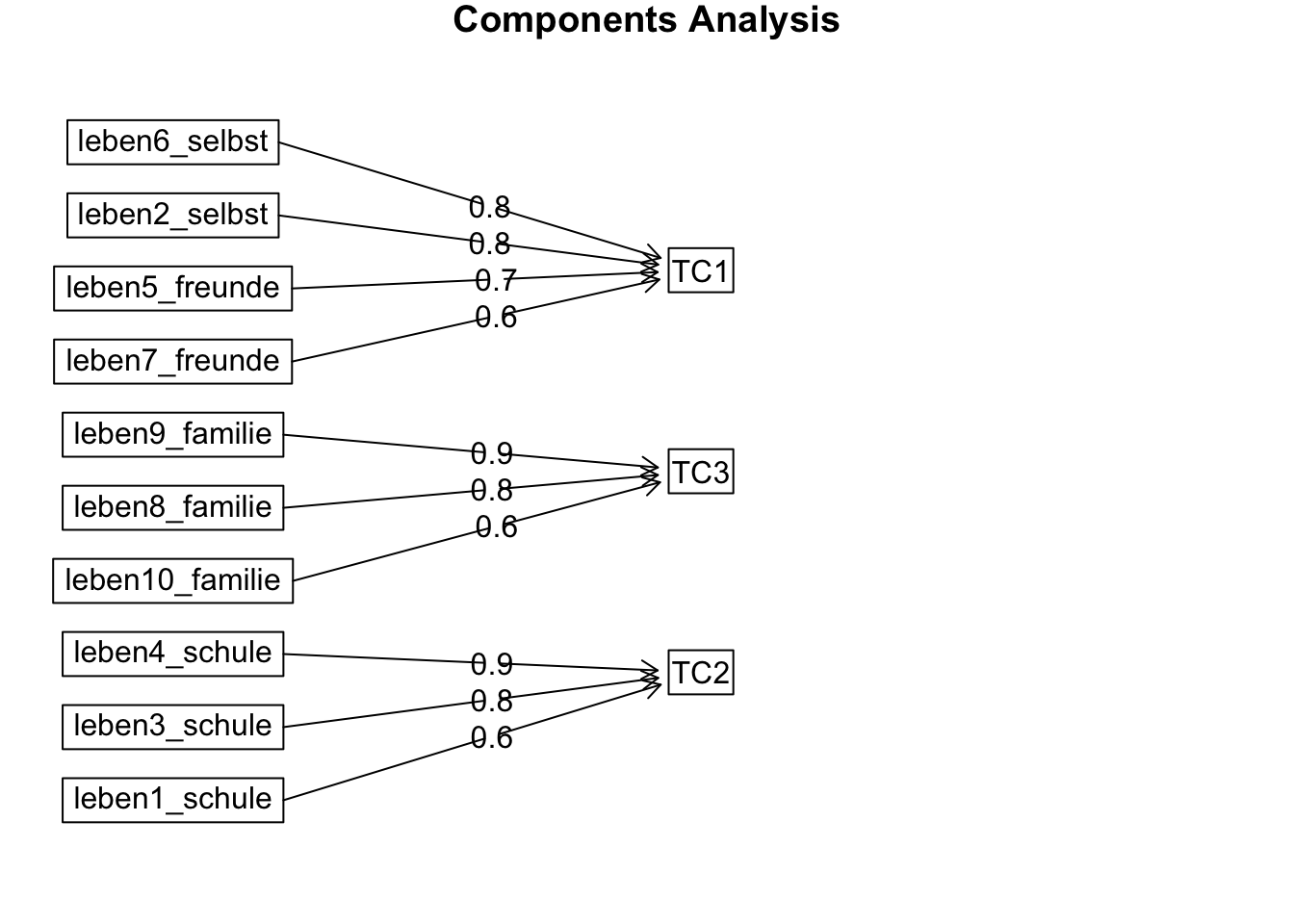
4.6 Zusammenfassung PCA
Die PCA zeigt also, dass drei Hauptkomponenten insgesamt ca. 60 % der Gesamtvarianz erklären können und dass diese im Vergleich zu den übrigen sieben Komponenten über eine überdurchschnittliche Varianzaufklärung verfügen. Ob dies auch im Sinne einer EFA, die die Korrelationen zwischen den Items vollständig durch Faktoren erkären will, ausreicht, wird sich im nächsten Teil zeigen.
Inhaltlich interessant ist die Kombination der Lebenzufriedenheit mit dem Bereich Selbst und dem Bereich Freunde. Diese beiden Zufriedenheiten scheinen eng miteinander verknüpft zu sein.
Eine gute Visualisierung und noch etwas mehr Intuition gibts in diesem Applet.