pacman::p_load(lme4, nlme, tidyverse, lmerTest, gridExtra, ggplot2)1 Modelle mit Level-1-Prädiktoren
In diesem Kapitel behandeln wir Hierarchische Lineare Modelle mit Level-1-Prädiktoren. Aufbau und Systematik der Darstellung orientieren sich am Lehrbuch “Statistik und Forschungsmethoden” von Eid et al. (2017).
Es handelt sich um Modelle mit einer 2-Ebenen-Struktur (Individuen genestet in Gruppen), und zunächst werden nur Modelle ohne jede Prädiktorvariable (Intercept-Only-Modell) sowie Modelle mit ausschliesslich Prädiktorvariablen auf Level 1 (Random-Intercept-Modell und Random-Coefficients-Modell) behandelt.
Laden der benötigten Packages:
1.1 HLM Packages
Zu Beginn ein kurzer Überblick über die beiden Packages, die wir in diesem Kurs für Hierarchische Lineare Modelle benutzen werden.
nlme
Dies ist das ursprüngliche HLM- oder Mixed-Model-Package. Es hat mehr Optionen, insbesondere im Hinblick auf die Struktur der Level-1-Fehler bei Daten mit wiederholten Messungen. Wir verwenden nlme im Kapitel zu HLM-Modellen mit Messwiederholung. Die Syntax-Struktur wird dort behandelt.
lme4
Dieses modernere HLM-Package ist sehr gut geeignet für “normale” Hierarchische Lineare Modelle mit genesteten Gruppen. Wir verwenden es im Folgenden für die Analysen der Modelle mit Level-1- und Level-2-Prädiktoren.
Die “lme4”-Syntax baut auf der model syntax auf, die wir schon von lm() für “normale” Regressionsmodelle kennen. Also:
lm(formula = AbhängigeVariable ~ UnabhängigeVariable, data = dataframe)
Bei der Funktion lmer() (aus dem Package lme4) kommt die Spezifizierung der Gruppenvariable hinzu, und welche zufälligen Effekte geschätzt werden sollen. Die Syntax in der Klammer unterscheidet die lmer()-Syntax von der simplen Syntax der lm()-Funktion. In der Klammer wird links vom | spezifiziert, welche zufälligen Effekte geschätzt werden sollen. Rechts des | steht die Variable, die die Gruppenstruktur (Nestungsstruktur) der Daten definiert.
Eine 1 im linken Teil der Klammer bedeutet, dass Random Intercepts geschätzt werden sollen. Wenn die Unabhängige Variable (also die Prädiktorvariable) auch links vor dem | steht, bedeutet dies, dass zusätzlich auch Random Slopes geschätzt werden.
Was bedeutet also folgende Syntax?
lmer(data = dataframe, AbhängigeVariable ~ UnabhängigeVariable + (1 | Gruppenvariable))
Antwort: die Abhängige Variable (AV) wird durch die Unabhängige Variable (UV) vorhergesagt. Gleichzeitig wird der Intercept separat für jede Ausprägung der Gruppenvariable geschätzt bzw. die Varianz der Level-2-Residuen des Intercepts ist ein Parameter des Modells.
Diese Syntax wird später noch erweitert.
1.2 Daten laden und aufbereiten
Wir laden die Daten und speichern sie im Objekt df (für “data frame”). Wir können das Datenfile direkt aus dem Internet (GitHub) herunterladen:
df <- read_csv(
url("https://raw.githubusercontent.com/methodenlehre/data/master/statistik_IV/salary-data.csv")
)1.2.1 Beschreibung der Beispieldaten
Bei diesen Daten handelt es sich um Lohn-Daten von 20 Firmen mit je 30 Angestellten (fiktive, simulierte Daten). Zu jeder/jedem Angestellten haben wir Informationen zum Lohn (salary, in 1000 CHF), bei welcher Firma die Person angestellt ist (company), und wie lange die Person schon dort arbeitet (experience). Ausserdem haben wir noch Informationen darüber, in welchem Sektor (Private oder Public) die Firma tätig ist (sector). Mit dieser Variable beschäftigen wir uns aber erst in Kapitel 2.
Bevor wir uns die Daten anschauen, müssen company und sector noch als Faktoren definiert werden.
df <- df |>
mutate(
company = as.factor(company),
sector = as.factor(sector)
)Jetzt können wir uns den Daten-Frame anschauen:
# Die Funktion "tail()" gibt uns die letzten 6 Zeilen aus.
tail(df)# A tibble: 6 × 4
company experience salary sector
<fct> <dbl> <dbl> <fct>
1 Company 20 3.58 6.84 Private
2 Company 20 3.18 7.60 Private
3 Company 20 3.39 5.71 Private
4 Company 20 7.12 10.1 Private
5 Company 20 2.98 6.94 Private
6 Company 20 6.45 9.33 Private# Die Funktion summary() gibt uns deskriptive Statistiken
# zum Datensatz aus.
summary(df) company experience salary sector
Company 01: 30 Min. : 0.000 Min. : 4.587 Private:300
Company 02: 30 1st Qu.: 4.027 1st Qu.: 7.602 Public :300
Company 03: 30 Median : 5.170 Median : 8.564
Company 04: 30 Mean : 5.190 Mean : 8.738
Company 05: 30 3rd Qu.: 6.402 3rd Qu.: 9.840
Company 06: 30 Max. :10.000 Max. :15.418
(Other) :420 1.2.2 Group-centering des Level-1-Prädiktors experience
In diesem Kapitel zu Modellen mit Level-1-Prädiktoren werden wir uns hauptsächlich mit dem Effekt des Level-1-Prädiktors experience auf die AV salary beschäftigen. Dabei geht es zum einen darum, wie gross der durchschnittliche Effekt von experience ist, das heisst der Effekt innerhalb der Firmen gemittelt über alle Firmen hinweg. Das ist die grundsätzliche Logik von HLM-Modellen (simultane Schätzung eines Regressionseffekts innerhalb mehrerer Gruppen und dann Mittelung dieses Effekts über die Gruppen hinweg). Zum anderen geht es darum, wie stark diese “Innerhalb-Effekte” zwischen den Gruppen variieren, also wie ähnlich bzw. unterschiedlich der Effekt von experience auf salary in den verschiedenen Gruppen ist.
Man könnte diese Modelle mit der Original-Variablen experience als Level-1-UV schätzen (vgl. das Vorgehen bei Eid et al. (2017)). Es ist jedoch für bestimmte Aspekte der Modelle (insbesondere für spätere Modelle mit Level-2-Prädiktoren, die wir in Kapitel 2 betrachten werden) sinnvoll, wenn wir für den Level-1-Prädiktor experience vorher ein “Group-centering” vornehmen, d.h. die Abweichung jeder Person von ihrem Gruppenmittelwert berechnen und diese in der Variablen exp_centered speichern.
exp_centered enthält also nur noch Informationen darüber, wieviel mehr (positiver Wert) oder weniger (negativer Wert) Erfahrung eine Person relativ zum experience-Mittelwert ihrer Firma aufweist. Wir benutzen in diesem und im nächsten Kapitel ausschliesslich diese gruppenzentrierte Variable exp_centered als Level-1-Prädiktor.
Wir berechnen exp_centered mit der Pipe |> und benutzen group_by() und mutate() aus dem tidyverse-Package. Um die Berechnung durchzuführen, berechnen wir zuerst eine Gruppenmittelwerts-Variable exp_groupmean, die wir später in Kapitel 2 noch brauchen werden und aus diesem Grund im Datensatz behalten.
# Berechnen der experience-Mittelwerte pro Gruppe (exp_groupmean),
# und der Gruppenmittelwert-zentrierten experience (exp_centered)
df <- df |>
group_by(company) |>
mutate(
exp_groupmean = mean(experience),
exp_centered = experience - exp_groupmean
) |>
ungroup()
# Jetzt können wir uns die Daten nochmals anschauen - hat alles funktioniert?
head(df)# A tibble: 6 × 6
company experience salary sector exp_groupmean exp_centered
<fct> <dbl> <dbl> <fct> <dbl> <dbl>
1 Company 01 6.87 8.96 Private 6.37 0.496
2 Company 01 5.66 9.54 Private 6.37 -0.714
3 Company 01 4.58 7.30 Private 6.37 -1.79
4 Company 01 6.56 8.09 Private 6.37 0.186
5 Company 01 8.83 14.3 Private 6.37 2.46
6 Company 01 7.73 10.3 Private 6.37 1.36 tail(df)# A tibble: 6 × 6
company experience salary sector exp_groupmean exp_centered
<fct> <dbl> <dbl> <fct> <dbl> <dbl>
1 Company 20 3.58 6.84 Private 5.04 -1.46
2 Company 20 3.18 7.60 Private 5.04 -1.86
3 Company 20 3.39 5.71 Private 5.04 -1.65
4 Company 20 7.12 10.1 Private 5.04 2.08
5 Company 20 2.98 6.94 Private 5.04 -2.06
6 Company 20 6.45 9.33 Private 5.04 1.411.3 Intercept-Only-Modell (Modell 1)
In diesem Modell ist noch keine Prädiktorvariable enthalten, es handelt sich also um eine Art Nullmodell, das nur die Variation des Achsenabschnitts zwischen den Gruppen modelliert. Und in einem Modell ohne Prädiktor beziehen sich die gruppenspezifischen Intercepts \(\beta_{0i}\) auf die Gruppenmittelwerte der AV salary (in diesem Fall der 20 Firmen).
Level-1-Modell: \(\boldsymbol {y_{mi}=\beta_{0i}+\varepsilon_{mi}}\)
Level-2-Modell: \(\boldsymbol {\beta_{0i}=\gamma_{00} + \upsilon_{0i}}\)
Gesamtmodell: \(\boldsymbol {y_{mi} = \gamma_{00} + \upsilon_{0i}+\varepsilon_{mi}}\)
1.3.1 Modell berechnen
# Fitten des Modells und Abspeichern in der Variable intercept.only.model
intercept.only.model <- lmer(salary ~ 1 + (1 | company), data = df, REML = TRUE)
# Abspeichern von Prädiktionen, die dieses Modell macht.
# In diesem Falle ist dies jeweils der durchschnittliche Lohn jeder Firma
# Die Funktion predict() gibt pro Zeile (in diesem Fall pro Angestelltem)
# eine Prädiktion aus, je nachdem, in welcher Firma die Person angestellt ist.
# Wir speichern diese vorhergesagten Werte, um das Modell später mit "ggplot2"
# zu veranschaulichen.
df$intercept.only.preds <- predict(intercept.only.model)
# Output anschauen
summary(intercept.only.model)Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: salary ~ 1 + (1 | company)
Data: df
REML criterion at convergence: 2158
Scaled residuals:
Min 1Q Median 3Q Max
-2.9816 -0.6506 -0.0494 0.5779 4.2131
Random effects:
Groups Name Variance Std.Dev.
company (Intercept) 0.8512 0.9226
Residual 1.9547 1.3981
Number of obs: 600, groups: company, 20
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 8.7376 0.2141 19.0000 40.82 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Mit der Funktion ranef() kann man sich die einzelnen Random-Effects (Level-2-Residuen des Intercepts, also die \(\upsilon_{0i}\)) ausgeben lassen:
ranef(intercept.only.model)$company
(Intercept)
Company 01 0.78965416
Company 02 1.10501807
Company 03 1.92302618
Company 04 -1.13650080
Company 05 0.95354595
Company 06 -0.95893185
Company 07 -0.01014627
Company 08 -0.25484048
Company 09 -0.65131802
Company 10 0.76848590
Company 11 -0.50626620
Company 12 0.94040709
Company 13 -0.74284383
Company 14 -0.97545482
Company 15 -1.16136931
Company 16 -0.09768008
Company 17 0.66196052
Company 18 -0.16811195
Company 19 0.35123926
Company 20 -0.82987351
with conditional variances for "company" 1.3.2 Intraklassenkorrelation
Die Intraklassenkorrelation quantifiziert das Ausmass der „Nicht-Unabhängigkeit” zwischen den Messwerten aufgrund systematischer Level-2-Unterschiede im gemessenen Merkmal. Je grösser der Anteil der Level-2-Varianz (Varianz der Gruppenmittelwerte) an der Gesamtvarianz (Summe der Level-2-Varianz und der Level-1-Varianz), desto grösser sind die Ähnlichkeiten innerhalb der Level-2-Einheiten im Vergleich zu zwischen den Level-2-Einheiten.
Die Intraklassenkorrelation ist definiert als: \(\boldsymbol {\rho = \frac{\sigma^2_{Level-2}}{\sigma^2_{Level-2}+ \sigma^2_{Level-1}}}\)
Die Intraklassenkorrelation erhält man bei Schätzung eines Nullmodells (Intercept-Only-Modell, s.o.), bei dem sowohl die (zufällige) Varianz des Intercepts (in einem Modell ohne Prädiktoren also die Varianz der Mittelwerte der Level-2-Einheiten) als auch die Level-1-Residualvarianz ausgegeben wird.
Wenn die Level-2-Varianz sich nicht überzufällig von 0 unterscheidet, spielen die Ähnlichkeiten/Abhängigkeiten innerhalb der Level-2-Einheiten keine Rolle und ein Mehrebenenmodell ist nicht unbedingt notwendig.
Intraklassenkorrelation: \(\hat{\rho} = \frac{\hat{\sigma}^2_{\upsilon_0}}{\hat{\sigma}^2_{\upsilon_0}+ \hat{\sigma}^2_\varepsilon} = \frac {0.8512}{0.8512+1.9547} = 0.303\)
-> ca. 30 % der Gesamtvarianz sind auf Level-2-(Firmen-)Unterschiede zurückzuführen.
1.3.3 Signifikanztest
Signifikanztest für \(\sigma^2_{\upsilon_0}\): Modellvergleich mit absolutem Nullmodell
Wir kennen nun also die Level-2-Varianz, aber wir haben noch keinen Signifikanztest für diesen Parameter. Diesen erhalten wir über einen Modellvergleich (Likelihood-Ratio-Test) des Intercept-Only-Modells mit einem Modell, dass keinen Random-Intercept enthält, d.h. mit einem “normalen” linearen Modell ohne Prädiktor (mit dem Gesamt-Mittelwert \(\gamma_{00}\) als einzigem Modellparameter neben der Level-1-Residualvarianz \(\sigma^2_\varepsilon\)). Dieses Modell kann man auch als “absolutes Nullmodell” bezeichnen. Wir müssen ein solches Modell nicht extra spezifizieren, sondern können die Funktion ranova() auf das Outputobjekt intercept.only.model anwenden. ranova() (aus dem lme4-Hilfspackage lmerTest) führt automatisch Modellvergleiche (nur) für Random-Effects durch, indem die vorhandenen Random-Effects Schritt für Schritt entfernt werden und das Ausgangsmodell dann mit dem so reduzierten Modell verglichen wird. In diesem Fall (Intercept-Only-Modell als Ausgangsmodell) kann nur ein Random-Effect entfernt werden, nämlich der des Intercepts.
# Vergleich des Intercept-Only-Modells mit dem "absoluten Nullmodell"
ranova(intercept.only.model)ANOVA-like table for random-effects: Single term deletions
Model:
salary ~ (1 | company)
npar logLik AIC LRT Df Pr(>Chisq)
<none> 3 -1079.0 2164.0
(1 | company) 2 -1157.7 2319.4 157.44 1 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Vergleich ist signifikant \((p<0.001)\). Wir können den p-Wert sogar noch halbieren, da es sich um einen einseitigen Test handelt. Der zu testende Parameter \(\sigma^2_{\upsilon_0}\) weist nämlich einen bounded parameter space auf (kann nicht kleiner als 0 werden). Damit haben wir eine signifikante Level-2-Varianz des Intercepts und die Verwendung eines hierarchischen linearen Modells für die folgenden Analysen ist damit angezeigt.
Weiter unten werden wir zeigen, wie Modellvergleiche mittels Likelihood-Ratio-Test auch von Hand durchgeführt werden können.
Visuell kann man sich den Vergleich zwischen dem absoluten Nullmodell und dem Intercept-Only-Modell folgendermassen vorstellen:
Code
xlabel <- "Experience in years (deviation from company mean)"
ylabel <- "Salary per month"
# Visual comparison between the two models
null.model <- lm(salary ~ 1, data = df)
df$null.model.preds <- predict(null.model)
ggplot(data = df, aes(x = exp_centered, y = null.model.preds)) + # , group=groupVar, colour=groupVar))+
geom_smooth(method = "lm", fullrange = TRUE, se = F, linewidth = .3) +
geom_jitter(aes(y = salary, colour = company), alpha = .2) +
labs(x = xlabel, y = ylabel) +
ggtitle("Absolutes Nullmodell") +
scale_colour_discrete() +
ggthemes::theme_tufte()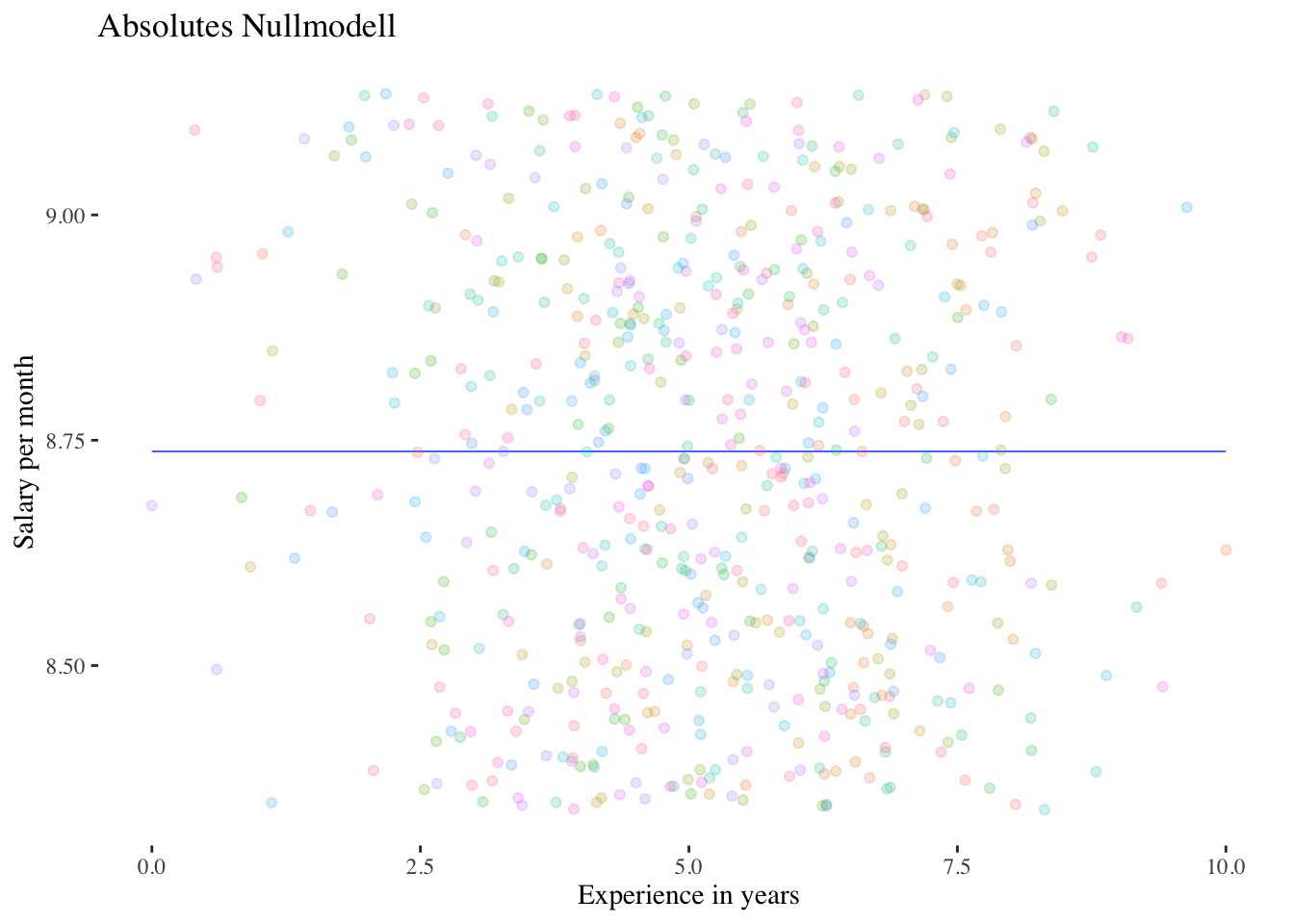
Code
df$intercept.only.preds <- predict(intercept.only.model)
ggplot(data = df, aes(
x = exp_centered,
y = intercept.only.preds,
colour = company
)) +
geom_smooth(method = "lm", fullrange = TRUE, se = F, size = .3) +
geom_jitter(aes(y = salary), alpha = .2) +
labs(x = xlabel, y = ylabel) +
ggtitle("Intercept-Only-Modell") +
scale_colour_discrete() +
geom_abline(intercept = fixef(intercept.only.model), slope = 0) +
ggthemes::theme_tufte()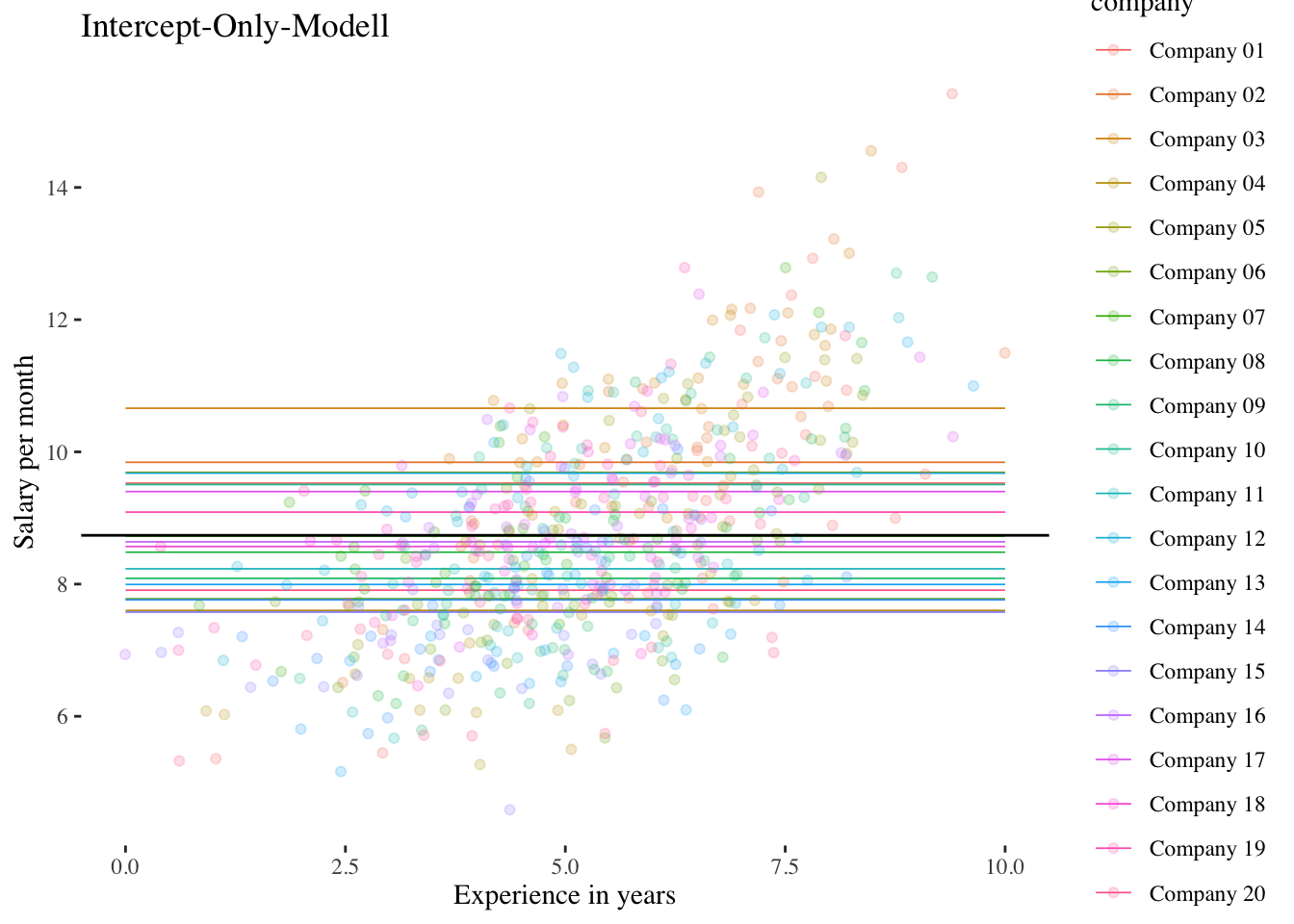
Vertiefung: Shrinkage
Wir haben oben bereits angemerkt, dass in einem Intercept-Only-Modell die Gruppen-Intercepts den salary Firmenmittelwerten “entsprechen”. Die geschätzten Gruppenmittelwerte \((\hat\gamma_{00} + \upsilon_{0i})\) erhält man mit coef(). Vergleichen wir diese mit den empirischen Durchschnittsgehältern pro Firma:
est_means <- coef(intercept.only.model)$company[, 1]
emp_means <- df |>
group_by(company) |>
summarise(emp_means = mean(salary)) |>
ungroup() |>
dplyr::select(emp_means)
salary <- tibble(est_means, emp_means) |>
mutate(diff_means = est_means - emp_means)
salary# A tibble: 20 × 3
est_means emp_means diff_means
<dbl> <dbl> <dbl>
1 9.53 9.59 -0.0604
2 9.84 9.93 -0.0846
3 10.7 10.8 -0.147
4 7.60 7.51 0.0870
5 9.69 9.76 -0.0730
6 7.78 7.71 0.0734
7 8.73 8.73 0.000777
8 8.48 8.46 0.0195
9 8.09 8.04 0.0499
10 9.51 9.56 -0.0588
11 8.23 8.19 0.0388
12 9.68 9.75 -0.0720
13 7.99 7.94 0.0569
14 7.76 7.69 0.0747
15 7.58 7.49 0.0889
16 8.64 8.63 0.00748
17 9.40 9.45 -0.0507
18 8.57 8.56 0.0129
19 9.09 9.12 -0.0269
20 7.91 7.84 0.0635 Man kann erkennen, dass die geschätzten Intercepts pro Firma nicht mit den tatsächlichen empirischen Gruppenmitteln übereinstimmen. In einem Mehrebenenmodell werden diese Schätzungen mit “Shrinkage” (Schrumpfung) berechnet, d.h. sie werden in Richtung des Gesamtmittelwertes “gezogen”. Dies liegt daran, dass die Level-2-Residuen in diesem Modell als normalverteilt angenommen werden und die Schätzunsicherheit in dem Sinne berücksichtigt wird, dass die Firmenmittelwerte der AV salary durch Gewichtung (“Pooling”) mit dem Gesamtmittelwert korrigiert werden, um zu den Estimates \(\beta_{0i}=\hat\gamma_{00} + \upsilon_{0i}\) zu gelangen.
Dies ist auch der Grund, warum Mehrebenenmodelle manchmal als “Partial-Pooling-Modelle” bezeichnet werden (z.B. bei Gelman & Hill, 2007), im Gegensatz zu “No-Pooling-Modellen” (lineare Modelle mit Gruppen als fixed effects ohne jegliche Annahmen bezüglich der Varianz auf Ebene 2).
Schauen wir uns zum Vergleich ein solches “No-Pooling-Modell” an:
no.pooling <- lm(salary ~ company, data = df)
summary(no.pooling)
Call:
lm(formula = salary ~ company, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.2291 -0.8918 -0.0401 0.7795 5.8300
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.58770 0.25526 37.560 < 2e-16 ***
companyCompany 02 0.33950 0.36099 0.940 0.347369
companyCompany 03 1.22013 0.36099 3.380 0.000774 ***
companyCompany 04 -2.07359 0.36099 -5.744 1.49e-08 ***
companyCompany 05 0.17644 0.36099 0.489 0.625201
companyCompany 06 -1.88243 0.36099 -5.215 2.57e-07 ***
companyCompany 07 -0.86102 0.36099 -2.385 0.017393 *
companyCompany 08 -1.12444 0.36099 -3.115 0.001931 **
companyCompany 09 -1.55127 0.36099 -4.297 2.03e-05 ***
companyCompany 10 -0.02279 0.36099 -0.063 0.949687
companyCompany 11 -1.39512 0.36099 -3.865 0.000124 ***
companyCompany 12 0.16229 0.36099 0.450 0.653188
companyCompany 13 -1.64980 0.36099 -4.570 5.96e-06 ***
companyCompany 14 -1.90022 0.36099 -5.264 1.99e-07 ***
companyCompany 15 -2.10036 0.36099 -5.818 9.84e-09 ***
companyCompany 16 -0.95525 0.36099 -2.646 0.008362 **
companyCompany 17 -0.13747 0.36099 -0.381 0.703488
companyCompany 18 -1.03108 0.36099 -2.856 0.004441 **
companyCompany 19 -0.47197 0.36099 -1.307 0.191585
companyCompany 20 -1.74349 0.36099 -4.830 1.75e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.398 on 580 degrees of freedom
Multiple R-squared: 0.3154, Adjusted R-squared: 0.293
F-statistic: 14.06 on 19 and 580 DF, p-value: < 2.2e-16Das Modell ohne Pooling entspricht einem ANOVA-Modell, und die Effekte vergleichen die Lohn-Mittelwerte der Firmen 02-20 mit dem von Firma 01 (d.h. Effekte von dummy-codierten Variablen mit Firma 01 als Referenzkategorie). Das \(R^2\) dieses Modells mit festen Effekten (fixed effects ANOVA) ist etwas höher als die Intraklassen-Korrelation des Intercept-Only-Modells (0.3154 vs. 0.3034), was eben die im Mehrebenenmodell vorhandene Shrinkage widerspiegelt.
Um ein Modell mit Schätzungen für alle Unternehmensmittelwerte (statt der Dummy-Effekte) zu erhalten, können wir den Intercept des lm()-Modells weglassen:
no.pooling2 <- lm(salary ~ company - 1, data = df)
summary(no.pooling2)
Call:
lm(formula = salary ~ company - 1, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.2291 -0.8918 -0.0401 0.7795 5.8300
Coefficients:
Estimate Std. Error t value Pr(>|t|)
companyCompany 01 9.5877 0.2553 37.56 <2e-16 ***
companyCompany 02 9.9272 0.2553 38.89 <2e-16 ***
companyCompany 03 10.8078 0.2553 42.34 <2e-16 ***
companyCompany 04 7.5141 0.2553 29.44 <2e-16 ***
companyCompany 05 9.7641 0.2553 38.25 <2e-16 ***
companyCompany 06 7.7053 0.2553 30.19 <2e-16 ***
companyCompany 07 8.7267 0.2553 34.19 <2e-16 ***
companyCompany 08 8.4633 0.2553 33.16 <2e-16 ***
companyCompany 09 8.0364 0.2553 31.48 <2e-16 ***
companyCompany 10 9.5649 0.2553 37.47 <2e-16 ***
companyCompany 11 8.1926 0.2553 32.09 <2e-16 ***
companyCompany 12 9.7500 0.2553 38.20 <2e-16 ***
companyCompany 13 7.9379 0.2553 31.10 <2e-16 ***
companyCompany 14 7.6875 0.2553 30.12 <2e-16 ***
companyCompany 15 7.4873 0.2553 29.33 <2e-16 ***
companyCompany 16 8.6324 0.2553 33.82 <2e-16 ***
companyCompany 17 9.4502 0.2553 37.02 <2e-16 ***
companyCompany 18 8.5566 0.2553 33.52 <2e-16 ***
companyCompany 19 9.1157 0.2553 35.71 <2e-16 ***
companyCompany 20 7.8442 0.2553 30.73 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.398 on 580 degrees of freedom
Multiple R-squared: 0.9761, Adjusted R-squared: 0.9753
F-statistic: 1185 on 20 and 580 DF, p-value: < 2.2e-16Nebenbemerkung: Da das Modell keinen Intercept enthält, beinhaltet die F-Statistik des Modells nun auch den Test der Gruppenmittelwerte gegen 0, so dass wir sie nicht für den Vergleich der Lohn-Mittelwerte zwischen den Firmen verwenden können.
Überprüfen wir nun, ob die Schätzungen dieses Modells wirklich mit den Gruppenmittelwerten übereinstimmen:
# "no-pooling" Mittelwerte aus no.pooling2 extrahieren
np_means <- as.numeric(coef(no.pooling2))
# nicht benötigte Attribute entfernen
emp_means <- as.numeric(unlist(emp_means))
# Äquivalenz überprüfen
all.equal(np_means, emp_means)[1] TRUEZum Schluss plotten wir noch die mit dem “partial pooling” Intercept-Only-Modell geschätzten Mittelwerte und die “no pooling” Mittelwerte des linearen Modells, also die empirischen Firmenmittelwerte:
Code
salary |>
pivot_longer(-diff_means, names_to = "means", values_to = "salary") |>
mutate(means = as.factor(means)) |>
ggplot(aes(x = means, y = salary)) +
geom_boxplot(aes(color = means)) +
geom_point(alpha = 0.6) +
guides(color = "none") +
scale_color_brewer(palette = "Set1") +
theme_classic()
Wir sehen, dass die Verteilung der empirischen Mittelwerte etwas breiter ist als die der geschätzten (“geschrumpften”) Mittelwerte. Im Falle ungleich grosser Unternehmensstichproben wäre die Shrinkage/Schrumpfung noch ausgeprägter, wobei die Mittelwerte von Firmen mit kleineren Stichproben stärker zum Gesamtmittelwert “gezogen” werden würden als die Mittelwerte von Firmen mit grossen Stichproben (was die geringere Genauigkeit der Schätzungen aus kleinen Stichproben widerspiegelt).
1.4 Random-Intercept-Modell (Modell 2)
Dieses Modell enthält einen Level-1-Prädiktor (exp_centered), der jedoch als fester Effekt konzeptualisiert wird (kein Random Slope, nur Random Intercept). Dieses Modell wird insbesondere benötigt, um den Anteil der durch den Level-1-Prädiktor erklärten Level-1-Varianz zu ermitteln (vgl. Eid et al., 2017).
Level-1-Modell:
\(\boldsymbol {y_{mi}=\beta_{0i} + \beta_{1i} \cdot x_{mi} + \varepsilon_{mi}}\)
Level-2-Modell:
\(\boldsymbol {\beta_{0i}=\gamma_{00} + \upsilon_{0i}}\)
\(\boldsymbol {\beta_{1i}=\gamma_{10}}\)
Gesamtmodell:
\(\boldsymbol {y_{mi}=\gamma_{00} + \gamma_{10} \cdot x_{mi} + \upsilon_{0i}+\varepsilon_{mi}}\)
1.4.1 Modell berechnen
# Fitten und Abspeichern des Modells
# Wenn eine Prädiktorvariable im Modell ist,
# muss der Intercept (also 1) nicht zusätzlich angegeben werden.
random.intercept.model <- lmer(salary ~ exp_centered + (1 | company),
data = df, REML = TRUE
)
# Abspeichern von Prädiktionen, die dieses Modell macht.
# Wir speichern diese Prädiktionen (vorhergesagten Werte),
# um das Modell später mit "ggplot2" zu veranschaulichen.
df$random.intercept.preds <- predict(random.intercept.model)
# Output anschauen
summary(random.intercept.model)Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: salary ~ exp_centered + (1 | company)
Data: df
REML criterion at convergence: 1871.8
Scaled residuals:
Min 1Q Median 3Q Max
-2.8261 -0.6843 -0.0048 0.5968 3.9117
Random effects:
Groups Name Variance Std.Dev.
company (Intercept) 0.8769 0.9364
Residual 1.1845 1.0884
Number of obs: 600, groups: company, 20
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 8.73760 0.21406 19.00000 40.82 <2e-16 ***
exp_centered 0.53188 0.02735 579.00000 19.45 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
exp_centerd 0.000 Die Ergebnisse zeigen, dass der Fixed-Effect von exp_centered positiv signifikant ist \((\hat\gamma_{10} = 0.532, p < 0.001)\). Im Durchschnitt aller Firmen steigt das vorhergesagte Einkommen (salary) also mit jedem Jahr Arbeitserfahrung um ca. 0.532 Einheiten (532 CHF) an.
1.4.2 Varianzerklärung durch Level-1-Prädiktor
Wieviel Level-1-Varianz wurde durch exp_centered erklärt?
\(R^2_{Level-1} = \frac {\hat\sigma^2_{\varepsilon1} - \hat\sigma^2_{\varepsilon2}}{\hat\sigma^2_{\varepsilon1}} = \frac {{1.9547}-{1.1845}}{1.9547} = {0.394}\)
39.4 % der Lohnunterschiede innerhalb der Firmen lassen sich durch Unterschiede in der Länge der Arbeitserfahrung zwischen den Mitarbeitenden einer Firma erklären (insgesamt, d.h. im Schnitt über alle Firmen).
\(~\)
Code
df$random.intercept.preds <- predict(random.intercept.model)
ggplot(data = df, aes(
x = exp_centered,
y = random.intercept.preds,
colour = company
)) +
geom_smooth(method = "lm", fullrange = TRUE, se = F, size = .3) +
geom_jitter(aes(y = salary), alpha = .2) +
labs(x = xlabel, y = ylabel) +
ggtitle("Random-Intercept-Modell") +
geom_abline(
intercept = fixef(random.intercept.model)["(Intercept)"],
slope = fixef(random.intercept.model)["exp_centered"]
) +
scale_colour_discrete() +
ggthemes::theme_tufte()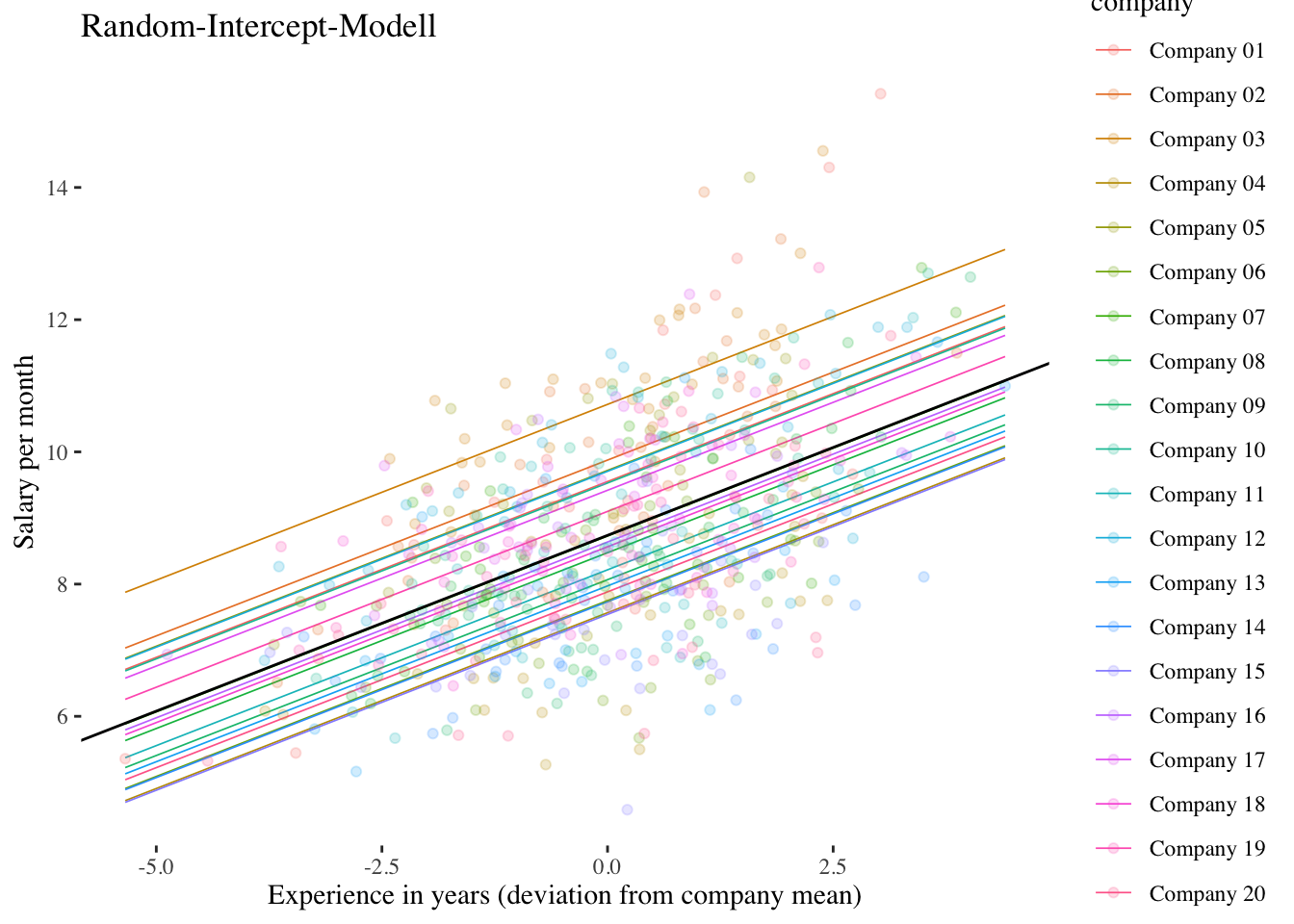
1.5 Random-Coefficients-Modell (Modell 3)
Dieses Modell enthält sowohl einen Random-Intercept, als auch einen Random-Slope. Mit Hilfe dieses Modells kann die Varianz des Level-1-Slopes geschätzt werden. Damit erhalten wir ein Mass für die Unterschiedlichkeit des Effekts (Slope) des Level-1-Prädiktors (X, exp_centered) auf die AV (Y, salary) zwischen den Level-2-Einheiten (company).
Level-1-Modell:
\(\boldsymbol {y_{mi}=\beta_{0i} + \beta_{1i} \cdot x_{mi} + \varepsilon_{mi}}\)
Level-2-Modell:
\(\boldsymbol {\beta_{0i}=\gamma_{00} + \upsilon_{0i}}\)
\(\boldsymbol {\beta_{1i}=\gamma_{10} + \upsilon_{1i}}\)
Gesamtmodell:
\(\boldsymbol {y_{mi}=\gamma_{00} + \gamma_{10} \cdot x_{mi} + \upsilon_{0i} + \upsilon_{1i} \cdot x_{mi} + \varepsilon_{mi}}\)
1.5.1 Modell berechnen
# Fitten und Abspeichern des Modells.
# Wenn für eine Prädiktorvariable ein Random-Slope im Modell ist, muss der
# Intercept (also 1) nicht mehr zusätzlich im Klammerausdruck für die zufälligen
# Effekte angegeben werden.
random.coefficients.model <- lmer(salary ~ exp_centered + (exp_centered | company),
data = df, REML = TRUE
)
# Abspeichern von Prädiktionen, die dieses Modell macht.
# Wir speichern diese Prädiktionen, um das Modell später mit ggplot2
# zu veranschaulichen.
df$random.coefficients.preds <- predict(random.coefficients.model)
# Output anschauen
summary(random.coefficients.model)Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: salary ~ exp_centered + (exp_centered | company)
Data: df
REML criterion at convergence: 1857.5
Scaled residuals:
Min 1Q Median 3Q Max
-2.8740 -0.6582 -0.0030 0.5957 3.3642
Random effects:
Groups Name Variance Std.Dev. Corr
company (Intercept) 0.8785 0.9373
exp_centered 0.0184 0.1357 0.71
Residual 1.1366 1.0661
Number of obs: 600, groups: company, 20
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 8.73760 0.21405 19.00180 40.82 < 2e-16 ***
exp_centered 0.53050 0.04065 19.29006 13.05 5.03e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr)
exp_centerd 0.517 Die Ergebnisse zeigen, dass der Fixed-Effect von exp_centered wiederum positiv signifikant ist \((\hat\gamma_{10} = 0.531, p < 0.001)\) (leicht unterschiedlich im Vergleich zum Random-Intercept-Modell). Das Hauptinteresse im Random-Coefficients-Modell gilt aber der Varianz bzw. Standardabweichung des Random-Slope: \(\hat\sigma^2_{\upsilon_1} = 0.0184\) und damit \(\hat\sigma_{\upsilon_1} = \sqrt{0.0184} = 0.1357\). Die durchschnittliche Abweichung (Level-2-Residuum \(\upsilon_{1i}\)) des exp_centered-Effekts einer Firma vom mittleren Effekt \(\hat\gamma_{10}\) beträgt also 0.1357 Einheiten (135.7 CHF).
Mit der Funktion ranef() kann man sich wieder die einzelnen Random-Effects (jetzt Level-2-Residuen des Intercepts \(\upsilon_{0i}\) und des Slopes \(\upsilon_{1i}\)) ausgeben lassen:
ranef(random.coefficients.model)$company
(Intercept) exp_centered
Company 01 0.86293890 0.206681883
Company 02 1.15821543 0.162568896
Company 03 1.97985927 0.191185325
Company 04 -1.16452562 -0.098713123
Company 05 0.98756095 0.109771623
Company 06 -1.01080913 -0.155736947
Company 07 -0.01614998 -0.015646020
Company 08 -0.23431245 0.046670787
Company 09 -0.63383725 0.029503045
Company 10 0.79781128 0.093373856
Company 11 -0.49876825 0.007304942
Company 12 0.93628430 0.011592283
Company 13 -0.75506236 -0.048869511
Company 14 -1.01724817 -0.130249033
Company 15 -1.21946175 -0.176459297
Company 16 -0.14051872 -0.112235961
Company 17 0.66501590 0.023447960
Company 18 -0.20183736 -0.090510082
Company 19 0.35133550 0.008528235
Company 20 -0.84649052 -0.062208861
with conditional variances for "company" Im Output befindet sich auch eine Angabe zum dritten Random-Effects-Parameter, der in diesem Modell geschätzt wurde, nämlich zur Kovarianz \(\hat\sigma_{\upsilon_0\upsilon_1}\) zwischen den Level-2-Residuen des Intercepts und den Level-2-Residuen des Slopes. Allerdings wird nicht die Kovarianz selbst ausgegeben, sondern ihre standardisierte Variante, die Korrelation \(r_{\upsilon_0\upsilon_1} = 0.71\). Diese besagt, dass der durchschnittliche Lohn eines Mitarbeitenden mit durchschnittlicher Erfahrung in einer Firma (vorhergesagter Wert von salary an der Stelle exp_centered = 0) positiv mit der Steigung von exp_centered korreliert ist. Ein höherer Lohn für durchschnittlich erfahrene Mitarbeitende in einer Firma scheint also mit einem stärkeren Effekt von Erfahrung auf den Lohn in dieser Firma einherzugehen.
1.5.2 Signifikanztest für \(\sigma^2_{\upsilon_1}\): Modellvergleich mit Random-Intercept-Modell
Wenn wir dieses Modell mittels LR-Test mit dem Random-Intercept-Modell (s.o.) vergleichen, werden zwei Parameter gleichzeitig getestet: die Level-2-Varianz des Slopes (\(\sigma^2_{\upsilon_1}\)) und die Level-2-Kovarianz zwischen Intercept und Slope (\(\sigma_{\upsilon_0\upsilon_1}\)). Laut gegenwärtigem Forschungsstand ist dies die beste Methode, um zu überprüfen, ob es eine signifikante Slope-Varianz gibt (vgl. Eid et al., 2017).
1.5.2.1 Modellvergleich von Hand
Zunächst benötigen wir die -2-Log-Likelihoods (Devianzen) der beiden zu vergleichenden Modelle. Diese wird im Modelloutput des jeweiligen Modells unter der Bezeichnung “REML criterion at convergence” ausgegeben.
Wir folgen hier ausserdem den Bezeichnungen für uneingeschränkte Modelle \((M_u)\) und für eingeschränkte (restringierte) Modelle \((M_e)\), wie wir sie auch für die Modellvergleiche bei der logistischen Regression in Statistik III verwendet haben. \(M_u\) steht hier für das Random-Coefficients-Modell, das die zu testenden Parameter (Slope-Varianz \(\sigma^2_{\upsilon_1}\) und Intercept-Slope-Kovarianz \(\sigma_{\upsilon_0\upsilon_1}\)) enthält, \(M_e\) für das Random-Intercept-Model, das genau diese Parameter nicht enthält.
-2-Log-Likelihood random.intercept.model (\(M_e\)): \(-2\cdot ln(L_e) = 1871.8\)
-2-Log-Likelihood random.coefficients.model (\(M_u\)): \(-2\cdot ln(L_u) = 1857.5\)
Berechnen des Modellvergleichstests \(LR(M_u - M_e)\)
\(\chi^2_{emp} = [-2 \cdot ln(L_e)] - [-2 \cdot ln(L_u)] = 1871.8 - 1857.5 = 14.3\)
Anzahl Parameter \((nPar) \space M_u: \space \textbf{6} \space \space (\gamma_{00},\space\gamma_{10},\space\sigma^2_{\varepsilon}, \space\sigma^2_{\upsilon_0}, \space\sigma^2_{\upsilon_1}, \space\sigma_{\upsilon_0\upsilon_1})\)
Anzahl Parameter \((nPar) \space M_e:\space \textbf{4} \space \space (\gamma_{00}, \space\gamma_{10}, \space\sigma^2_{\varepsilon}, \space\sigma^2_{\upsilon_0})\)
\(LR(M_u - M_e)\) ist \(\chi^2\)-verteilt mit \(df = nPar(M_u) - nPar(M_e) = 6 - 4 = 2\)
Kritischer Wert: \(\chi^2_{(0.95, df = 2)} = 5.9915\)
\(~\)
Aber: Es handelt sich genau genommen um eine Mischverteilung aus \(\chi^2_{df=1}\) und \(\chi^2_{df=2}\), da einer der beiden getesteten Parameter \((\sigma^2_{\upsilon_1})\) einen bounded parameter space aufweist (kann nicht kleiner als 0 werden). Daher ist der korrekte kritische Chi-Quadrat-Wert hier das 95 %-Quantil dieser Mischverteilung und liegt bei (gerundet) 5.14 (vgl. Eid et al., 2017).
Der Test ist signifikant, da \(\chi^2_{emp} \space(=14.3) > \chi^2_{krit} \space(=5.14)\).
Beide Parameter zusammen unterscheiden sich also signifikant von 0. Der Fokus der Interpretation liegt hier aber auf dem Parameter der Slope-Varianz \(\sigma^2_{\upsilon_1}\) (nur wenn dieser > 0 ist, kann auch die Intercept-Slope-Kovarianz \(\sigma_{\upsilon_0\upsilon_1}\) überhaupt ungleich 0 sein).
Inhaltlich bedeutet dies, dass sich die Stärke des Effekts von exp_centered auf salary signifikant zwischen den Firmen (company) unterscheidet. Die oben im Random-Coefficients-Modell geschätzte Slope-Varianz von exp_centered \((\hat \sigma^2_{\upsilon_1} = 0.0184)\) ist damit als signifikant zu bewerten.
1.5.2.2 Modellvergleich in R
Wie beim Signifikanztest der Random-Intercept-Varianz \(\sigma^2_{\upsilon_0}\) im Intercept-Only-Modell können wir den Modellvergleich hier wieder mit ranova() vornehmen. Wie oben wird ranova() auf das uneingeschränkte Modell angewandt, die Angabe eines (eingeschränkten) Vergleichsmodells ist nicht notwendig.
ranova(random.coefficients.model)ANOVA-like table for random-effects: Single term deletions
Model:
salary ~ exp_centered + (exp_centered | company)
npar logLik AIC LRT Df
<none> 6 -928.75 1869.5
exp_centered in (exp_centered | company) 4 -935.91 1879.8 14.316 2
Pr(>Chisq)
<none>
exp_centered in (exp_centered | company) 0.0007788 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1\(~\)
Alternativ können wir den Modellvergleich auch mit der uns bereits bekannten Funktion anova() durchführen, indem wir die beiden zu vergleichenden Modelle explizit angeben:
anova(random.coefficients.model, random.intercept.model, refit = FALSE)Data: df
Models:
random.intercept.model: salary ~ exp_centered + (1 | company)
random.coefficients.model: salary ~ exp_centered + (exp_centered | company)
npar AIC BIC logLik deviance Chisq Df
random.intercept.model 4 1879.8 1897.4 -935.91 1871.8
random.coefficients.model 6 1869.5 1895.9 -928.75 1857.5 14.316 2
Pr(>Chisq)
random.intercept.model
random.coefficients.model 0.0007788 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Das Ergebnis zeigt einen signifikanten LR-Test mit \(\chi^2_{emp} = 14.316\). Der (Rundungs-)Unterschied zum Modellvergleich von Hand ergibt sich wegen der ungenaueren Angabe der Devianzen in den Modelloutputs.
Der angegebene \(p\)-Wert ist allerdings noch nicht ganz korrekt, da einer der beiden Parameter - \(\sigma^2_{\upsilon_1}\) - wie oben bereits festgestellt einen bounded parameter space aufweist. Der korrekte \(p\)-Wert auf Basis der Mischverteilung ist daher noch etwas kleiner als der ausgegebene.
\(~\)
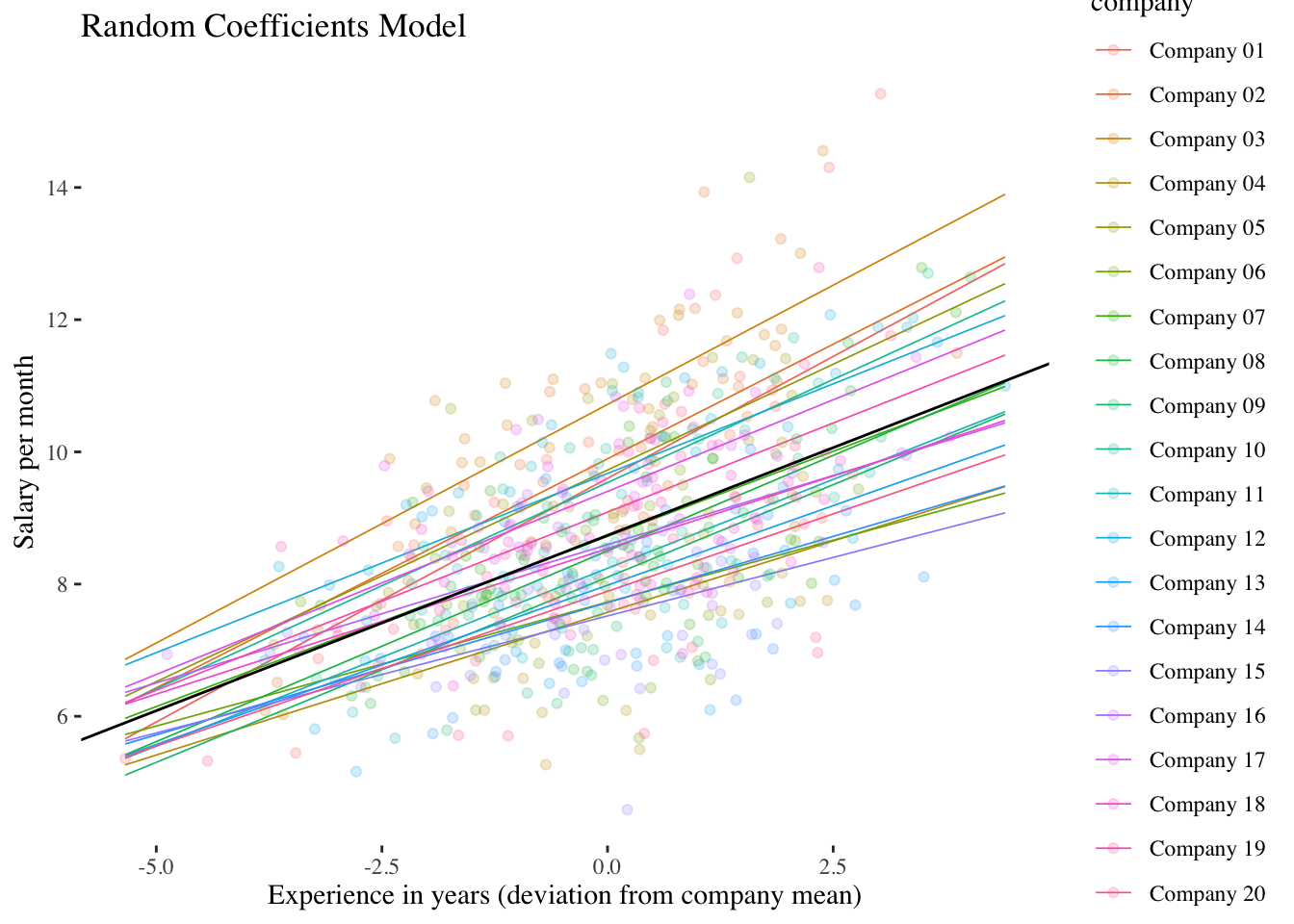
Code
# sal.visualisation$random.intercept.random.slope.plot
df$random.coefficients.preds <- predict(random.coefficients.model)
ggplot(data = df, aes(x = exp_centered, y = random.coefficients.preds, colour = company)) +
geom_smooth(method = "lm", fullrange = TRUE, se = F, size = .3) +
labs(x = xlabel, y = ylabel) +
geom_jitter(aes(y = salary), alpha = .2) +
geom_abline(
intercept = fixef(random.coefficients.model)["(Intercept)"],
slope = fixef(random.coefficients.model)["exp_centered"]
) +
ggtitle("Random Coefficients Model") +
scale_colour_discrete() +
ggthemes::theme_tufte()
1.6 Literatur
Eid, M., Gollwitzer, M., & Schmitt, M. (2017). Statistik und Forschungsmethoden: mit Online-Materialien (5., korrigierte Auflage). Beltz.
Gelman, A., & Hill, J. (2007). Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.