7 Descriptive Statistics
7.1 Summary statistics of all variables in a dataset
The function summary(data_frame) returns descriptive statistics for all variables in a dataset. For numeric variables, the minimum, maximum, quartiles, median, and mean values are returned, for factors the frequencies of the factor levels. In addition, the number of missing values for both variable types is displayed.
We first import our sample data set and assign the variables their scale level (i.e., defining factors as factors). Afterwards, we delete all single items from the data set since they are not needed now. This reduced data set, which we call westost_scales, is then saved as an .Rdata file in our data folder, so that we can load it next time without having to do all the import work again.
library(tidyverse)
library(haven)
westost <- read_sav("data/Beispieldatensatz.sav")
westost$ID <- as.factor(westost$ID)
westost$westost <- as_factor(westost$westost)
westost$geschlecht <- as_factor(westost$geschlecht)
westost$SES <- as_factor(westost$SES, ordered = TRUE)
westost$Deutsch <- as_factor(westost$Deutsch, ordered = TRUE)
westost$Mathe <- as_factor(westost$Mathe, ordered = TRUE)
westost$Fremdspr <- as_factor(westost$Fremdspr, ordered = TRUE)
westost$bildung_vater <- as_factor(westost$bildung_vater)
westost$bildung_mutter <- as_factor(westost$bildung_mutter)
westost$bildung_vater_b <- as_factor(westost$bildung_vater_b)
westost$bildung_mutter_b <- as_factor(westost$bildung_mutter_b)
save(westost, file = "data/westost.Rdata")
westost_scales <- westost %>% select (-c(T1_1:T7_12))
save(westost_scales, file = "data/westost_scales.Rdata")
load(file = "data/westost_scales.Rdata")
westost_scales
#> # A tibble: 286 x 33
#> ID westost geschlecht alter SES Deutsch Mathe Fremdspr Schnitt
#> <fct> <fct> <fct> <dbl> <ord> <ord> <ord> <ord> <dbl>
#> 1 2 West männlich 14 unte… befrie… befr… ausreic… 4
#> 2 14 West männlich 14 durc… befrie… befr… ausreic… 4
#> 3 15 West männlich 14 durc… befrie… befr… befried… 4
#> 4 17 West männlich 15 durc… befrie… befr… ausreic… 4
#> 5 18 West männlich 14 durc… gut gut befried… 4
#> 6 19 West männlich 15 über… befrie… befr… ausreic… 4
#> # … with 280 more rows, and 24 more variables: bildung_vater <fct>,
#> # bildung_mutter <fct>, bildung_vater_b <fct>, bildung_mutter_b <fct>,
#> # swk_akad <dbl>, swk_selbstreg <dbl>, swk_durch <dbl>,
#> # swk_motselbst <dbl>, swk_sozharm <dbl>, swk_bez <dbl>,
#> # unt_eltern <dbl>, unt_freunde <dbl>, sch_leistung <dbl>,
#> # sch_bez <dbl>, sch_regeln <dbl>, ges_gerecht <dbl>, ges_nepot <dbl>,
#> # leben_selbst <dbl>, leben_fam <dbl>, leben_schule <dbl>,
#> # leben_freunde <dbl>, leben_gesamt <dbl>, stress_somat <dbl>,
#> # stress_psych <dbl>With summary() we now can get a descriptive overview of the dataset:
summary(westost_scales)
#> ID westost geschlecht alter
#> 1 : 1 West:143 männlich:152 Min. :13.0
#> 2 : 1 Ost :143 weiblich:134 1st Qu.:14.0
#> 10 : 1 Median :15.0
#> 11 : 1 Mean :14.7
#> 12 : 1 3rd Qu.:15.0
#> 14 : 1 Max. :17.0
#> (Other):280
#> SES Deutsch Mathe
#> sehr niedrig : 1 ungenügend : 0 ungenügend : 0
#> unterdurchschnittlich: 4 mangelhaft : 3 mangelhaft : 11
#> durchschnittlich :186 ausreichend : 52 ausreichend : 55
#> überdurchschnittlich : 69 befriedigend:112 befriedigend:111
#> sehr hoch : 24 gut :100 gut : 88
#> NA's : 2 sehr gut : 16 sehr gut : 19
#> NA's : 3 NA's : 2
#> Fremdspr Schnitt
#> ungenügend : 0 Min. :3.000
#> mangelhaft : 10 1st Qu.:4.000
#> ausreichend : 39 Median :4.500
#> befriedigend:103 Mean :4.462
#> gut :102 3rd Qu.:5.000
#> sehr gut : 21 Max. :6.000
#> NA's : 11 NA's :6
#> bildung_vater
#> Hauptschulabschluss oder niedriger :41
#> Realschulabschluss (mittlere Reife) :94
#> Fachabitur, Abitur :41
#> Fachhochschulabschluss, Universitätsabschluss:93
#> NA's :17
#>
#>
#> bildung_mutter bildung_vater_b
#> Hauptschulabschluss oder niedriger :43 niedrig:135
#> Realschulabschluss (mittlere Reife) :95 hoch :134
#> Fachabitur, Abitur :50 NA's : 17
#> Fachhochschulabschluss, Universitätsabschluss:84
#> NA's :14
#>
#>
#> bildung_mutter_b swk_akad swk_selbstreg swk_durch
#> niedrig:138 Min. :2.429 Min. :2.875 Min. :1.000
#> hoch :134 1st Qu.:4.571 1st Qu.:4.750 1st Qu.:4.667
#> NA's : 14 Median :5.143 Median :5.250 Median :5.333
#> Mean :5.098 Mean :5.246 Mean :5.285
#> 3rd Qu.:5.571 3rd Qu.:5.875 3rd Qu.:6.000
#> Max. :7.000 Max. :7.000 Max. :7.000
#> NA's :1
#> swk_motselbst swk_sozharm swk_bez unt_eltern
#> Min. :3.200 Min. :1.571 Min. :3.333 Min. :1.500
#> 1st Qu.:5.000 1st Qu.:4.857 1st Qu.:5.167 1st Qu.:5.333
#> Median :5.400 Median :5.381 Median :5.667 Median :6.167
#> Mean :5.447 Mean :5.280 Mean :5.616 Mean :5.872
#> 3rd Qu.:6.000 3rd Qu.:5.857 3rd Qu.:6.167 3rd Qu.:6.667
#> Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
#> NA's :1
#> unt_freunde sch_leistung sch_bez sch_regeln
#> Min. :2.000 Min. :1.667 Min. :1.000 Min. :1.750
#> 1st Qu.:5.500 1st Qu.:3.667 1st Qu.:3.163 1st Qu.:4.000
#> Median :6.000 Median :4.333 Median :3.750 Median :4.925
#> Mean :5.928 Mean :4.326 Mean :3.820 Mean :4.875
#> 3rd Qu.:6.667 3rd Qu.:5.000 3rd Qu.:4.500 3rd Qu.:5.750
#> Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
#> NA's :1 NA's :2
#> ges_gerecht ges_nepot leben_selbst leben_fam
#> Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
#> 1st Qu.:3.500 1st Qu.:3.600 1st Qu.:5.000 1st Qu.:5.333
#> Median :4.167 Median :4.400 Median :5.500 Median :6.000
#> Mean :4.160 Mean :4.423 Mean :5.433 Mean :5.760
#> 3rd Qu.:5.000 3rd Qu.:5.200 3rd Qu.:6.000 3rd Qu.:6.667
#> Max. :6.667 Max. :7.000 Max. :7.000 Max. :7.000
#> NA's :3 NA's :1 NA's :2
#> leben_schule leben_freunde leben_gesamt stress_somat
#> Min. :1.333 Min. :2.000 Min. :2.909 Min. :1.000
#> 1st Qu.:4.000 1st Qu.:5.500 1st Qu.:5.000 1st Qu.:2.167
#> Median :4.667 Median :6.000 Median :5.455 Median :3.000
#> Mean :4.670 Mean :5.898 Mean :5.417 Mean :3.020
#> 3rd Qu.:5.333 3rd Qu.:6.500 3rd Qu.:5.909 3rd Qu.:3.667
#> Max. :7.000 Max. :7.000 Max. :6.909 Max. :7.000
#> NA's :1 NA's :1 NA's :1 NA's :3
#> stress_psych
#> Min. :1.000
#> 1st Qu.:2.167
#> Median :2.917
#> Mean :2.989
#> 3rd Qu.:3.667
#> Max. :6.833
#> NA's :27.2 Descriptive statistics for nominal variables
7.2.1 Frequencies with table()
Using table() we can display the frequencies of the categories (factor levels) of a factor. This is particularly useful if we are interested in the combined frequencies of several factors as in a cross-tabulation.
table(westost_scales$bildung_vater)
#>
#> Hauptschulabschluss oder niedriger
#> 41
#> Realschulabschluss (mittlere Reife)
#> 94
#> Fachabitur, Abitur
#> 41
#> Fachhochschulabschluss, Universitätsabschluss
#> 93
table(westost_scales$bildung_vater_b, westost_scales$bildung_mutter_b)
#>
#> niedrig hoch
#> niedrig 102 32
#> hoch 35 99
table(westost_scales$westost, westost_scales$bildung_mutter)
#>
#> Hauptschulabschluss oder niedriger
#> West 43
#> Ost 0
#>
#> Realschulabschluss (mittlere Reife) Fachabitur, Abitur
#> West 52 20
#> Ost 43 30
#>
#> Fachhochschulabschluss, Universitätsabschluss
#> West 26
#> Ost 58Let’s generate some frequency plots with ggplot2:
p <- westost_scales %>%
select(bildung_vater) %>%
drop_na() %>%
ggplot(aes(x = bildung_vater))
p + geom_bar(fill = "darkblue") +
xlab("Education of the Father") +
ylab("Frequency")
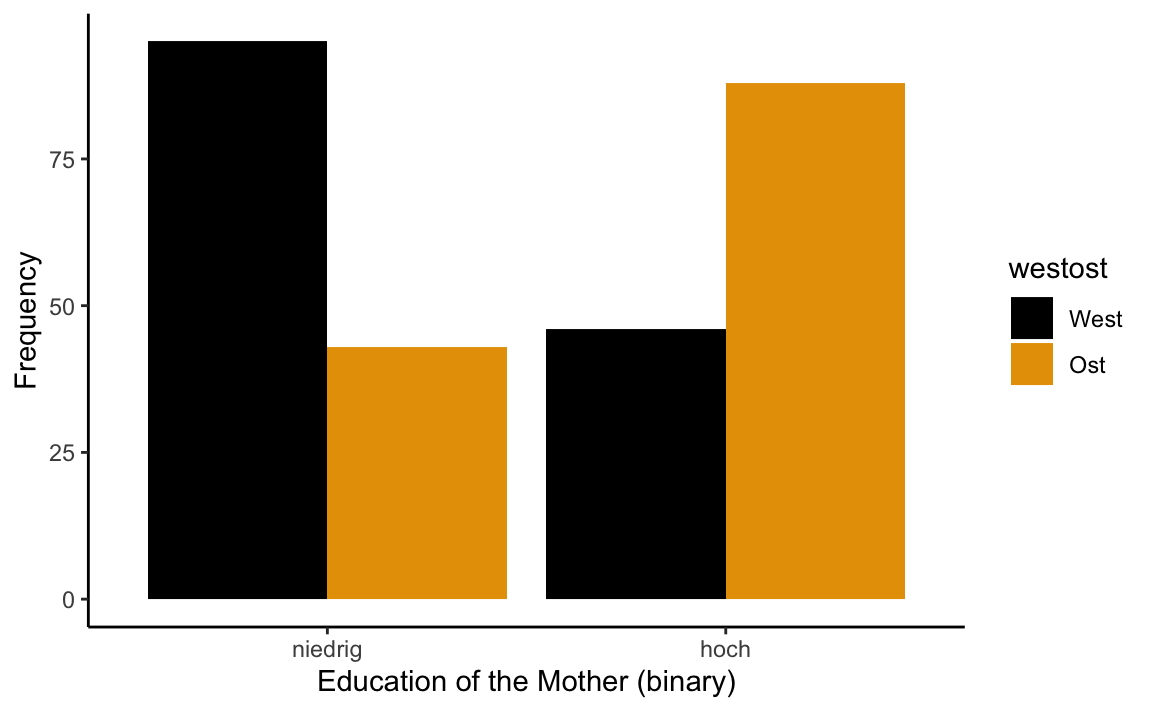
p1 <- westost_scales %>%
select(bildung_mutter_b, westost) %>%
drop_na() %>%
ggplot(aes(x = bildung_mutter_b, fill = westost))
p1 + geom_bar(position = "dodge") +
xlab("Education of the Mother (binary)") +
ylab("Frequency") +
theme_classic() +
scale_fill_manual(values = c("#000000", "#E69F00"))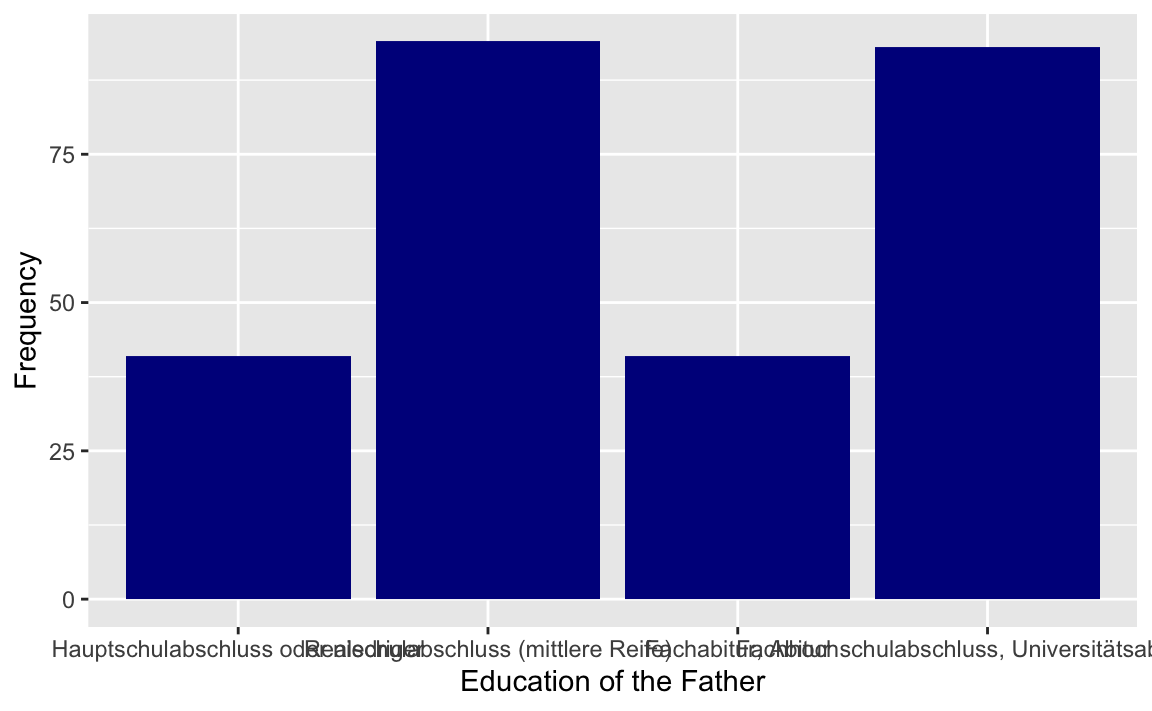
With prop.table() we can get proportions (relative frequencies):
table(westost_scales$bildung_vater_b, westost_scales$bildung_mutter_b) %>% prop.table() %>% round(2)
#>
#> niedrig hoch
#> niedrig 0.38 0.12
#> hoch 0.13 0.37
# or in percentages
100*table(westost_scales$bildung_vater_b, westost_scales$bildung_mutter_b) %>% prop.table() %>% round(4)
#>
#> niedrig hoch
#> niedrig 38.06 11.94
#> hoch 13.06 36.94In most cases we are not interested in the total proportions (which add up to 1 or 100% across the entire table), but in the row-conditional or column-conditional relative frequencies. The former are obtained using margin = 1 in the prop.table() function, the latter with margin = 2. Since there is no further argument, we can also directly specify the value of the argument, i.e. prop.table(1) for row-conditional proportions and prop.table(2) for column-conditional proportions.
table(westost_scales$geschlecht, westost_scales$westost)
#>
#> West Ost
#> männlich 83 69
#> weiblich 60 74
# Relative frequencies (entire table)
table(westost_scales$geschlecht, westost_scales$westost) %>% prop.table() %>% round(2)
#>
#> West Ost
#> männlich 0.29 0.24
#> weiblich 0.21 0.26
# Row-conditional relative frequencies
table(westost_scales$geschlecht, westost_scales$westost) %>% prop.table(1) %>% round(2)
#>
#> West Ost
#> männlich 0.55 0.45
#> weiblich 0.45 0.55
# Column-conditional relative frequencies
table(westost_scales$geschlecht, westost_scales$westost) %>% prop.table(2) %>% round(2)
#>
#> West Ost
#> männlich 0.58 0.48
#> weiblich 0.42 0.527.2.2 Mode
There is no separate function for calculating the mode of a nominal variable. Either you read the mode (the category with the highest frequency) from the frequency table (or the frequency diagram), or you can help yourself with:
names(which.max(table(westost_scales$bildung_vater)))
#> [1] "Realschulabschluss (mittlere Reife)"7.3 Descriptive statistics for ordinal and metric Variables
Most of the functions needed for describing the distributional characteristics of ordinal and metric variables we already know from the earlier chapter on the R language.
mean(x, na.rm = FALSE) Arithmetic mean
sd(x) (Sample) Standard Deviation
var(x) (Sample) Variance
median(x) Median
quantile(x, probs, type) Quantile of x. probs: vector with probabilities
min(x) Minimum value of x
max(x) Maximum value of x
range(x) x_min and x_maxExamples
Let’s create a vector with 16 numbers between 1 and 9 and sort it:
x <- c(4, 7, 9, 2, 3, 6, 6, 4, 1, 2, 8, 5, 5, 7, 3, 2)
n <- length(x)
x <- sort(x)
x
#> [1] 1 2 2 2 3 3 4 4 5 5 6 6 7 7 8 9median(x)
#> [1] 4.5
quantile(x, c(.25, .75))
#> 25% 75%
#> 2.75 6.25The median = 4.5 corresponds to our expectations, as it is the mean of the 8th and 9th sorted values. The quartiles are \(Q_1=2.75\) and \(Q_3=6.25\)`. This is probably not what you’ve learned in your statistics course (at least not with us…). We have learned that if \(n\cdot p\) is not an integer, then the quantile is the \([(n\cdot p) + 1]\)th value of the distribution; on the other hand, if \(n\cdot p\) is an integer, the respective quantile is the mean of the \((n\cdot p)\)th and the \([(n\cdot p) + 1]\)th value. Since 16 can be devided by 4, both \(n\cdot 0.25\) and \(n\cdot 0.75\) are integers. Thus, the first quartile should be \(Q_1=\frac {x_{n \cdot 0.25}+x_{n \cdot 0.25+1}}{2} = \frac {x_4+x_5}{2}= \frac {2+3}{2}= 2.5\) and the third quartile should be \(Q_3=\frac {x_{n \cdot 0.75}+x_{n \cdot 0.75+1}}{2} = \frac {x_{12}+x_{13}}{2}= \frac {6 + 7}{2}= 6.5\). But that’s not what we obtained here…
The short and simple answer to this riddle is that quantile() has nine different methods (type = 1-9) to compute the quantiles of a distribution (help('quantile')). The default method is type = 7, but the method we prefer is type = 2. Therefore:
quantile(x, c(.25, .75), type = 2)
#> 25% 75%
#> 2.5 6.5Which method is used by summary()?
summary(x)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.000 2.750 4.500 4.625 6.250 9.000Surprise! Summary also uses type = 7.
7.3.1 Descriptive summary of selected numerical variables
install.packages("RcmdrMisc")
Descriptive statistics for metric variables can be also obtained by the numSummary() function from the RcmdrMisc package.
The generic form of this function is: numSummary(df[, c("var1", "var2"], groups = df$factor, statistics = c("mean", "sd", "quantiles"), quantiles = c(0,.25,.5,.75,1)).
Additional statistics options are: se(mean) (standard error of the mean = \(\frac {sd}{\sqrt{n}}\)), cv (coefficient of variation = SD/mean), skewness, and kurtosis.
Example: Let us calculate descriptive statistics for the variables “Support by parents” (unt_eltern) and “Support by friends” (unt_friends) with mean value, standard deviation, standard error of the mean, skewness, kurtosis as well as the 10% and 90% quantiles. Using the groups argument we can do this separately for the levels of the factor (geschlecht).
library(RcmdrMisc)
numSummary(westost_scales[,c("unt_eltern", "unt_freunde")],
groups = westost_scales$geschlecht,
statistics = c("mean", "sd", "se(mean)", "skewness",
"kurtosis", "quantiles"),
quantiles = c(.1,.9))
#>
#> Variable: unt_eltern
#> mean sd se(mean) skewness kurtosis 10% 90%
#> männlich 5.94415 0.8687628 0.07069892 -1.204500 1.088983 4.666667 6.833333
#> weiblich 5.79005 1.1232414 0.09703328 -1.332349 2.016779 4.333333 6.833333
#> n NA
#> männlich 151 1
#> weiblich 134 0
#>
#> Variable: unt_freunde
#> mean sd se(mean) skewness kurtosis 10%
#> männlich 5.584868 1.0055152 0.08155806 -0.8628965 0.8376967 4.333333
#> weiblich 6.319549 0.7416894 0.06431263 -2.2457703 8.4513611 5.500000
#> 90% n NA
#> männlich 6.833333 152 0
#> weiblich 7.000000 133 1p1 <- westost_scales %>%
select(unt_eltern, geschlecht) %>%
drop_na() %>%
ggplot(aes(x = unt_eltern, fill = geschlecht, y = ..density..))
p1 + geom_histogram(binwidth = 0.5,
position = "identity",
alpha = 0.5) +
scale_fill_manual(values = c("#000000", "#E69F00")) +
xlab("Support by Parents")
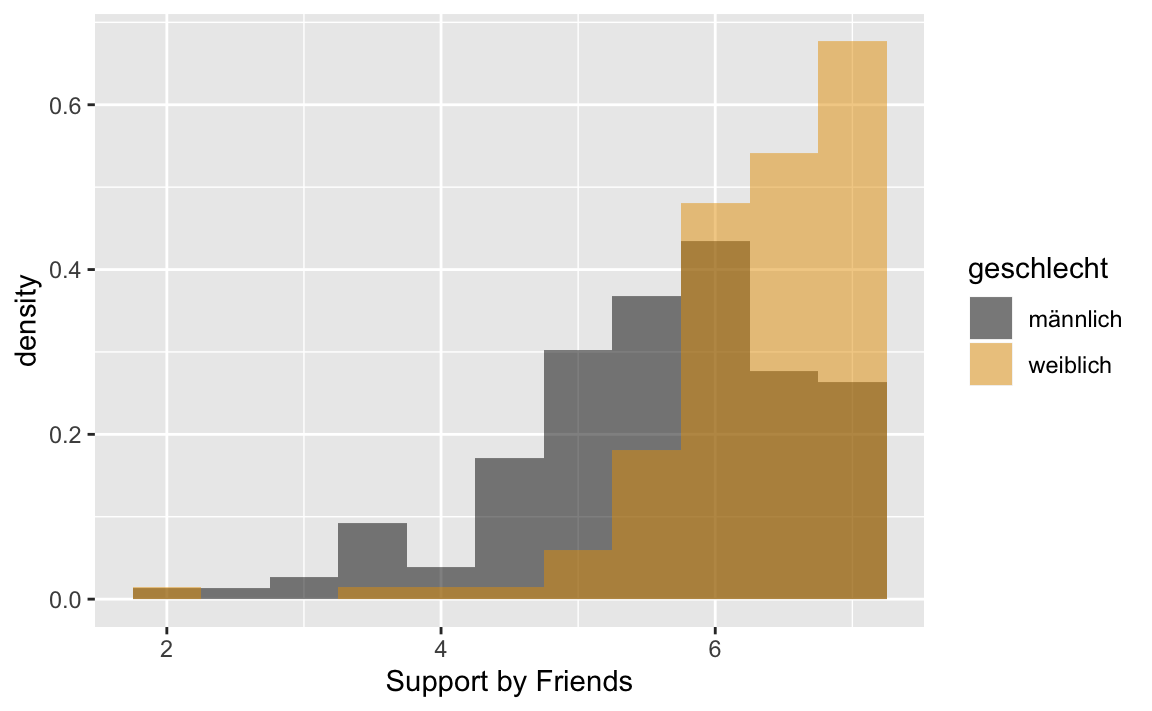
p2 <- westost_scales %>%
select(unt_freunde, geschlecht) %>%
drop_na() %>%
ggplot(aes(x = unt_freunde, fill = geschlecht, y = ..density..))
p2 + geom_histogram(binwidth = 0.5,
position = "identity",
alpha = 0.5) +
scale_fill_manual(values = c("#000000", "#E69F00"))+
xlab("Support by Friends")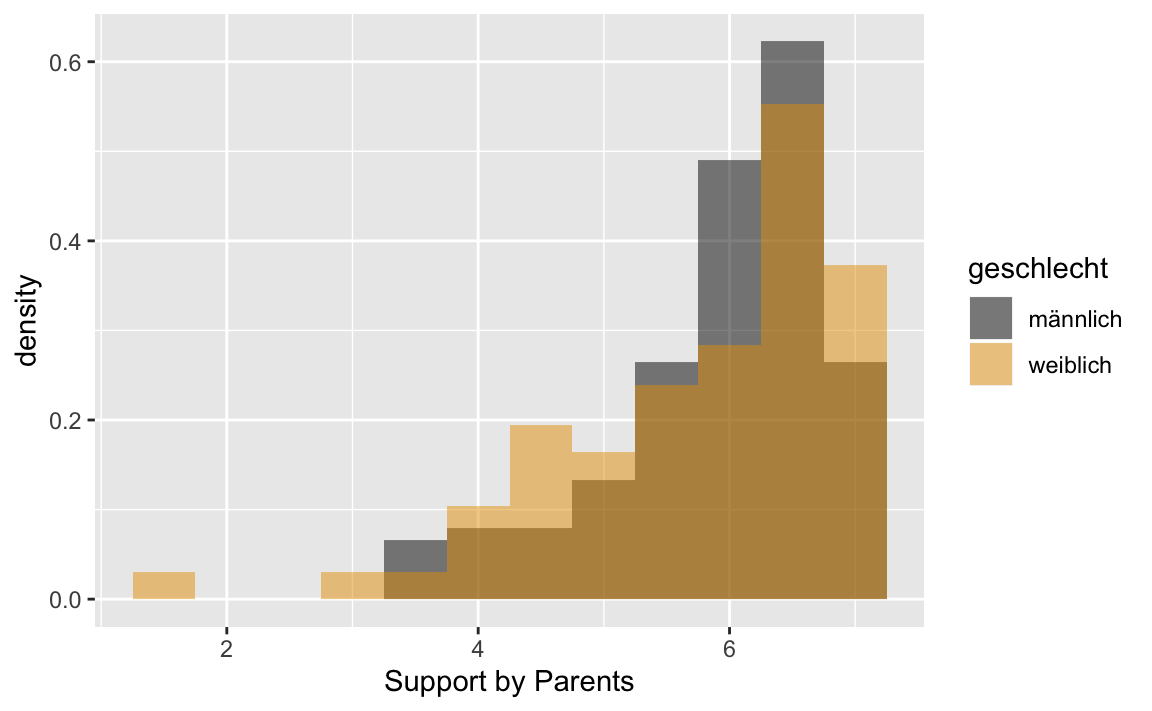
7.3.2 Table with statistics (tapply())
The tapply () function can be used to display selected descriptive statistics for the combined levels of several factors. Useful for the presentation of means in 2-factorial ANOVAS. The generic form is: tapply(df$var1, list(factor1 = df$factor1, factor2 = df$factor2), statistic, na.rm = TRUE).
statistic has to be replaced by the desired statistic (only one at a time), e.g. mean, median, sum, sd.
Let’s display the means of the variable “Support by Parents” for the combined factors geschlecht and westost:
tapply(westost_scales$unt_eltern,
list(Geschlecht = westost_scales$geschlecht, Region = westost_scales$westost),
mean, na.rm = TRUE) %>%
round(2)
#> Region
#> Geschlecht West Ost
#> männlich 5.79 6.13
#> weiblich 5.74 5.83We did the same already using dplyr:
westost_scales %>%
group_by(geschlecht, westost) %>%
summarise(mean = mean(unt_eltern, na.rm = TRUE))
#> # A tibble: 4 x 3
#> # Groups: geschlecht [2]
#> geschlecht westost mean
#> <fct> <fct> <dbl>
#> 1 männlich West 5.79
#> 2 männlich Ost 6.13
#> 3 weiblich West 5.74
#> 4 weiblich Ost 5.83
# Caution: If we use drop_na() to remove missing values, all cases with missings
# anywhere in the dataset will be removed. In this case, it is necessary to define
# a new dataset including only the relevant variables first!
westost_scales %>%
group_by(geschlecht, westost) %>%
drop_na() %>%
summarise(mean = mean(unt_eltern))
#> # A tibble: 4 x 3
#> # Groups: geschlecht [2]
#> geschlecht westost mean
#> <fct> <fct> <dbl>
#> 1 männlich West 5.78
#> 2 männlich Ost 6.12
#> 3 weiblich West 5.71
#> 4 weiblich Ost 5.737.3.3 Descriptive statistics for metric variables using the psych package
install.packages("psych")
The psych package is often used for data analysis in psychology. It has a useful function for descriptive statistics for numerical variables: describe(). The generic form is: describe(x, na.rm = TRUE, interp = FALSE, skew = TRUE, ranges = TRUE, trim = .1, type = 3, check = TRUE).
x stands for the data frame or the variable to be analyzed (df$variable). The defaults are:
* interp = FALSE refers to the definition of the median (interp = TRUE uses our method of averaging adjacent values for an even n) * skew = TRUE displays skewness, kurtosis and the trimmed mean * ranges = TRUE displays the range * trim = .1 refers to the proportion of the distribution that is trimmed at the lower and upper ends for the trimmed mean (default trimming is 10% on both sides, thus the trimmed mean is computed from the middle 80% of the data) * type = 3 refers to the method of computing skewness and kurtosis (more here: ?psych::describe) * check = TRUE refers to checking for non-numeric variables in the dataset (for which describe has no use); if check = FALSE non-numeric variables exist, an error message is displayed.
library(psych)
describe(westost_scales)
#> vars n mean sd median trimmed mad min max
#> ID* 1 286 143.50 82.71 143.50 143.50 106.01 1.00 286.00
#> westost* 2 286 1.50 0.50 1.50 1.50 0.74 1.00 2.00
#> geschlecht* 3 286 1.47 0.50 1.00 1.46 0.00 1.00 2.00
#> alter 4 286 14.70 0.76 15.00 14.65 1.48 13.00 17.00
#> SES* 5 284 3.39 0.68 3.00 3.29 0.00 1.00 5.00
#> Deutsch* 6 283 4.26 0.86 4.00 4.27 1.48 2.00 6.00
#> Mathe* 7 284 4.17 0.95 4.00 4.18 1.48 2.00 6.00
#> Fremdspr* 8 275 4.31 0.93 4.00 4.33 1.48 2.00 6.00
#> Schnitt 9 280 4.46 0.69 4.50 4.51 0.74 3.00 6.00
#> bildung_vater* 10 269 2.69 1.10 2.00 2.74 1.48 1.00 4.00
#> bildung_mutter* 11 272 2.64 1.08 2.00 2.68 1.48 1.00 4.00
#> bildung_vater_b* 12 269 1.50 0.50 1.00 1.50 0.00 1.00 2.00
#> bildung_mutter_b* 13 272 1.49 0.50 1.00 1.49 0.00 1.00 2.00
#> swk_akad 14 286 5.10 0.77 5.14 5.11 0.85 2.43 7.00
#> swk_selbstreg 15 286 5.25 0.81 5.25 5.28 0.93 2.88 7.00
#> swk_durch 16 285 5.28 0.99 5.33 5.35 0.99 1.00 7.00
#> swk_motselbst 17 286 5.45 0.77 5.40 5.48 0.89 3.20 7.00
#> swk_sozharm 18 286 5.28 0.78 5.38 5.30 0.78 1.57 7.00
#> swk_bez 19 286 5.62 0.75 5.67 5.66 0.74 3.33 7.00
#> unt_eltern 20 285 5.87 1.00 6.17 6.01 0.74 1.50 7.00
#> unt_freunde 21 285 5.93 0.96 6.00 6.06 0.99 2.00 7.00
#> sch_leistung 22 284 4.33 1.20 4.33 4.33 0.99 1.67 7.00
#> sch_bez 23 286 3.82 1.12 3.75 3.82 1.00 1.00 7.00
#> sch_regeln 24 286 4.88 1.16 4.93 4.88 1.30 1.75 7.00
#> ges_gerecht 25 286 4.16 1.03 4.17 4.19 0.99 1.00 6.67
#> ges_nepot 26 283 4.42 1.09 4.40 4.43 1.19 1.00 7.00
#> leben_selbst 27 285 5.43 1.10 5.50 5.54 0.74 1.00 7.00
#> leben_fam 28 284 5.76 1.01 6.00 5.88 0.99 1.00 7.00
#> leben_schule 29 285 4.67 1.06 4.67 4.73 0.99 1.33 7.00
#> leben_freunde 30 285 5.90 0.81 6.00 5.95 0.74 2.00 7.00
#> leben_gesamt 31 285 5.42 0.69 5.45 5.46 0.67 2.91 6.91
#> stress_somat 32 283 3.02 1.19 3.00 2.93 0.99 1.00 7.00
#> stress_psych 33 284 2.99 1.20 2.92 2.91 1.11 1.00 6.83
#> range skew kurtosis se
#> ID* 285.00 0.00 -1.21 4.89
#> westost* 1.00 0.00 -2.01 0.03
#> geschlecht* 1.00 0.13 -1.99 0.03
#> alter 4.00 0.36 -0.36 0.04
#> SES* 4.00 0.91 0.73 0.04
#> Deutsch* 4.00 -0.09 -0.50 0.05
#> Mathe* 4.00 -0.15 -0.38 0.06
#> Fremdspr* 4.00 -0.35 -0.15 0.06
#> Schnitt 3.00 -0.41 -0.43 0.04
#> bildung_vater* 3.00 -0.06 -1.41 0.07
#> bildung_mutter* 3.00 -0.01 -1.34 0.07
#> bildung_vater_b* 1.00 0.01 -2.01 0.03
#> bildung_mutter_b* 1.00 0.03 -2.01 0.03
#> swk_akad 4.57 -0.16 0.02 0.05
#> swk_selbstreg 4.12 -0.35 -0.31 0.05
#> swk_durch 6.00 -0.80 1.45 0.06
#> swk_motselbst 3.80 -0.37 -0.32 0.05
#> swk_sozharm 5.43 -0.55 1.18 0.05
#> swk_bez 3.67 -0.48 -0.23 0.04
#> unt_eltern 5.50 -1.35 2.05 0.06
#> unt_freunde 5.00 -1.25 1.85 0.06
#> sch_leistung 5.33 -0.01 -0.37 0.07
#> sch_bez 6.00 -0.04 -0.05 0.07
#> sch_regeln 5.25 -0.10 -0.64 0.07
#> ges_gerecht 5.67 -0.26 -0.27 0.06
#> ges_nepot 6.00 -0.08 -0.10 0.06
#> leben_selbst 6.00 -1.28 2.41 0.07
#> leben_fam 6.00 -1.27 2.27 0.06
#> leben_schule 5.67 -0.48 0.11 0.06
#> leben_freunde 5.00 -1.16 3.10 0.05
#> leben_gesamt 4.00 -0.79 1.14 0.04
#> stress_somat 6.00 0.81 0.99 0.07
#> stress_psych 5.83 0.65 0.42 0.07
describe(westost_scales[, c("unt_eltern", "unt_freunde")])
#> vars n mean sd median trimmed mad min max range skew
#> unt_eltern 1 285 5.87 1.00 6.17 6.01 0.74 1.5 7 5.5 -1.35
#> unt_freunde 2 285 5.93 0.96 6.00 6.06 0.99 2.0 7 5.0 -1.25
#> kurtosis se
#> unt_eltern 2.05 0.06
#> unt_freunde 1.85 0.06
describe(westost_scales[, c("unt_eltern", "unt_freunde")], trim = 0.2)
#> vars n mean sd median trimmed mad min max range skew
#> unt_eltern 1 285 5.87 1.00 6.17 6.08 0.74 1.5 7 5.5 -1.35
#> unt_freunde 2 285 5.93 0.96 6.00 6.09 0.99 2.0 7 5.0 -1.25
#> kurtosis se
#> unt_eltern 2.05 0.06
#> unt_freunde 1.85 0.06
describe(westost_scales[, c("unt_eltern", "unt_freunde")], skew = FALSE,
range = FALSE)
#> vars n mean sd se
#> unt_eltern 1 285 5.87 1.00 0.06
#> unt_freunde 2 285 5.93 0.96 0.06mad stands for median average deviation (mean absolute deviation from the median, an alternative measure of dispersion). The variables recognized as factors are given a * in the table. Nevertheless, their (mostly useless) statistics are displayed in spite of the detection. We are mainly interested in the variables unt_eltern and unt_friends. With trim = 0.2 we request a trimmed mean where 20% of the values at the lower end of the distribution and 20% of the values at the upper end of the distribution are removed. Finally, with skew = FALSE, range = FALSE we request a descriptive statistic without skewness and kurtosis as well as without median, trimmed, mad, min, max, range.
7.4 Descriptive statistics with jmv
The package jmv is the R package for the fabulous new statistics program jamovi. Everything that can be done in jamovi can also be done directly in R. When jamovi is run in syntax mode it is even possible to copy-paste the generated R code directly into an R markdown document like this one.
For the example, let’s first get a dataset swk including all self-efficacy scales + the gender variable:
swk <- westost_scales %>%
select(starts_with("swk"), "geschlecht")
names(swk)
#> [1] "swk_akad" "swk_selbstreg" "swk_durch" "swk_motselbst"
#> [5] "swk_sozharm" "swk_bez" "geschlecht"Descriptive statistics can be obtained with descriptives().
library(jmv)
descriptives(
data = swk,
vars = c(
"swk_akad",
"swk_selbstreg",
"swk_motselbst",
"swk_durch",
"swk_sozharm",
"swk_bez"),
splitBy = "geschlecht")
#>
#> DESCRIPTIVES
#>
#> Descriptives
#> ──────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> geschlecht swk_akad swk_selbstreg swk_motselbst swk_durch swk_sozharm swk_bez
#> ──────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> N männlich 152 152 152 151 152 152
#> weiblich 134 134 134 134 134 134
#> Missing männlich 0 0 0 1 0 0
#> weiblich 0 0 0 0 0 0
#> Mean männlich 5.14 5.16 5.43 5.48 5.30 5.55
#> weiblich 5.05 5.34 5.46 5.06 5.26 5.69
#> Median männlich 5.21 5.25 5.40 5.67 5.29 5.67
#> weiblich 5.14 5.38 5.60 5.33 5.43 5.83
#> Minimum männlich 3.29 2.88 3.20 3.00 3.86 3.33
#> weiblich 2.43 3.43 3.50 1.00 1.57 3.83
#> Maximum männlich 7.00 6.88 7.00 7.00 7.00 7.00
#> weiblich 7.00 7.00 7.00 7.00 6.86 7.00
#> ──────────────────────────────────────────────────────────────────────────────────────────────────────────────With ?jmv::descriptives we get an overview of all the options:
descriptives(data, vars, splitBy = NULL, freq = FALSE, hist = FALSE,
dens = FALSE, bar = FALSE, barCounts = FALSE, box = FALSE,
violin = FALSE, dot = FALSE, dotType = "jitter", n = TRUE,
missing = TRUE, mean = TRUE, median = TRUE, mode = FALSE,
sum = FALSE, sd = FALSE, variance = FALSE, range = FALSE,
min = TRUE, max = TRUE, se = FALSE, skew = FALSE, kurt = FALSE,
quart = FALSE, pcEqGr = FALSE, pcNEqGr = 4)
Arguments
data the data as a data frame
vars a vector of strings naming the variables of interest in data
splitBy a vector of strings naming the variables used to split vars
freq TRUE or FALSE (default), provide frequency tables (nominal, ordinal
variables only)
hist TRUE or FALSE (default), provide histograms (continuous variables only)
dens TRUE or FALSE (default), provide density plots (continuous variables only)
bar TRUE or FALSE (default), provide bar plots (nominal, ordinal variables only)
barCounts TRUE or FALSE (default), add counts to the bar plots
box TRUE or FALSE (default), provide box plots (continuous variables only)
violin TRUE or FALSE (default), provide violin plots (continuous variables only)
dot TRUE or FALSE (default), provide dot plots (continuous variables only)
n TRUE (default) or FALSE, provide the sample size
missing TRUE (default) or FALSE, provide the number of missing values
mean TRUE (default) or FALSE, provide the mean
median TRUE (default) or FALSE, provide the median
mode TRUE or FALSE (default), provide the mode
sum TRUE or FALSE (default), provide the sum
sd TRUE or FALSE (default), provide the standard deviation
variance TRUE or FALSE (default), provide the variance
range TRUE or FALSE (default), provide the range
min TRUE (default) or FALSE, provide the minimum
max TRUE (default) or FALSE, provide the maximum
se TRUE or FALSE (default), provide the standard error
skew TRUE or FALSE (default), provide the skewness
kurt TRUE or FALSE (default), provide the kurtosis
quart TRUE or FALSE (default), provide quartiles
pcEqGr TRUE or FALSE (default), provide quantiles
pcNEqGr an integer (default: 4) specifying the number of equal groupsLet’s try some of these:
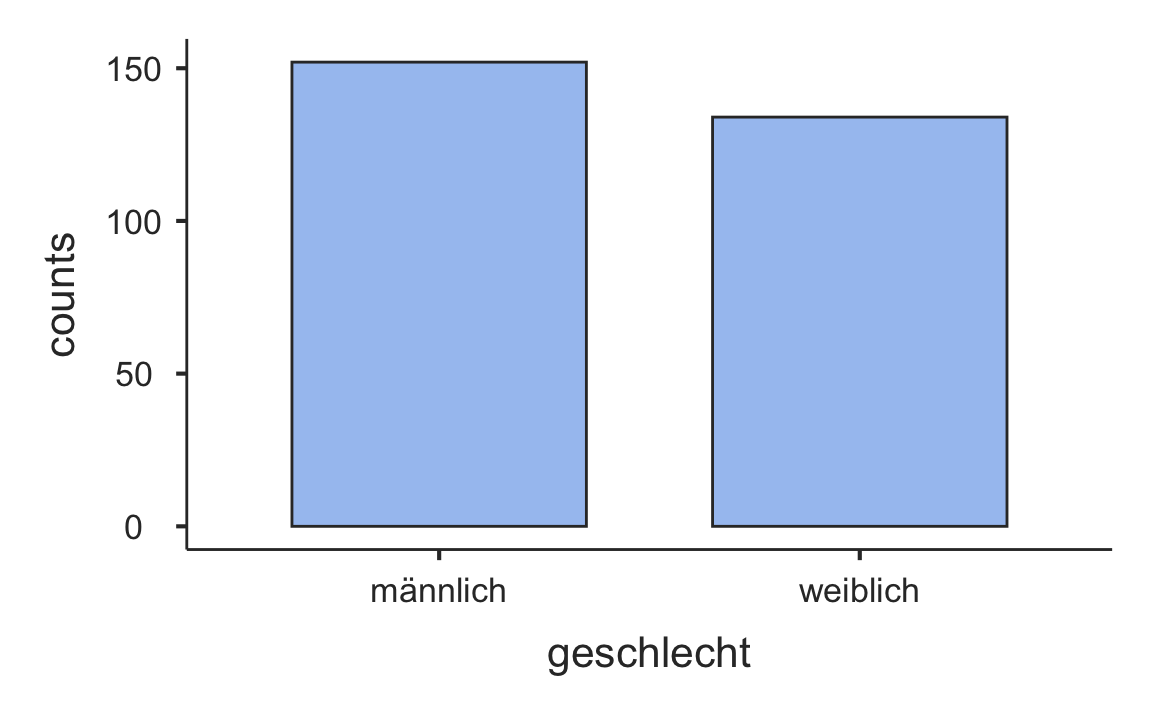
descriptives(
data = swk,
vars = c(
"geschlecht",
"swk_akad",
"swk_selbstreg",
"swk_motselbst"),
freq = TRUE,
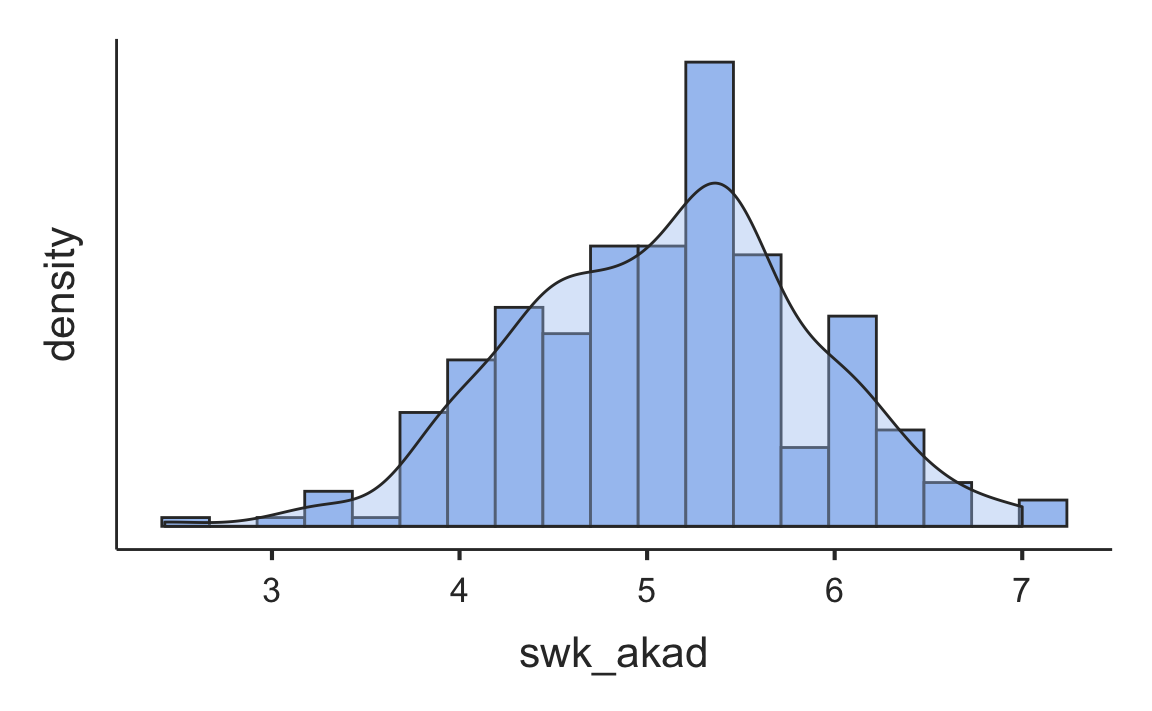
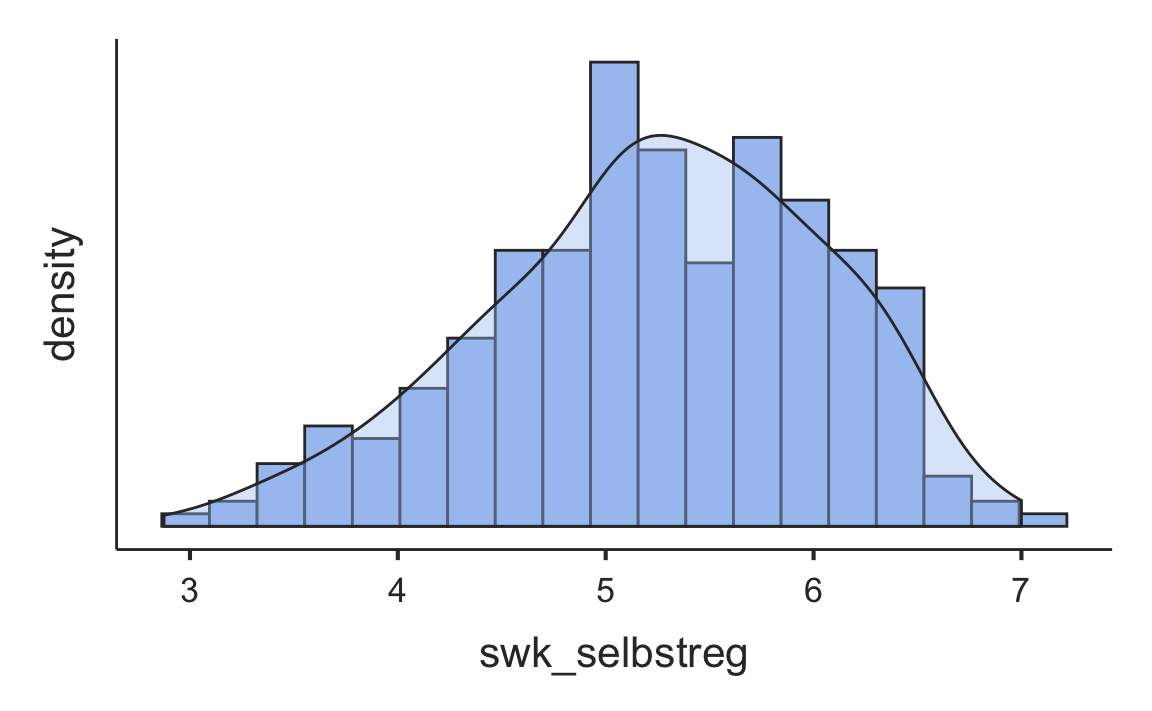
hist = TRUE,
dens = TRUE,
bar = TRUE,
barCounts = TRUE,
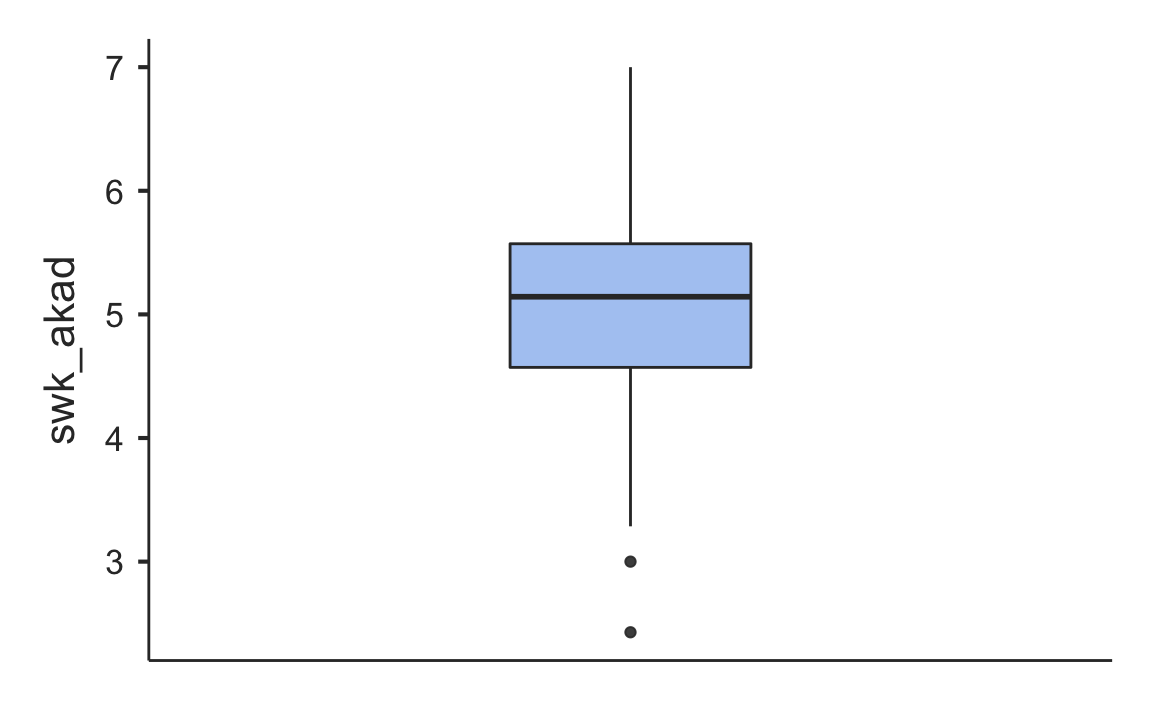
box = TRUE,
sd = TRUE,
variance = TRUE,
range = TRUE,
se = TRUE,
skew = TRUE,
kurt = TRUE,
quart = TRUE,
pcEqGr = TRUE,
pcNEqGr = 10
)
#>
#> DESCRIPTIVES
#>
#> Descriptives
#> ───────────────────────────────────────────────────────────────────────────────────
#> geschlecht swk_akad swk_selbstreg swk_motselbst
#> ───────────────────────────────────────────────────────────────────────────────────
#> N 286 286 286 286
#> Missing 0 0 0 0
#> Mean 5.10 5.25 5.45
#> Std. error mean 0.0455 0.0476 0.0454
#> Median 5.14 5.25 5.40
#> Standard deviation 0.770 0.805 0.768
#> Variance 0.593 0.648 0.590
#> Range 4.57 4.12 3.80
#> Minimum 2.43 2.88 3.20
#> Maximum 7.00 7.00 7.00
#> Skewness -0.161 -0.359 -0.374
#> Std. error skewness 0.144 0.144 0.144
#> Kurtosis 0.0615 -0.279 -0.288
#> Std. error kurtosis 0.287 0.287 0.287
#> 25th percentile 4.57 4.75 5.00
#> 50th percentile 5.14 5.25 5.40
#> 75th percentile 5.57 5.88 6.00
#> 10th percentile 4.14 4.12 4.40
#> 20th percentile 4.43 4.62 4.80
#> 30th percentile 4.66 4.88 5.00
#> 40th percentile 4.86 5.12 5.33
#> 50th percentile 5.14 5.25 5.40
#> 60th percentile 5.33 5.50 5.80
#> 70th percentile 5.43 5.75 6.00
#> 80th percentile 5.71 6.00 6.20
#> 90th percentile 6.07 6.25 6.40
#> ───────────────────────────────────────────────────────────────────────────────────
#>
#>
#> FREQUENCIES
#>
#> Frequencies of geschlecht
#> ────────────────────────────────────────────────────
#> Levels Counts % of Total Cumulative %
#> ────────────────────────────────────────────────────
#> männlich 152 53.1 53.1
#> weiblich 134 46.9 100.0
#> ────────────────────────────────────────────────────
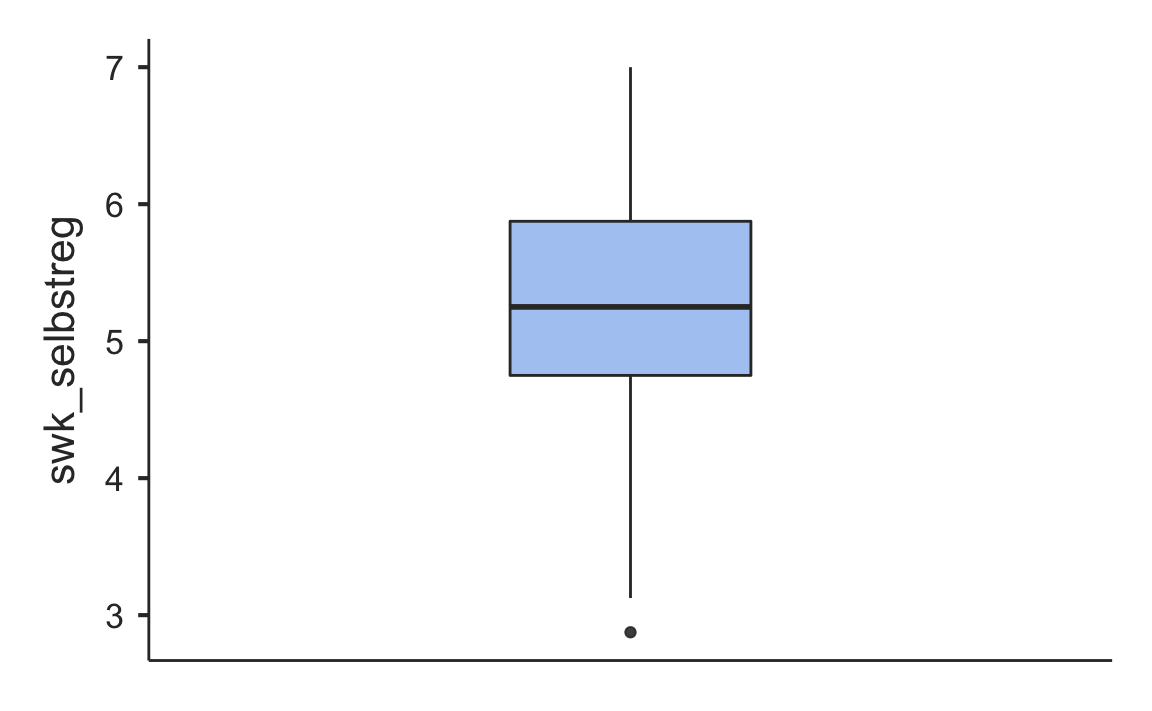
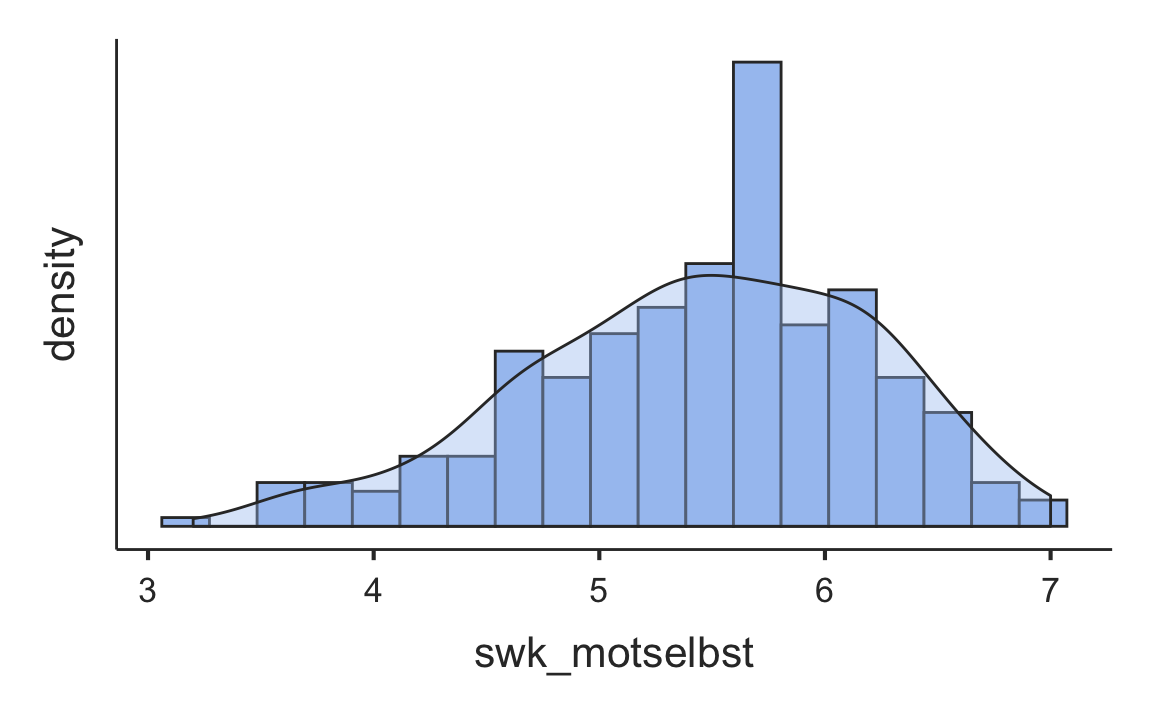
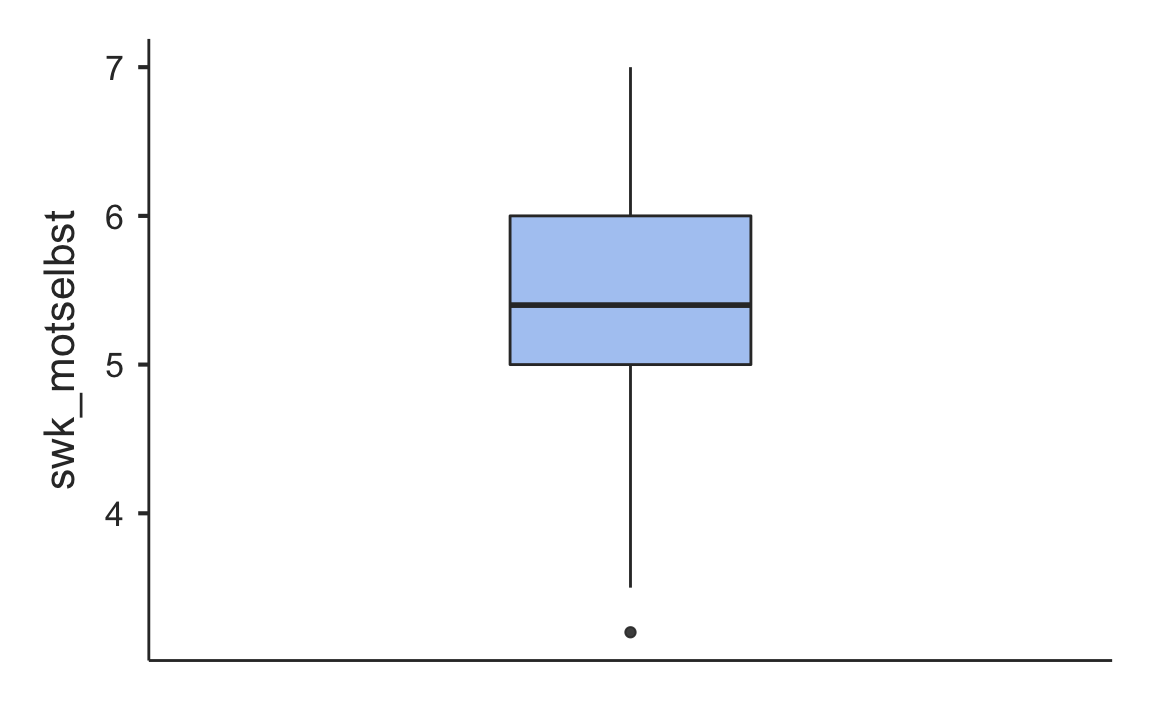
Some of the functionality of the jamovi program comes in modules. The functions in these modules are not included in the jmv package, but in additional packages like scatr.
A scatter plot can be obtained with scatr::scat().
library(scatr)
scat(
data = swk,
x = "swk_akad",
y = "swk_selbstreg",
group = "geschlecht",
line = "linear")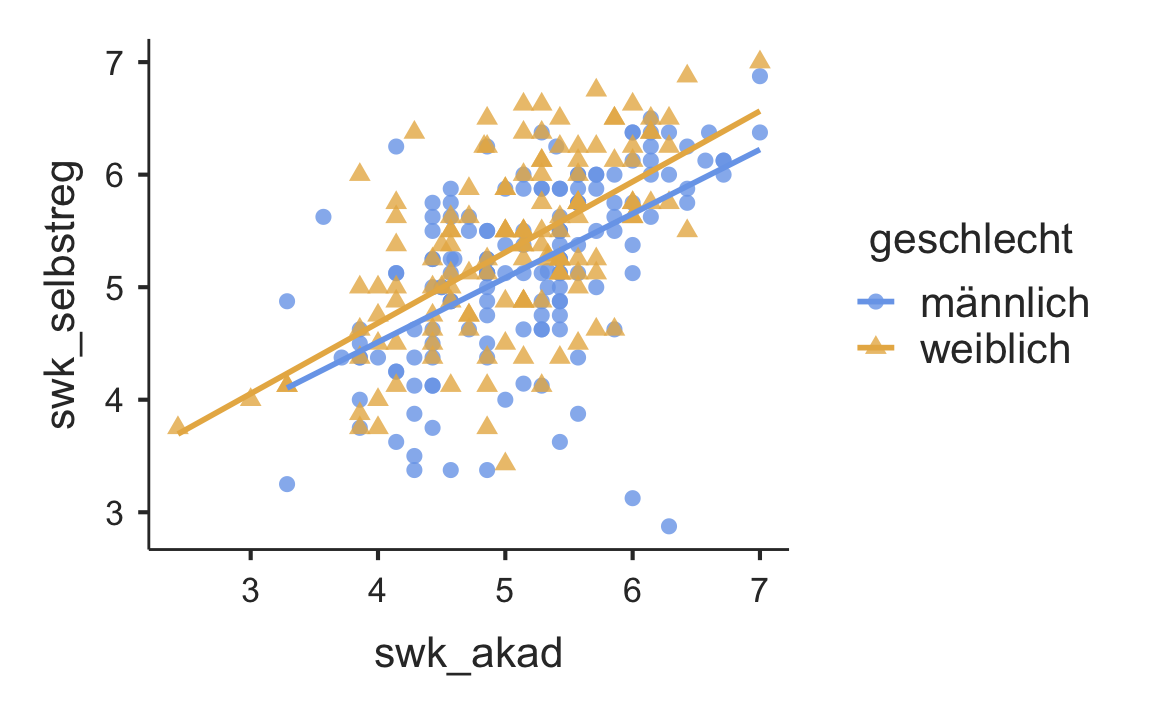
An overview of the available arguments is provided by ?scatr::scat:
scat(data, x, y, group = NULL, marg = "none", line = "none", se = FALSE)
Arguments
data the data as a data frame
x a string naming the variable from data that contains the x coordinates
of the points in the plot, variable must be numeric
y a string naming the variable from data that contains the y coordinates
of the points in the plot, variable must be numeric
group a string naming the variable from data that represents the grouping variable
marg none (default), dens, or box, provide respectively no plots, density plots,
or box plots on the axes
line none (default), linear, or smooth, provide respectively no regression line,
a linear regression line, or a smoothed regression line
se TRUE or FALSE (default), show the standard error for the regression lineLet’s try some of these:
library(scatr)
scat(
data = swk,
x = "swk_akad",
y = "swk_selbstreg",
group = "geschlecht",
marg = "dens",
line = "smooth",
se = TRUE)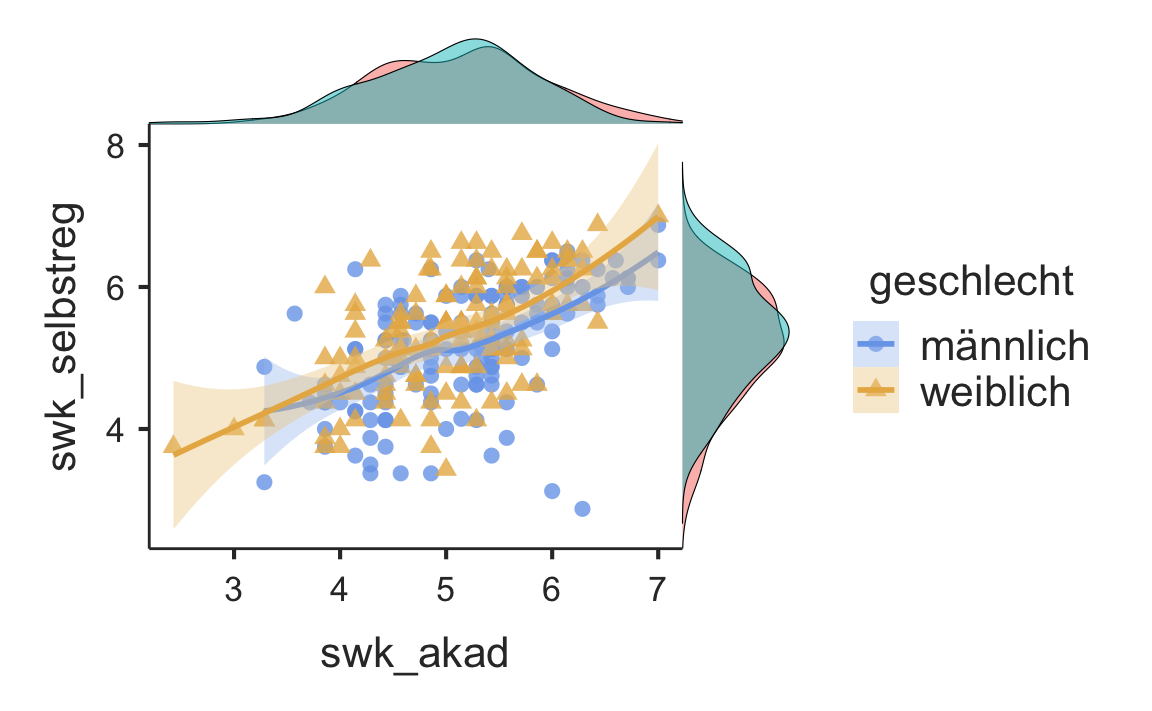
7.5 Correlations
7.5.1 Traditional ways of doing correlations in R
The generic form for calculating a (Pearson) correlation matrix using base R is as follows: cor(df[,c("var1", "var2", "var3")], methdod = c("pearson", "kendall", "spearman"), use = "complete.obs"). We can thus compute Pearson correlations (default) or - for ordinal data - Kendall’s tau or Spearman rank correlations.
swk_cor <- swk %>%
select(-geschlecht) %>%
cor(method = "pearson", use = "complete.obs") %>%
round(3)
swk_cor
#> swk_akad swk_selbstreg swk_durch swk_motselbst swk_sozharm
#> swk_akad 1.000 0.562 0.351 0.640 0.363
#> swk_selbstreg 0.562 1.000 0.318 0.724 0.342
#> swk_durch 0.351 0.318 1.000 0.415 0.592
#> swk_motselbst 0.640 0.724 0.415 1.000 0.407
#> swk_sozharm 0.363 0.342 0.592 0.407 1.000
#> swk_bez 0.392 0.466 0.327 0.415 0.493
#> swk_bez
#> swk_akad 0.392
#> swk_selbstreg 0.466
#> swk_durch 0.327
#> swk_motselbst 0.415
#> swk_sozharm 0.493
#> swk_bez 1.000
If we want covariances instead of correlations we can use cov() with the same arguments as cor(): cov(df[,c(“var1”, “var2”, “var3”)], methdod = c(“pearson”, “kendall”, “spearman”), use = “complete.obs”).
A good way to display a scatterplot matrix for a number of variables is the function scatterplotMatrix from the car package. In addition to displaying all combinations of bivariate scatterplots it is possible to get different univariate plots in the diagonal: diagonal = c("density","boxplot","histogram","oned","qqplot","none"). Similar to scat() above, smooth = TRUE can be used to display a non-linear LOWESS line (LOcally WEighted Scatterplot Smoother) to assess the (non-)linearity of the correlation.
library(car)
scatterplotMatrix(~ swk_akad + swk_selbstreg + swk_sozharm + swk_durch,
smooth = TRUE,
diagonal = "density",
data = swk)
#> Warning in applyDefaults(diagonal, defaults = list(method =
#> "adaptiveDensity"), : unnamed diag arguments, will be ignored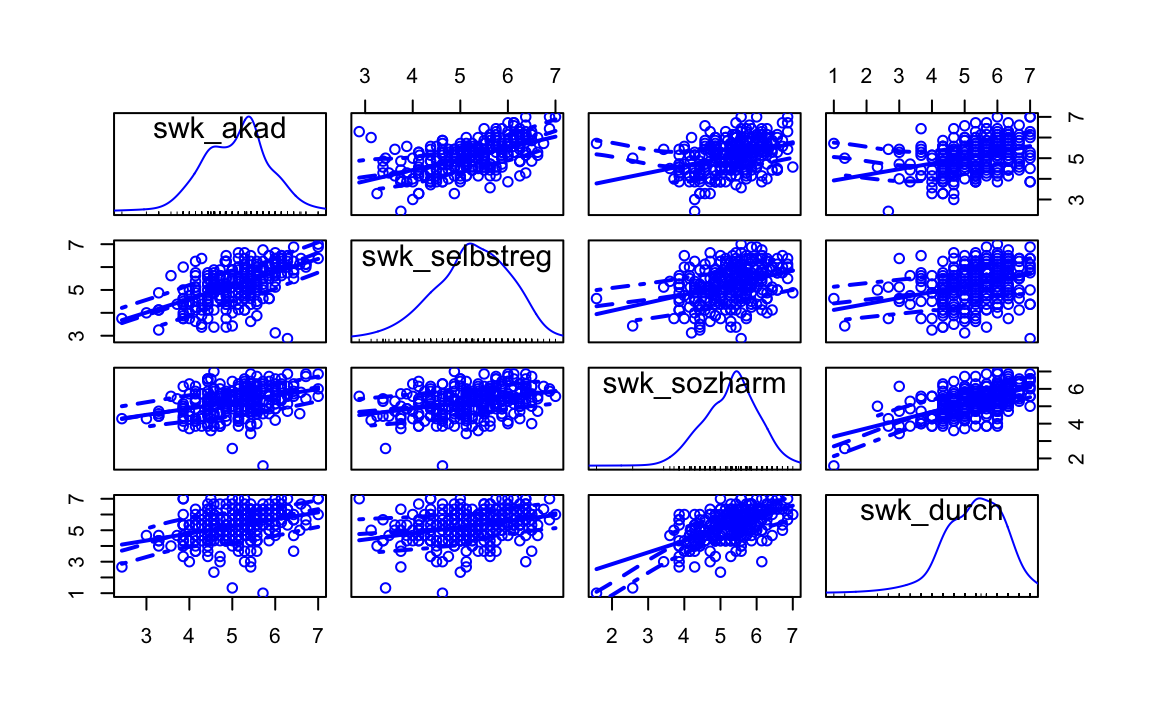
The function cor.test() can do a significance test for correlations, but only one at a time. The generic form is: cor. test (x, y, alternative = c ("two. sided", "less", "greater"), method = c ("pearson", "kendall", "spearman"), conf. level = 0.95). In addition to the non-directional alternative hypothesis (alternative = "two.sided"), we can also test directional alternative hypotheses: (alternative = "less") for a hypothesized negative correlation (“less than 0”) and (alternative = "greater") for a hypothesized positive correlation (“greater than 0”).
cor.test(swk$swk_akad, swk$swk_sozharm, alternative = "greater", method = "pearson")
#>
#> Pearson's product-moment correlation
#>
#> data: swk$swk_akad and swk$swk_sozharm
#> t = 6.5528, df = 284, p-value = 1.325e-10
#> alternative hypothesis: true correlation is greater than 0
#> 95 percent confidence interval:
#> 0.2746381 1.0000000
#> sample estimates:
#> cor
#> 0.3624033p <- swk %>%
select(swk_akad, swk_sozharm) %>%
drop_na() %>%
ggplot(mapping = aes(x = swk_akad,
y = swk_sozharm))
p + geom_jitter(size = 3, alpha = 0.6) +
stat_smooth(method = "lm", se = TRUE) +
theme_classic()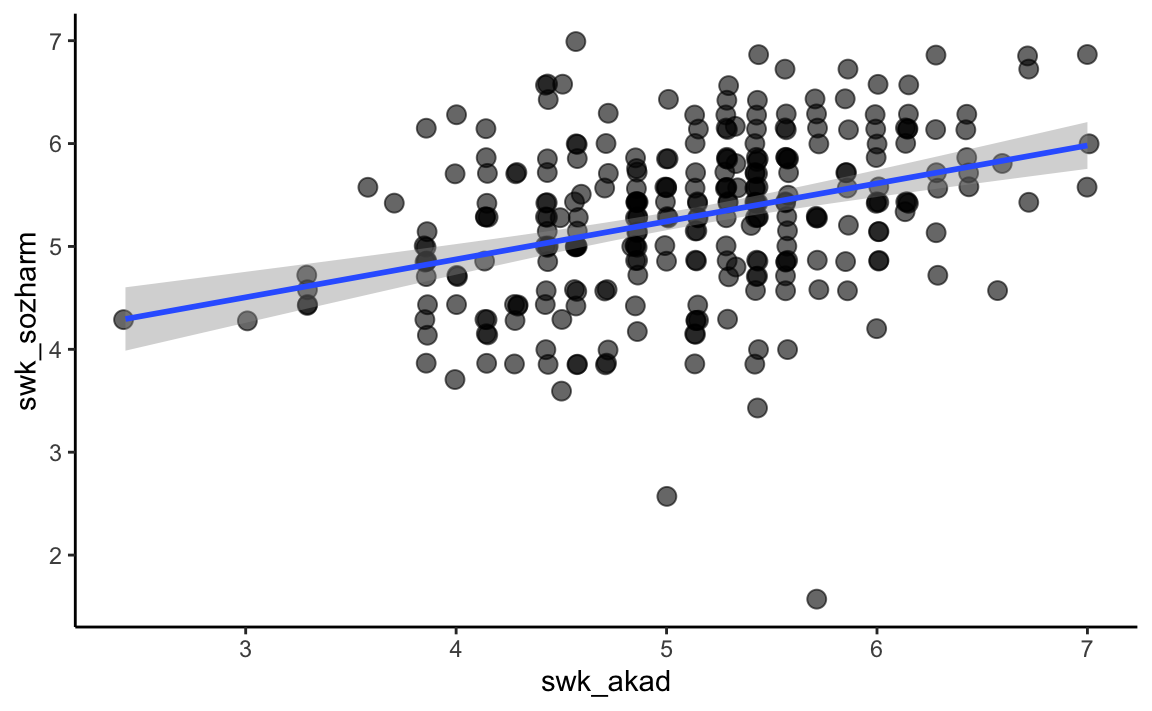
The function corr.test() from the psych package returns p-values for a correlation matrix. However, no directional alternative hypotheses are possible here. Matrices of correlations, sample sizes and p-values are displayed. With the p-value matrix, note that the unadjusted (two-sided) p-values are in the lower triangular matrix and the p-values adjusted according to Holm are in the upper triangular matrix. The Holm procedure corresponds to a sequential alpha correction that is less conservative than the Bonferroni procedure, but nevertheless controls the family-wise error. In the diagonals we also obtain p-values for the variances of the variables!
In the Holm procedure (Bonferroni-Holm method), the smallest p-value is multiplied by the number of tests (\(p(p-1)/2\); p = number of variables in the correlation matrix), the second smallest by the number of tests minus 1, etc. until the largest p-value that is no longer corrected (i.e., multiplied by \(p-p+1 = 1\)). However, the p-value is only multiplied by the corresponding number of tests if the resulting adjusted p-value is not smaller than the previously adjusted (smaller) p-value. If this is the case, the test is assigned the same p-value as its predecessor. This prevents that a smaller effect gets a smaller p-value after the adjustment than a larger effect, thereby preventing that a smaller effect may reach significance while the larger effect does not.
library(psych)
swk[1:25,] %>% select(starts_with("swk")) %>%
corr.test()
#> Call:corr.test(x = .)
#> Correlation matrix
#> swk_akad swk_selbstreg swk_durch swk_motselbst swk_sozharm
#> swk_akad 1.00 0.38 0.66 0.45 0.55
#> swk_selbstreg 0.38 1.00 0.47 0.70 0.37
#> swk_durch 0.66 0.47 1.00 0.41 0.72
#> swk_motselbst 0.45 0.70 0.41 1.00 0.49
#> swk_sozharm 0.55 0.37 0.72 0.49 1.00
#> swk_bez 0.31 0.56 0.34 0.66 0.66
#> swk_bez
#> swk_akad 0.31
#> swk_selbstreg 0.56
#> swk_durch 0.34
#> swk_motselbst 0.66
#> swk_sozharm 0.66
#> swk_bez 1.00
#> Sample Size
#> [1] 25
#> Probability values (Entries above the diagonal are adjusted for multiple tests.)
#> swk_akad swk_selbstreg swk_durch swk_motselbst swk_sozharm
#> swk_akad 0.00 0.23 0.00 0.14 0.04
#> swk_selbstreg 0.06 0.00 0.12 0.00 0.23
#> swk_durch 0.00 0.02 0.00 0.21 0.00
#> swk_motselbst 0.02 0.00 0.04 0.00 0.11
#> swk_sozharm 0.00 0.07 0.00 0.01 0.00
#> swk_bez 0.13 0.00 0.09 0.00 0.00
#> swk_bez
#> swk_akad 0.23
#> swk_selbstreg 0.04
#> swk_durch 0.23
#> swk_motselbst 0.00
#> swk_sozharm 0.00
#> swk_bez 0.00
#>
#> To see confidence intervals of the correlations, print with the short=FALSE option7.5.2 Partial correlation
Partial correlations can be obtained partial.cor(df[, c("var1", "var2", "var3")], use = "complete.obs"). Important: Partialling for the corresponding bivariate correlation is done for all other variables in the data frame!
# Normal correlation matrix for comparison (zero-order correlations)
cor(westost_scales[,c("swk_akad", "swk_selbstreg", "Schnitt", "leben_schule")],
use = "complete.obs")
#> swk_akad swk_selbstreg Schnitt leben_schule
#> swk_akad 1.0000000 0.5603931 0.4168517 0.3902735
#> swk_selbstreg 0.5603931 1.0000000 0.3824271 0.4896185
#> Schnitt 0.4168517 0.3824271 1.0000000 0.4754183
#> leben_schule 0.3902735 0.4896185 0.4754183 1.0000000
# Partial correlation matrix with three variables (first-order partial correlations)
partial.cor(westost_scales[,c("swk_akad", "swk_selbstreg", "Schnitt")],
use = "complete.obs")
#>
#> Partial correlations:
#> swk_akad swk_selbstreg Schnitt
#> swk_akad 0.00000 0.47894 0.26472
#> swk_selbstreg 0.47894 0.00000 0.19889
#> Schnitt 0.26472 0.19889 0.00000
#>
#> Number of observations: 280
# Partial correlation matrix with four variables (second-order partial correlations)
partial.cor(westost_scales[,c("swk_akad", "swk_selbstreg",
"Schnitt", "leben_schule")],
use = "complete.obs")
#>
#> Partial correlations:
#> swk_akad swk_selbstreg Schnitt leben_schule
#> swk_akad 0.00000 0.43015 0.22486 0.07308
#> swk_selbstreg 0.43015 0.00000 0.07488 0.30949
#> Schnitt 0.22486 0.07488 0.00000 0.33116
#> leben_schule 0.07308 0.30949 0.33116 0.00000
#>
#> Number of observations: 2797.5.3 Correlation analysis with jmv
Almost all we have done above with the more traditional R functions we can also do in jmv using the corrMatrix() function:
library(jmv)
corrMatrix(
data = swk,
vars = c(
"swk_akad",
"swk_selbstreg",
"swk_motselbst",
"swk_durch",
"swk_sozharm",
"swk_bez"))
#>
#> CORRELATION MATRIX
#>
#> Correlation Matrix
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> swk_akad swk_selbstreg swk_motselbst swk_durch swk_sozharm swk_bez
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────
#> swk_akad Pearson's r — 0.562 0.641 0.351 0.362 0.391
#> p-value — < .001 < .001 < .001 < .001 < .001
#>
#> swk_selbstreg Pearson's r — 0.723 0.318 0.341 0.464
#> p-value — < .001 < .001 < .001 < .001
#>
#> swk_motselbst Pearson's r — 0.415 0.407 0.414
#> p-value — < .001 < .001 < .001
#>
#> swk_durch Pearson's r — 0.592 0.327
#> p-value — < .001 < .001
#>
#> swk_sozharm Pearson's r — 0.493
#> p-value — < .001
#>
#> swk_bez Pearson's r —
#> p-value —
#> ─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────An overview of the available arguments is provided by ?jmv::corrMatrix:
corrMatrix(data, vars, pearson = TRUE, spearman = FALSE, kendall = FALSE,
sig = TRUE, flag = FALSE, ci = FALSE, ciWidth = 95, plots = FALSE,
plotDens = FALSE, plotStats = FALSE, hypothesis = "corr")
Arguments
data the data as a data frame
vars a vector of strings naming the variables to correlate in data
pearson TRUE (default) or FALSE, provide Pearson's R
spearman TRUE or FALSE (default), provide Spearman's rho
kendall TRUE or FALSE (default), provide Kendall's tau-b
sig TRUE (default) or FALSE, provide significance levels
flag TRUE or FALSE (default), flag significant correlations
ci TRUE or FALSE (default), provide confidence intervals
ciWidth a number between 50 and 99.9 (default: 95), the width of CI
plots TRUE or FALSE (default), provide a correlation matrix plot
plotDens TRUE or FALSE (default), provide densities in the correlation matrix plot
plotStats TRUE or FALSE (default), provide statistics in the correlation matrix plot
hypothesis one of 'corr' (default), 'pos', 'neg' specifying the alernative hypothesis;
correlated, correlated positively, correlated negatively respectively.Let’s try some options with only the three academic self-efficacy variables:
corrMatrix(
data = swk,
vars = c(
"swk_akad",
"swk_selbstreg",
"swk_motselbst"),
kendall = TRUE,
sig = FALSE,
flag = TRUE,
ci = TRUE)
#>
#> CORRELATION MATRIX
#>
#> Correlation Matrix
#> ──────────────────────────────────────────────────────────────────────────────────
#> swk_akad swk_selbstreg swk_motselbst
#> ──────────────────────────────────────────────────────────────────────────────────
#> swk_akad Pearson's r — 0.562 0.641
#> 95% CI Upper — 0.636 0.704
#> 95% CI Lower — 0.477 0.567
#> Kendall's Tau B — 0.425 0.471
#>
#> swk_selbstreg Pearson's r — 0.723
#> 95% CI Upper — 0.774
#> 95% CI Lower — 0.663
#> Kendall's Tau B — 0.569
#>
#> swk_motselbst Pearson's r —
#> 95% CI Upper —
#> 95% CI Lower —
#> Kendall's Tau B —
#> ──────────────────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .0017.6 Reliability analysis
7.6.1 Reliability analysis using the psych package
For the reliability analysis we will need the data set containing all individual items (westost). Then we create two reduced data sets: One for the scale “Self-Efficacy: Academic Achievement” (swkakad) including items T1_1, T1_7, T1_14, T1_16, T1_26, T1_27, and T1_31. And another for the scale “Self-Efficacy: Social Harmony” (swksozharm) including items T1_2, T1_8, T1_15, T1_23, T1_29, T1_32, and T1_35.
library(psych)
load(file = "data/westost.Rdata")
names(westost)
#> [1] "ID" "westost" "geschlecht"
#> [4] "alter" "T1_1" "T1_2"
#> [7] "T1_3" "T1_4" "T1_5"
#> [10] "T1_6" "T1_7" "T1_8"
#> [13] "T1_9" "T1_10" "T1_11"
#> [16] "T1_12" "T1_13" "T1_14"
#> [19] "T1_15" "T1_16" "T1_17"
#> [22] "T1_18" "T1_19" "T1_20"
#> [25] "T1_21" "T1_22" "T1_23"
#> [28] "T1_24" "T1_25" "T1_26"
#> [31] "T1_27" "T1_28" "T1_29"
#> [34] "T1_30" "T1_31" "T1_32"
#> [37] "T1_33" "T1_34" "T1_35"
#> [40] "T1_36" "T2_1" "T2_2"
#> [43] "T2_3" "T2_4" "T2_5"
#> [46] "T2_6" "T3_1" "T3_2"
#> [49] "T3_3" "T3_4" "T3_5"
#> [52] "T3_6" "T4_1" "T4_2"
#> [55] "T4_3" "T4_4" "T4_5"
#> [58] "T4_6" "T4_7" "T4_8"
#> [61] "T4_9" "T4_10" "T4_11"
#> [64] "T5_1" "T5_2" "T5_3"
#> [67] "T5_4" "T5_5" "T5_6"
#> [70] "T5_7" "T5_8" "T5_9"
#> [73] "T5_10" "T5_11" "T6_1"
#> [76] "T6_2" "T6_3" "T6_4"
#> [79] "T6_5" "T6_6" "T6_7"
#> [82] "T6_8" "T6_9" "T6_10"
#> [85] "T6_11" "T7_1" "T7_2"
#> [88] "T7_3" "T7_4" "T7_5"
#> [91] "T7_6" "T7_7" "T7_8"
#> [94] "T7_9" "T7_10" "T7_11"
#> [97] "T7_12" "SES" "Deutsch"
#> [100] "Mathe" "Fremdspr" "Schnitt"
#> [103] "bildung_vater" "bildung_mutter" "bildung_vater_b"
#> [106] "bildung_mutter_b" "swk_akad" "swk_selbstreg"
#> [109] "swk_durch" "swk_motselbst" "swk_sozharm"
#> [112] "swk_bez" "unt_eltern" "unt_freunde"
#> [115] "sch_leistung" "sch_bez" "sch_regeln"
#> [118] "ges_gerecht" "ges_nepot" "leben_selbst"
#> [121] "leben_fam" "leben_schule" "leben_freunde"
#> [124] "leben_gesamt" "stress_somat" "stress_psych"
swkakad <- westost %>%
select(one_of(c("T1_1", "T1_7", "T1_14", "T1_16",
"T1_26", "T1_27", "T1_31")))
swkakad
#> # A tibble: 286 x 7
#> T1_1 T1_7 T1_14 T1_16 T1_26 T1_27 T1_31
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 4 5 5 7 5 4 5
#> 2 3 5 5 7 4 5 5
#> 3 4 1 2 6 6 5 4
#> 4 6 5 6 7 7 6 6
#> 5 5 5 4 6 6 4 6
#> 6 6 5 6 7 7 3 4
#> # … with 280 more rows
swksozharm <- westost %>%
select(one_of(c("T1_2", "T1_8", "T1_15", "T1_23",
"T1_29", "T1_32", "T1_35")))
swksozharm
#> # A tibble: 286 x 7
#> T1_2 T1_8 T1_15 T1_23 T1_29 T1_32 T1_35
#> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 6 6 5 5 5 6 6
#> 2 5 6 4 3 4 6 5
#> 3 3 6 4 3 3 5 7
#> 4 6 6 6 6 6 6 6
#> 5 3 4 3 4 4 6 5
#> 6 6 6 6 5 7 7 7
#> # … with 280 more rowsCronbach’s alpha
The internal consistency (Cronbach’s Alpha) can be computed using the function alpha():
alpha(swkakad)
#>
#> Reliability analysis
#> Call: alpha(x = swkakad)
#>
#> raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
#> 0.63 0.63 0.65 0.19 1.7 0.033 5.1 0.77 0.18
#>
#> lower alpha upper 95% confidence boundaries
#> 0.56 0.63 0.7
#>
#> Reliability if an item is dropped:
#> raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
#> T1_1 0.59 0.59 0.60 0.19 1.4 0.037 0.022 0.168
#> T1_7 0.58 0.58 0.57 0.19 1.4 0.039 0.013 0.192
#> T1_14 0.57 0.56 0.57 0.18 1.3 0.039 0.022 0.097
#> T1_16 0.64 0.64 0.65 0.23 1.8 0.032 0.020 0.192
#> T1_26 0.61 0.61 0.63 0.21 1.6 0.035 0.024 0.180
#> T1_27 0.58 0.58 0.59 0.19 1.4 0.039 0.021 0.168
#> T1_31 0.56 0.57 0.56 0.18 1.3 0.040 0.015 0.180
#>
#> Item statistics
#> n raw.r std.r r.cor r.drop mean sd
#> T1_1 286 0.53 0.56 0.45 0.34 5.0 1.2
#> T1_7 284 0.61 0.58 0.52 0.39 5.0 1.5
#> T1_14 283 0.61 0.62 0.54 0.41 4.9 1.4
#> T1_16 285 0.43 0.43 0.24 0.18 5.8 1.4
#> T1_26 285 0.47 0.50 0.34 0.27 5.3 1.2
#> T1_27 281 0.61 0.58 0.48 0.38 4.9 1.5
#> T1_31 283 0.63 0.61 0.56 0.43 4.7 1.4
#>
#> Non missing response frequency for each item
#> 1 2 3 4 5 6 7 miss
#> T1_1 0.01 0.01 0.07 0.20 0.33 0.30 0.08 0.00
#> T1_7 0.02 0.04 0.12 0.13 0.29 0.24 0.16 0.01
#> T1_14 0.03 0.05 0.07 0.19 0.26 0.32 0.10 0.01
#> T1_16 0.02 0.02 0.03 0.09 0.15 0.32 0.36 0.00
#> T1_26 0.01 0.01 0.05 0.14 0.31 0.33 0.15 0.00
#> T1_27 0.04 0.03 0.09 0.21 0.23 0.26 0.15 0.02
#> T1_31 0.03 0.03 0.13 0.22 0.26 0.23 0.10 0.01Optionally, a “key vector” can be defined. This is particularly useful if you have some items that have been formulated in the opposite direction and therefore should actually be recoded before doing the reliability analysis. The “key vector” indicates which items have to be recoded (here: none!)
alpha(swkakad, keys = c(1, 1, 1, 1, 1, 1, 1))
#>
#> Reliability analysis
#> Call: alpha(x = swkakad, keys = c(1, 1, 1, 1, 1, 1, 1))
#>
#> raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
#> 0.63 0.63 0.65 0.19 1.7 0.033 5.1 0.77 0.18
#>
#> lower alpha upper 95% confidence boundaries
#> 0.56 0.63 0.7
#>
#> Reliability if an item is dropped:
#> raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
#> T1_1 0.59 0.59 0.60 0.19 1.4 0.037 0.022 0.168
#> T1_7 0.58 0.58 0.57 0.19 1.4 0.039 0.013 0.192
#> T1_14 0.57 0.56 0.57 0.18 1.3 0.039 0.022 0.097
#> T1_16 0.64 0.64 0.65 0.23 1.8 0.032 0.020 0.192
#> T1_26 0.61 0.61 0.63 0.21 1.6 0.035 0.024 0.180
#> T1_27 0.58 0.58 0.59 0.19 1.4 0.039 0.021 0.168
#> T1_31 0.56 0.57 0.56 0.18 1.3 0.040 0.015 0.180
#>
#> Item statistics
#> n raw.r std.r r.cor r.drop mean sd
#> T1_1 286 0.53 0.56 0.45 0.34 5.0 1.2
#> T1_7 284 0.61 0.58 0.52 0.39 5.0 1.5
#> T1_14 283 0.61 0.62 0.54 0.41 4.9 1.4
#> T1_16 285 0.43 0.43 0.24 0.18 5.8 1.4
#> T1_26 285 0.47 0.50 0.34 0.27 5.3 1.2
#> T1_27 281 0.61 0.58 0.48 0.38 4.9 1.5
#> T1_31 283 0.63 0.61 0.56 0.43 4.7 1.4
#>
#> Non missing response frequency for each item
#> 1 2 3 4 5 6 7 miss
#> T1_1 0.01 0.01 0.07 0.20 0.33 0.30 0.08 0.00
#> T1_7 0.02 0.04 0.12 0.13 0.29 0.24 0.16 0.01
#> T1_14 0.03 0.05 0.07 0.19 0.26 0.32 0.10 0.01
#> T1_16 0.02 0.02 0.03 0.09 0.15 0.32 0.36 0.00
#> T1_26 0.01 0.01 0.05 0.14 0.31 0.33 0.15 0.00
#> T1_27 0.04 0.03 0.09 0.21 0.23 0.26 0.15 0.02
#> T1_31 0.03 0.03 0.13 0.22 0.26 0.23 0.10 0.01The following command is (erroneously) specified with recoding keys on variables 2 and 5:
alpha(swkakad, keys = c(1, -1, 1, 1, -1, 1, 1))
#>
#> Reliability analysis
#> Call: alpha(x = swkakad, keys = c(1, -1, 1, 1, -1, 1, 1))
#>
#> raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
#> 0.63 0.63 0.65 0.19 1.7 0.033 5.1 0.77 0.18
#>
#> lower alpha upper 95% confidence boundaries
#> 0.56 0.63 0.7
#>
#> Reliability if an item is dropped:
#> raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
#> T1_1 0.59 0.59 0.60 0.19 1.4 0.037 0.022 0.168
#> T1_7 0.58 0.58 0.57 0.19 1.4 0.039 0.013 0.192
#> T1_14 0.57 0.56 0.57 0.18 1.3 0.039 0.022 0.097
#> T1_16 0.64 0.64 0.65 0.23 1.8 0.032 0.020 0.192
#> T1_26 0.61 0.61 0.63 0.21 1.6 0.035 0.024 0.180
#> T1_27 0.58 0.58 0.59 0.19 1.4 0.039 0.021 0.168
#> T1_31 0.56 0.57 0.56 0.18 1.3 0.040 0.015 0.180
#>
#> Item statistics
#> n raw.r std.r r.cor r.drop mean sd
#> T1_1 286 0.53 0.56 0.45 0.34 5.0 1.2
#> T1_7 284 0.61 0.58 0.52 0.39 5.0 1.5
#> T1_14 283 0.61 0.62 0.54 0.41 4.9 1.4
#> T1_16 285 0.43 0.43 0.24 0.18 5.8 1.4
#> T1_26 285 0.47 0.50 0.34 0.27 5.3 1.2
#> T1_27 281 0.61 0.58 0.48 0.38 4.9 1.5
#> T1_31 283 0.63 0.61 0.56 0.43 4.7 1.4
#>
#> Non missing response frequency for each item
#> 1 2 3 4 5 6 7 miss
#> T1_1 0.01 0.01 0.07 0.20 0.33 0.30 0.08 0.00
#> T1_7 0.02 0.04 0.12 0.13 0.29 0.24 0.16 0.01
#> T1_14 0.03 0.05 0.07 0.19 0.26 0.32 0.10 0.01
#> T1_16 0.02 0.02 0.03 0.09 0.15 0.32 0.36 0.00
#> T1_26 0.01 0.01 0.05 0.14 0.31 0.33 0.15 0.00
#> T1_27 0.04 0.03 0.09 0.21 0.23 0.26 0.15 0.02
#> T1_31 0.03 0.03 0.13 0.22 0.26 0.23 0.10 0.01Explanation of the output:
raw_alpha # (Normal) Alpha based on covariances
std.alpha # Standardized Alpha based on correlations
G6(smc) # Guttman's Lambda 6 (alternative measure of reliability)
average_r # Average inter-item-correlation
mean # Scale mean (across all items)
sd # Scale standard deviation
alpha.drop # Statistics in case the respective item is deleted from the scale
item.stats # Item-total correlations (for raw and corrected scores) alpha(swksozharm)
#>
#> Reliability analysis
#> Call: alpha(x = swksozharm)
#>
#> raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
#> 0.8 0.82 0.81 0.39 4.5 0.018 5.3 0.78 0.36
#>
#> lower alpha upper 95% confidence boundaries
#> 0.77 0.8 0.84
#>
#> Reliability if an item is dropped:
#> raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
#> T1_2 0.76 0.78 0.76 0.37 3.5 0.022 0.011 0.32
#> T1_8 0.76 0.78 0.76 0.37 3.5 0.022 0.012 0.32
#> T1_15 0.79 0.80 0.79 0.41 4.1 0.020 0.017 0.37
#> T1_23 0.82 0.82 0.81 0.44 4.6 0.016 0.011 0.39
#> T1_29 0.78 0.80 0.79 0.40 4.1 0.020 0.018 0.35
#> T1_32 0.77 0.78 0.77 0.37 3.5 0.022 0.013 0.35
#> T1_35 0.77 0.78 0.76 0.37 3.6 0.022 0.011 0.36
#>
#> Item statistics
#> n raw.r std.r r.cor r.drop mean sd
#> T1_2 285 0.75 0.75 0.71 0.61 5.2 1.27
#> T1_8 281 0.75 0.76 0.71 0.63 5.5 1.10
#> T1_15 284 0.64 0.64 0.54 0.49 4.7 1.10
#> T1_23 278 0.60 0.55 0.42 0.37 4.5 1.47
#> T1_29 286 0.65 0.65 0.56 0.51 5.1 1.10
#> T1_32 281 0.73 0.75 0.70 0.62 5.8 0.99
#> T1_35 281 0.72 0.75 0.71 0.62 6.1 0.96
#>
#> Non missing response frequency for each item
#> 1 2 3 4 5 6 7 miss
#> T1_2 0.01 0.01 0.07 0.20 0.27 0.27 0.17 0.00
#> T1_8 0.00 0.01 0.02 0.15 0.26 0.39 0.17 0.02
#> T1_15 0.01 0.01 0.07 0.30 0.38 0.17 0.05 0.01
#> T1_23 0.04 0.06 0.12 0.24 0.27 0.20 0.08 0.03
#> T1_29 0.00 0.01 0.06 0.20 0.36 0.27 0.10 0.00
#> T1_32 0.01 0.00 0.01 0.05 0.25 0.44 0.23 0.02
#> T1_35 0.00 0.00 0.01 0.04 0.18 0.39 0.38 0.02Via the summary() function it is also possible obtain only alpha. To do this, the result of the analysis must be saved in an object:
sozharm_rel <- alpha(swksozharm)
summary(sozharm_rel)
#>
#> Reliability analysis
#> raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
#> 0.8 0.82 0.81 0.39 4.5 0.018 5.3 0.78 0.36
# also possible:
swksozharm %>%
alpha() %>%
summary()
#>
#> Reliability analysis
#> raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
#> 0.8 0.82 0.81 0.39 4.5 0.018 5.3 0.78 0.367.6.2 Reliability analysis with jmv
library(jmv)
reliability(
data = westost,
vars = c(
"T1_1",
"T1_7",
"T1_14",
"T1_16",
"T1_26",
"T1_27",
"T1_31"),
omegaScale = TRUE,
meanScale = TRUE,
sdScale = TRUE,
corPlot = TRUE,
alphaItems = TRUE,
omegaItems = TRUE,
meanItems = TRUE,
sdItems = TRUE,
itemRestCor = TRUE)
#>
#> RELIABILITY ANALYSIS
#>
#> Scale Reliability Statistics
#> ──────────────────────────────────────────────────────────
#> mean sd Cronbach's α McDonald's ω
#> ──────────────────────────────────────────────────────────
#> scale 5.10 0.777 0.637 0.643
#> ──────────────────────────────────────────────────────────
#>
#>
#> Item Reliability Statistics
#> ──────────────────────────────────────────────────────────────────────────────────
#> mean sd item-rest correlation Cronbach's α McDonald's ω
#> ──────────────────────────────────────────────────────────────────────────────────
#> T1_1 5.05 1.18 0.352 0.601 0.615
#> T1_7 4.99 1.49 0.390 0.586 0.601
#> T1_14 4.94 1.44 0.418 0.577 0.597
#> T1_16 5.75 1.41 0.195 0.648 0.650
#> T1_26 5.30 1.20 0.271 0.622 0.634
#> T1_27 4.92 1.51 0.385 0.588 0.598
#> T1_31 4.75 1.42 0.431 0.573 0.589
#> ──────────────────────────────────────────────────────────────────────────────────
# revItems = "")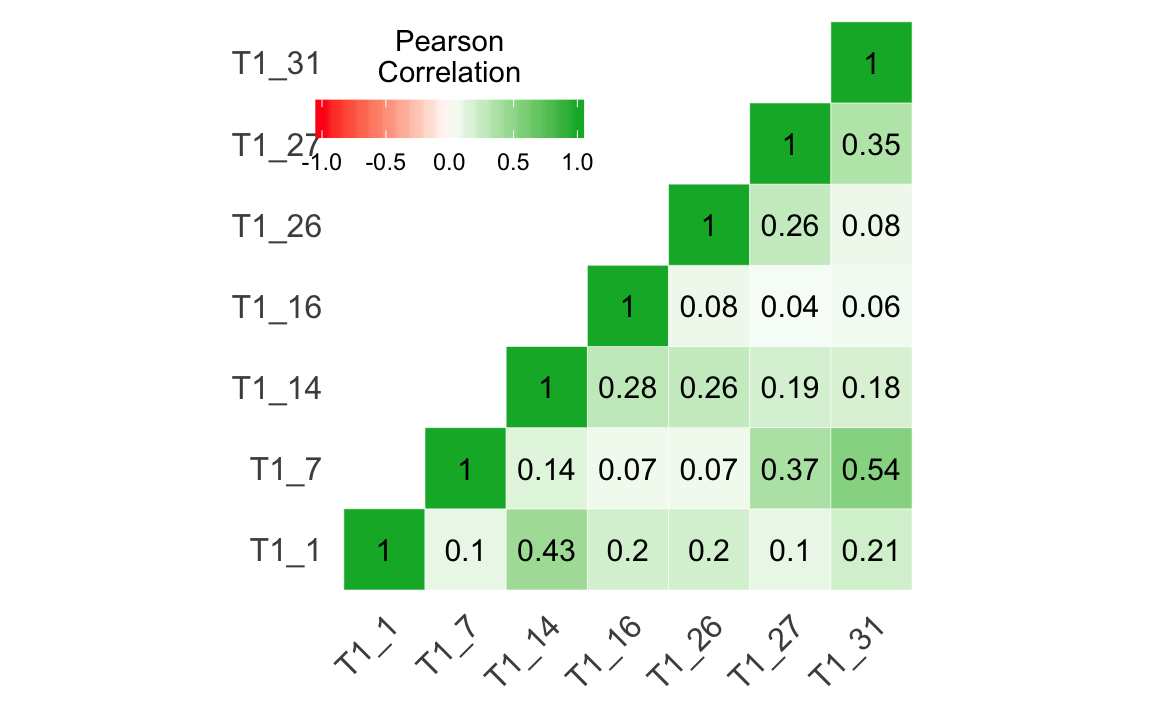
library(jmv)
reliability(
data = westost,
vars = c(
"T1_2",
"T1_8",
"T1_15",
"T1_23",
"T1_29",
"T1_32",
"T1_35"),
omegaScale = TRUE,
meanScale = TRUE,
sdScale = TRUE,
corPlot = TRUE,
alphaItems = TRUE,
omegaItems = TRUE,
meanItems = TRUE,
sdItems = TRUE,
itemRestCor = TRUE,
revItems = "T1_2")
#>
#> RELIABILITY ANALYSIS
#>
#> Scale Reliability Statistics
#> ──────────────────────────────────────────────────────────
#> mean sd Cronbach's α McDonald's ω
#> ──────────────────────────────────────────────────────────
#> scale 4.93 0.568 0.475 0.676
#> ──────────────────────────────────────────────────────────
#> Note. item 'T1_2' correlates negatively with the
#> total scale and probably should be reversed
#>
#>
#> Item Reliability Statistics
#> ─────────────────────────────────────────────────────────────────────────────────────
#> mean sd item-rest correlation Cronbach's α McDonald's ω
#> ─────────────────────────────────────────────────────────────────────────────────────
#> T1_2 ᵃ 2.80 1.262 -0.606 0.762 0.783
#> T1_8 5.50 1.098 0.467 0.323 0.579
#> T1_15 4.72 1.117 0.441 0.334 0.625
#> T1_23 4.55 1.487 0.386 0.339 0.649
#> T1_29 5.12 1.084 0.450 0.333 0.621
#> T1_32 5.77 1.000 0.485 0.328 0.579
#> T1_35 6.08 0.963 0.451 0.348 0.589
#> ─────────────────────────────────────────────────────────────────────────────────────
#> ᵃ reverse scaled item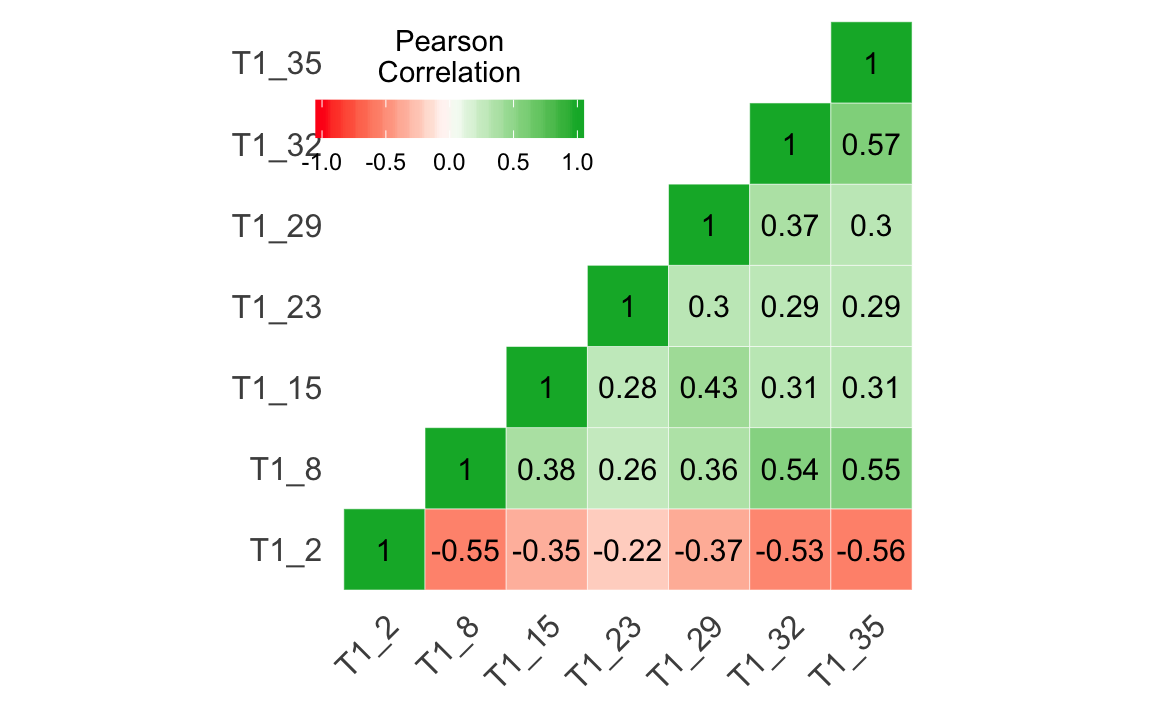
prop.table()uses as first argument a cross table as produced bytable(). Only if we use it with the pipe%>%we can use the unnamed value for the margin argument as presented above.